бинарный код десятичный код
Двоично-десятичное кодирование
Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот.
После калькулятора Перевод дробных чисел из одной системы счисления в другую я думал, что тема с системами счисления уже закрыта. Но, как оказалось, еще нет.
Как я писал по ссылке выше, основная проблема при переводе дробных чисел из одной системы счисления в другую это потеря точности, когда, например, десятичное число 0.8 нельзя перевести в двоичное без погрешности.
Поскольку десятичные числа активно используются человеком, а двоичные — компьютером, этой проблемой в применении к двоичной и десятичной системам однажды уже озаботились какие-то светлые умы и придумали двоично-десятичное кодирование (binary coded decimal, BCD). Суть идеи проста — берем и для каждой десятичной цифры заводим байт. И в этом байте тупо пишем значение десятичной цифры в двоичном коде. Тогда число, например, 0.8 будет 0.00001000. Потом, правда, подумали еще, и решили, что раз уж верхняя часть байта всегда пустует (так как максимум 9 — это 1001), то давайте для каждой десятичной цифры заводить полубайт. И назвали это упакованным двоично-десятичным кодированием (packed BCD).
В упакованном кодировании наше 0.8 будет 0.1000, а какое-нибудь 6.75 будет 0110.01110101.
Прекрасная идея, конечно. Точность не теряется, человек может двоичные числа переводить в десятичные и наоборот прямо на лету, округлять можно, откидывая лишнее. Но как-то не получила она широкого распространения, потому как жизнь машинам она, наоборот, усложняла — и памяти для хранения чисел надо больше, и операции над числами реализовать сложнее. Так и осталась забавным курьезом, и я бы ничего о ней не знал, если бы пользователи не подсказали, что есть такая.
Ну и небольшой калькулятор по этому поводу — вводим либо десятичное число, либо двоичное, подразумевая, что это упакованный двоично-десятичный код, и получаем результат. Понятно, что все преобразования можно проделать и в уме, и в этом ее преимущество; но зачем же лишний раз мозги напрягать, верно?
Запись десятичных чисел (двоично-десятичный код)
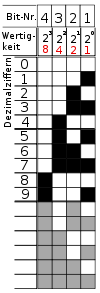
Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Не нужно путать двоично-десятичный код с десятичной системой счисления. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:
| Двоично-десятичный код | Десятичный код | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 0 | 0 | 0 | 8 |
| 1 | 0 | 0 | 1 | 9 |
Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:
В первой тетраде записана цифра 1, во второй — 2, в третьей — 5, а в последней тетраде записана цифра 8. В данном примере для записи числа 1258 потребовалось четыре тетрады. Количество ячеек памяти микропроцессора зависит от его разрядности. При 16-разрядном процессоре все число уместится в одну ячейку памяти.
В данном примере для записи числа достаточно трех тетрад, но ячейка памяти 16-разрядная. Поэтому старшая тетрада заполняется нулями. Они не изменяют значение цифры. Если бы мы заполнили нулями младшую тетраду, то число увеличилось бы в десять раз!
При записи десятичных чисел часто требуется записывать знак числа и десятичную запятую (в англоязычных странах точку). Двоично-десятичный код часто применяется для набора телефонного номера или набора кодов телефонных служб. В этом случае кроме десятичных цифр часто применяются символы ‘*’ или ‘#’. Для записи этих символов в двоично-десятичном коде применяются запрещенные комбинации
| Двоично-десятичный код | Дополнительный символ | |||
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | * (звёздочка) |
| 1 | 0 | 1 | 1 | # (решётка) |
| 1 | 1 | 0 | 0 | + (плюс) |
| 1 | 1 | 0 | 1 | – (минус) |
| 1 | 1 | 1 | 0 | , (десятичная запятая) |
| 1 | 1 | 1 | 1 | Символ гашения |
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа. Запишем те же числа, что и в предыдущем примере в неупакованном двоично-десятичном коде для восьмиразрядного процессора:
Суммирование двоично-десятичных чисел.
Понравился материал? Поделись с друзьями!
Другие виды двоичных кодов:
Целочисленные двоичные коды Представление двоичных чисел в памяти компьютера или микроконтроллера
https://digteh.ru/proc/IntCod.php
Представление чисел в двоичном коде с плавающей запятой Стандартные форматы чисел с плавающей запятой для компьютеров и микроконтроллеров
https://digteh.ru/proc/float/
Запись текстов двоичным кодом Представление текстов в памяти компьютеров и микроконтроллеров
https://digteh.ru/proc/text/
Системы счисления В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления.
https://digteh.ru/digital/SysSchis.php
Предыдущие версии сайта:
http://neic.nsk.su/
Об авторе:
к.т.н., доц., Александр Владимирович Микушин
Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).
А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.
Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.
Десятичный код.
К примеру, десятичное число 31110 в двоичной системе счисления записано будет в двоичном коде так : 1 0011 01112, в двоично-десятичном коде оно будет записано как 0001 0001BCD.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
В формате BCD из Unsigned Integer простой способ получения данных такой:
Число «A» в формате U16 = 542,
теперь, выполнив преобразование его в BCD (проделать операцию можно на калькуляторе ОС Windows) получаем :
Особенности десятичного кода.
Из преимуществ двоично-десятичного кода можно выделить такие:
— Упрощены операции умножения или деления на 10, а также округление.
Учитывая все эти преимущества, формат двоично-десятичного кода применяется в калькуляторах, ведь в простейших арифметических операциях, калькулятор должен в точности такой же самый выводить результат, какой человек подсчитает на бумаге.
Кроме достоинств, двоично-десятичный код имеет и свои характерные недостатки: требуется больше памяти и усложнены арифметические операции. Так как, вместо 16 в в 8421-BCD используются только 10 возможных комбинаций 4-х битового поля, поэтому при операциях сложения и вычитания чисел в формате 8421-BCD действуют такие правила:
— Каждый раз при сложении двоично-десятичных чисел, когда в старший полубайт происходит перенос бита, необходимо добавить корректирующее значение 0110 (= 610 = 1610 — 1010: разница количеств используемых значений и комбинаций полубайта) к тому полубайту, от которого был произведен перенос.
— Когда встречается комбинация недопустимая для полубайта то необходимо добавить с разрешением переноса в старшие полубайты к каждой недопустимой комбинации корректирующее значение 0110, каждый раз при выполнении сложения двоично-десятичных чисел.
— Для каждого полубайта, который получил заем из старшего полубайта, при вычитании двоично-десятичных чисел, необходимо провести коррекцию, для этого нужно отнять значение 0110.
Операция по сложению двоично-десятичных чисел на примере выглядит так: Задача: Определить число A = D + C, где D = 3927, C = 4856
Решение: Числа D и C представим в виде двоично-десятичного кода:
1000 0111 1000 0011
Двоичные коды для десятичных цифр
В ряде случаев в вычислительной технике применяется не только двоичная, но и десятичная система счисления. Однако и в этом случае для представления десятичных цифр используется оборудование, разработанное для представления двоичных цифр. В этом случае говорят о двоично-десятичных кодах десятичных цифр.
Согласно формулы Хартли для представления 10 различных цифр требуется четыре бита информации:
а) Коды с избытком
Кроме рассмотренной системы кодирования достаточно широко используются также так называемые коды с избытком. Рассмотрим группу кодов “8421” с избытком”.
Код “8421” с избытком W” строится по следующим правилам:
При кодировании десятичной цифры, к ней вначале прибавляют W, и затем полученное число представляют как двоичное в коде “8421”.
Значение W может быть равным 1, 2, 3, 4, 5 или 6. При любом значении избытка W шесть из шестнадцати комбинаций останутся неиспользованными. Только для разных избытков эти значения будут разными.
Пример. Рассмотрим код “8421” с избытком 3”.
а)Представим цифру 8 в данном коде.
Вначале увеличим 8 на 3. Получится 11.
Затем запишем 11 в коде “8421”. Получится 1011.
Число 1011 и есть представление цифры 8 в данном коде.
б)Восстановим цифру, которая изображается комбинацией 0101.
Вначале представим десятичное число, рассматривая комбинацию 0101, как его изображение в коде “8421”. Получится число 5.
Затем вычтем из него (из 5) избыток 3. Получится 2.
Это и есть искомый ответ: Комбинация 0101 изображает десятичную цифру 2 в коде “8421” с избытком 3”.
в)Восстановим цифру, которая изображается комбинацией 1110.
Восстановим десятичное число. Получится 14.
Вычтем из него избыток 3. Получится 11.
Поскольку 11 не является десятичной цифрой (это двухразрядное десятичное число), делаем вывод, что комбинация 1110 не изображает никакой десятичной цифры и является запрещенной.
б) Код “2421”
Кроме кодов с естественными весами разрядов применяются и другие. Одним из широко известных кодов является позиционный код, построенный с использованием тетрады двоичных цифр, веса которых слева направо равны соответственно : 2, 4, 2 и 1.
Представим коды цифр в таблице:
| Цифра | Код “2421” | Цифра | Код “2421” |
| 0 | 0000 | 5 | 0101 или 1011 |
| 1 | 0001 | 6 | 0110 или 1100 |
| 2 | 0010 или 1000 | 7 | 0111 или 1101 |
| 3 | 0011 или 1001 | 8 | 1110 |
| 4 | 0100 или 1010 | 9 | 1111 |
Как видно из таблицы, ряд десятичных цифр могут быть представлены двумя не совпадающими двоичными комбинациями.
Например, комбинации 0100 и 0010 изображают цифру 2, комбинации 1010 и 0100 изображают цифру 4 и т.д. Отличительной особенностью данного кода является то, что в нем нет неиспользованных (запрещенных) комбинаций.
в) Код “2 из 5”
Данный код принадлежит к непозиционным кодам. Как и все непозиционные коды он определяется табличным способом. Его название отражает принцип построения кода: любая десятичная цифра представляется комбинацией из 5 двоичных цифр, в которой точно две цифры 1 и, следовательно, три цифры 0.
Представим таблицу одного из возможных вариантов для данного кода:
| Цифра | Код | Цифра | Код |
| 0 | 11000 | 5 | 01010 |
| 1 | 00011 | 6 | 01100 |
| 2 | 00101 | 7 | 10001 |
| 3 | 00110 | 8 | 10010 |
| 4 | 01001 | 9 | 10100 |
Все остальные возможные комбинации, в которых число единиц не равно двум, являются запрещенными.
Также как и все коды на основе тетрады “8421”, последний код принадлежит к группе кодов, обладающих так называемыми диагностическими возможностями: Если известно, что некоторая комбинация должна изображать десятичную цифру, но попадает в область запрещенных, значит произошло искажение информации. Это свойство кодов активно используется в аппаратуре ЭВМ.
Для закрепления материала по переводу чисел из одной системы счисления в другую выполним несколько примеров.
Пример 1. Представить десятичное число 581 в двоичной, восьмеричной и шестнадцатиричной системах счисления.
Задачу можно решить с минимальными затратами усилий, выполнив, например, перевод в двоичную с/с по общему правилу (т. е. делением на основание 2 по правилам десятичной системы счисления), а затем из двоичной в восьми- и шестнадцатиричную системы счисления, используя упрощенные правила (кодированием соответственно тетрад и триад).
Пример 2. Представить десятичное число 993,761 в двоичной и шестнадцатиричной системах счисления.
Задачу можно решить таким же образом, как и предыдущую.
Пример 3. Представить шестнадцатиричное число 8363 в десятичной системе счисления.
Воспользуемся общим правилом. Для этого надо исходное число делить на 10 по правилам шестнадцатиричной системы счисления.







(20) _(50) (20) 2 1 A
(30) (10) 3
5 6
Искомое число в десятичной системе равно 33635.
Дата добавления: 2019-07-15 ; просмотров: 407 ; Мы поможем в написании вашей работы!
Двоично-десятичный код
Двоично-десятичный код (англ. binary-coded decimal ), BCD, 8421-BCD — форма записи целых чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.
Например, десятичное число 31110 будет записано в двоичной системе счисления в двоичном коде как 1 0011 01112, а в двоично-десятичном коде как 0011 0001 0001BCD.
Содержание
Простой способ получения данных в формате BCD из Unsigned Integer
Имеем: Число «A» в формате U16 = 542;
Преобразуем его в BCD: (можно проделать на калькуляторе ОС Windows)
Преимущества и недостатки
Преимущества
По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.
Недостатки
Поэтому, при сложении и вычитании чисел формата 8421-BCD действуют следующие правила:
Пример операции сложения двоично-десятичных чисел:
Требуется: Найти число A = D + C, где D = 3927, C = 4856
Решение: Представим числа D и C в двоично-десятичной форме:
D = 392710 = 0011 1001 0010 0111BCD
C = 485610 = 0100 1000 0101 0110BCD
Суммируем числа D и С по правилам двоичной арифметики:
‘*’ — тетрада, из которой был перенос в старшую тетраду
‘**’ — тетрада с запрещённой комбинацией битов
В тетраду, помеченную символом *, добавляем шестёрку, так как по правилам двоичной арифметики перенос унёс с собой 16, а по правилам десятичной арифметики должен был унести 10. В тетраду, помеченную символом **, добавляем шестёрку и разрешаем распространение переноса, так как комбинация битов 1101 (что соответствует десятичному числу 13) является запрещённой.
См. также
Полезное
Смотреть что такое «Двоично-десятичный код» в других словарях:
Двоично-десятичный код — Код, в котором десятичный разряд числа выражают в двоичном коде Источник … Словарь-справочник терминов нормативно-технической документации
двоично-десятичный код — ДДЕ Метод представления десятичных чисел в двоичном коде в виде групп по четыре бита с весовыми значениями, при чтении слева направо, 8, 4, 2, 1. Примечание Каждая группа представляет одну десятичную цифру, например 0010 0011 23. [ГОСТ 30721… … Справочник технического переводчика
двоично-десятичный код — dvejetainis dešimtainis kodas statusas T sritis automatika atitikmenys: angl. binary decimal code; binary coded decimal code vok. Binärkode für Dezimalziffern, m; binärverschlüsselter Dezimalcode, m rus. двоично десятичный код, m pranc. code BCD … Automatikos terminų žodynas
Расширенный двоично-десятичный код обмена информацией — стандартный восьмибитный код, разработанный корпорацией IBM для присвоения двоичных значений буквам, цифрам, знакам пунктуации и управляющим символам. По английски: Extended Binary Coded Decimal Interchange Code Синонимы английские: EBCDIC См.… … Финансовый словарь
расширенный двоично-десятичный код обмена информацией — 01.01.43 расширенный двоично десятичный код обмена информацией [ extended binary coded decimal interchange code; EBCDIC]: Типовой код, состоящий из 8 битовых кодированных знаков. Примечание В настоящее время указанный код заменяется кодом ASCII.… … Словарь-справочник терминов нормативно-технической документации
расширенный двоично-десятичный код обмена информацией — Восьмибитовый код, используемый в вычислительных машинах фирмы IBM для кодирования знаков. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики… … Справочник технического переводчика