что это значит двоичный код

Двоичный код — где и как применяется?

Сегодня я по-особому рад своей встрече с вами, дорогие мои читатели, ведь я чувствую себя учителем, который на самом первом уроке начинает знакомить класс с буквами и цифрами. А поскольку мы живем в мире цифровых технологий, то я расскажу вам, что такое двоичный код, являющийся их основой.

Начнем с терминологии и выясним, что означит двоичный. Для пояснения вернемся к привычному нам исчислению, которое называется «десятичным». То есть, мы используем 10 знаков-цифр, которые дают возможность удобно оперировать различными числами и вести соответствующую запись.

Следуя этой логике, двоичная система предусматривает использование только двух знаков. В нашем случае, это всего лишь «0» (ноль) и «1» единица. И здесь я хочу вас предупредить, что гипотетически на их месте могли бы быть и другие условные обозначения, но именно такие значения, обозначающие отсутствие (0, пусто) и наличие сигнала (1 или «палочка»), помогут нам в дальнейшем уяснить структуру двоичного кода.

Зачем нужен двоичный код?

До появления ЭВМ использовались различные автоматические системы, принцип работы которых основан на получении сигнала. Срабатывает датчик, цепь замыкается и включается определенное устройство. Нет тока в сигнальной цепи – нет и срабатывания. Именно электронные устройства позволили добиться прогресса в обработке информации, представленной наличием или отсутствием напряжения в цепи.

Дальнейшее их усложнение привело к появлению первых процессоров, которые так же выполняли свою работу, обрабатывая уже сигнал, состоящий из импульсов, чередующихся определенным образом. Мы сейчас не будем вникать в программные подробности, но для нас важно следующее: электронные устройства оказались способными различать заданную последовательность поступающих сигналов. Конечно, можно и так описать условную комбинацию: «есть сигнал»; «нет сигнала»; «есть сигнал»; «есть сигнал». Даже можно упростить запись: «есть»; «нет»; «есть»; «есть».

Но намного проще обозначить наличие сигнала единицей «1», а его отсутствие – нулем «0». Тогда мы вместо всего этого сможем использовать простой и лаконичный двоичный код: 1011.

Безусловно, процессорная техника шагнула далеко вперед и сейчас чипы способны воспринимать не просто последовательность сигналов, а целые программы, записанные определенными командами, состоящими из отдельных символов.

Но для их записи используется все тот же двоичный код, состоящий из нулей и единиц, соответствующий наличию или отсутствию сигнала. Есть он, или его нет – без разницы. Для чипа любой из этих вариантов – это единичная частичка информации, которая получила название «бит» (bit — официальная единица измерения).

Условно, символ можно закодировать последовательностью из нескольких знаков. Двумя сигналами (или их отсутствием) можно описать всего четыре варианта: 00; 01;10; 11. Такой способ кодирования называется двухбитным. Но он может быть и:

Скажу честно, единой официальной версии нет, то так сложилось, что именно комбинация из восьми знаков стала стандартной мерой хранящейся информации, именуемой «байт». Таковая могла применяться даже к одной букве, записанной 8-и битным двоичным кодом. Итак, дорогие мои друзья, запомните пожалуйста (если кто не знал):

Так принято. Хотя символ, записанный 2-х или 32-х битным значением так же номинально можно назвать байтом. Кстати, благодаря двоичному коду мы можем оценивать объемы файлов, измеряемые в байтах и скорость передачи информации и интернета (бит в секунду).

Бинарная кодировка в действии

Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:

Расшифровка значений в ней показано в таблице.

Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:

Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.

Язык, понятный современной технике

Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:

Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:

Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.

Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.

Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.

Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.

Источник

Двоичный код.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.

Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.

На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.

Перевод натурального числа десятичной системы счисления в двоичную систему.

Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:

1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.

2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.

3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.

4. В этот момент считается, что двоичный код готов.

Для примера переведем в двоичную систему число 7:

1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.

2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.

3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.

4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.

Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.

Перевод числа двоичной системы в десятичную.

Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.

Немного из истории двоичной системы счисления.

Источник

Двоичная система для чайников

Я решил сделать серию постов по информатике для чайников.

Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.

Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.

Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.

Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:

А число 3 как три палочки:

Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:

Теперь пересчитаем – получилось 8.

Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).

В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.

Десятичная система счисления

Как мы складываем в 10-СС? Например, столбиком:

Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:

12 + 99 = [разобьем на разряды]

= (2+9) + (10+90) = [сложим первые разряды]

= 11 + (10+90) = [снова разобьем на десятки и единицы]

= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]

= 1 + (10 + 10 + 90) = [сложим десятки]

= 1 + (110) = [разобьем на сотни и десятки]

Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:

Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:

564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1

Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.

При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).

7000 = 7*1000 = 7 * 10^3

А всё число 7031 можно расписать так:

7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0

Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.

Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.

Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂

Двоичная система счисления

Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!

Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:

101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0

= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)

Теперь давайте поскладываем в двоичной системе.

Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1

Ничего удивительного, в 10-СС это точно так же выглядит.

Теперь посложнее: 1 + 1 = 10

А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.

Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?

Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!

11 + 1 = [разобьем на разряды]

= (10 + 1) + 1 = [перегруппируем]

= 10 + (1 + 1) = [О! “1+1” складывать умеем!]

= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]

Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.

Ну, и для закрепления материала сложим в 2-СС:

= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)

= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)

= (10000) + (100) + (00) + (10)

= (10000) + (100) + (00 + 10)

А по-русски: 13 + 9 = 22

Дубликаты не найдены

Берем калькулятор и перемножая двойку саму на себя подбираем максимально близкое (но меньшее 85) число

Повторяем операцию для 21

Ближайшее 16, или 2 в 4 степени

Ближайшее 4, или 2^2

1, или 2 в степени 0.

Теперь собираем наше число, проставляя единицу для той степени двойки, которая у нас встретилась (т.е. 2^6 2^4 2^2 2^0) и нуль для той степени, которая не встрети лась (2^5 2^3 2^1)

2^6 2^5 2^4 2^3 2^2 2^1 2^0

спасибо, оч доступно)

Вот этот абзац объясняет принцип записи:
——

Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:

101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0

= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
——

Можете в качестве обратной связи рассказать, что именно здесь не ясно? 🙂

Большое спасибо! Очень хорошо объяснили. Всё понял.

«не хватает перевода из десятичной в двоичную»

Да, я уже осознал этот изъян и подготовил пост про перевод из десятичной в двоичную. Завтра выложу. 🙂

«и остальных операций двоичной арифметики»

Мне показалось, что для чайников это сложновато уже. Мне лично как программисту крайне редко приходится делать с двоичным кодом что-то из арифметики, кроме сложения.

= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]= 100 «

и еще «= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)

поделитесь, пожалуйста, еще постами по информатике если есть

А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри

А теперь слушайте домашнее задание: построить синхрофазотрон.

Да просто.
6 = 1х2^2 +1х 2^1 + 0х2^0 = 110
7 = 1х2^2 + 1×2^1 + 1×2^0 = 111

7 = 4 +3 +1 = 100 + 010 + 001

Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.

Я тебя разочарую, но это десять и есть.

Ну, мы числа называем в десятичной системе, поэтому в простых случаях двоичное число переводят в десятичную в уме и так читают. 🙂

Ну ты же не называешь число В в HEX «одиннадцать», хотя оно именно 11?

Ну, и «B» я прочитаю как «одиннадцать» или как «бэ» в зависимости от контекста 🙂

Ну да. Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?

«Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?»
Не очень понял вопрос. Что с чем я должен путать, по-твоему?

«Ну а в двоичной системе, по которой ты строишь счет, понятия «два» не существует.»

Я утверждаю, что у многих чисел есть названия. И так сложилось исторически, что эти названия даны в десятичной системе.

Например, если я в унарной системе запишу:
111 + 1111 = 1111111

Я буду читать «три плюс четыре равно семь», а не «сто одиннадцать плюс тысяча сто одиннадцать равно один миллион сто тысяч. «.

Ты называл число В как 11, не смотря на то, что у тебя есть в этой же системе 11, эквивалентное десятичной 17.

Сбивает с толку? Да не больше, чем её графическая запись.

если с двоичной системы такие названия к проблемам восприятия могут и не привести, то в шестнадцатеричной точно будет путаница.

Держи мое объяснение:
Когда ты считаешь до десяти, у тебя в какой-то момент кончаются названия чисел и тебе приходится комбинировать названия, чтобы считать больше 9. Например:

Ну а в двоичной системе цифры кончаются уже после 1, так и живем:

Как ты понимаешь, от того, как мы назвали количество, само количество от этого не изменилось, изменился только способ счета.

Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0

Неправильные примеры. Да и как такового знака + и * в булевой алгебре нет

На самом деле все еще проще.

нет есть способ проще, всмысле рассказать

Нейронные сети. Формулы обратного распространения

Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.

Благодарим за создание выпуска:

Переводчика – Федора Труфанова;

Редактора – Михаила Коротеева;

Диктора – Никифора Стасова;

Монтажера – Олега Жданова

Нейронные сети. Обратное распространение ошибки

Привет, Лига образования!

Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.

В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.

Благодарим за создание выпуска:

Редактора – Михаила Коротеева;

Диктора – Никифора Стасова;

Монтажера – Олега Жданова

И бонус в комментариях, английский!

Нейронные сети. Градиентный спуск: как учатся нейронные сети

Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.

Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.

Благодарим за участие в выпуске:

Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;

Корректора – Дмитрия Мирошниченко;

Дикторов – Никифора Стасова, Дарью Яговкину;

Монтажера – Олега Жданова.

Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.

Нейронные сети. Просто о сложном

Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.

Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.

И наша первая озвучка — видео о том, что же такое нейросети.

За это отличную озвучку мы благодарим Александра Колдаева.

Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.

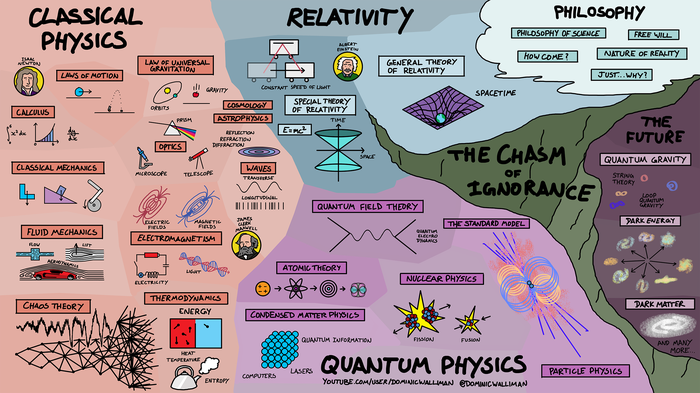
Карты наук

Выше был их автор. А вот и одна из его карт (по физике):

О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.

Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.

Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.

Вот, например, по Computer Science:

А вот по математике:

Спасибо за внимание!

За день до экзамена

Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.

Источник

Двоичное кодирование информации

Любая информация внутри компьютера хранится и обрабатывается в виде длинного кода, состоящего всего из двух символов. Этот код называется двоичным или бинарным.

По своей сути он очень похож на всем известный код Морзе, в котором двумя символами (длинный и короткий импульс) шифруются буквы для передачи текстовой информации по проводам или другим способом.

Компьютеры же пошли значительно дальше. В них в форме бинарного кода хранятся не только текстовые данные, но и программы, музыка, изображения и даже видео высокой четкости.

Перед выводом информации на экран, в аудиосистему или распечатыванием, компьютер «переводит» ее в понятный человеку язык. Но внутри компьютера она хранится и обрабатывается исключительно в виде двоичного кода.

Если вы не программист, знать систему использования бинарного кода в совершенстве не обязательно. Для понимания принципов работы компьютера достаточно разобраться с вопросом в общих чертах. В этом вам и поможет предлагаемая статья.

Содержание статьи

Почему в компьютере используется двоичный код

Люди для записи текстовой информации используют буквы. В русском языке их 33. Комбинациями из десяти цифр (от 0 до 9) мы записываем числовые данные. При работе с графической информацией пользуемся палитрой из миллионов цветов. Наши уши различают звуки в диапазоне от 16 до 20000 Гц.

Если добавить к этому обоняние, вкусовые и тактильные ощущения, получится огромнейшее разнообразие информационных импульсов, которые может воспринимать, хранить и обрабатывать наш мозг.

При помощи технических средств невозможно воссоздать аналогичную систему работы с информацией.

Людям проще всего создавать приборы, принимающие одно из двух состояний: лампочка горит или нет, магнитное поле есть или его нет и т.д. И значительно сложнее, например, заставить лампочку в разных ситуациях светиться одним из 10 цветов. Не говоря уже о 10 миллионах цветов, воспринимаемых человеком.

В технике намного удобнее иметь дело с множеством простых элементов, чем с небольшим количеством сложных.

Чтобы иметь возможность хранить и обрабатывать информацию техническими средствами, люди решили переводить ее на максимально простой «язык», состоящий всего из двух «букв» – так называемый двоичный или бинарный код.

Используя разные комбинации большого количества двух символов, в бинарном коде можно зашифровать любую числовую, текстовую, звуковую или графическую информацию.

Компьютер же является ничем иным, как машиной, предназначенной для хранения и обработки информации в таком виде.

Перевод данных в двоичный код называется кодированием.

Противоположный процесс, в результате которого бинарный код превращается в привычную для людей информацию, называется декодированием.

Компьютер осуществляет кодирование «на лету» при получении данных извне: ввод текста пользователем с клавиатуры, запись видео с веб-камеры, запись звука с микрофона и т.д.

Перед выводом информации на экран, в аудиосистему или же ее распечатыванием, происходит обратный процесс (декодирование).

Как осуществляется кодирование различных типов данных, рассмотрим немного ниже. Сначала давайте разберемся, из каких же символов формируется двоичный код внутри компьютера и как он там хранится.

С технической стороны компьютерный двоичный код реализуется наличием или отсутствием определенных свойств (импульсов) у мельчайших запоминающих элементов. Эти импульсы могут быть:

• фотооптическими

Так, поверхность любого оптического диска (CD, DVD или BluRay) состоит из спирали, которую формируют мелкие отрезки. Каждый из них может быть либо темного, либо светлого цвета. Диск быстро вращается в дисководе. На его спиральной дорожке фокусируется лазер, отражение которого попадает на фотоэлемент. Темные участки спирали поглощают свет и не передают его на фотоэлемент, светлые – наоборот, отражая свет, передают импульс фотоэлементу. В результате фотоэлемент получает информацию, зашифрованную в дорожке диска в виде темных и светлых точек.

Например, внутри жесткого диска находится быстро вращающаяся пластина. Вся ее поверхность тоже представляет собой спираль, состоящую из последовательности миллионов мелких участков. Каждый из них является элементом, который может принимать одно из двух состояний: «намагниченное», «ненамагниченное». Эти элементы и формируют двоичный код, в котором кодируется какая-то информация. Считывание состояния элементов осуществляется специальной головкой, которая быстро движется по поверхности пластины;

Например, оперативная память компьютера является микросхемой, состоящей из миллионов маленьких ячеек, созданных из микроскопических транзисторов и конденсаторов. Каждая такая ячейка может либо содержать электрический заряд, либо нет. Комбинации заряженных и разряженных ячеек оперативной памяти и формируют в ней двоичный код.

В аналогичной форме информация хранится и во всех других запоминающих микросхемах (флешки, SSD-носители и др.).

Процессор компьютера обрабатывает двоичный код тоже в виде электрических импульсов.

Иногда можно встретить ошибочное мнение, что бинарный код внутри компьютера записан в виде обычных нулей и единиц. Это следствие непонимания технической стороны вопроса. Привычных для нас нулей и единиц в компьютере нет. «Символами» компьютерного двоичного кода является наличие или отсутствие у мельчайшего запоминающего элемента определенного свойства (см. выше).

Чтобы было нагляднее, в учебных материалах отсутствие у элемента такого свойства лишь условно обозначают нулем, а его наличие – единицей. Но с таким же успехом их можно бы было обозначать точкой и тире или крестиком и ноликом.

Единицы компьютерной информации

В предыдущем пункте уже говорилось о том, что бинарный код внутри компьютера хранится в виде комбинаций большого количества элементов, каждый из которых может иметь одно из двух состояний.

Такой мельчайший элемент, участвующий в формировании бинарного кода, называется битом.

Битом является, например, каждая темная или светлая точка дорожки оптического диска, каждая запоминающая ячейка оперативной памяти компьютера и т.д.

Но каждый отдельный бит сам по себе не имеет практической ценности. Для кодирования информации используются блоки из нескольких битов.

Представим, например, что в каком-то запоминающем устройстве содержится только один бит. В нем можно будет закодировать всего одно из двух состояний чего либо, например, одну из двух цифр или один из двух цветов. Понятное дело, что практическая ценность такого носителя минимальна.

Блок из 2 битов может принимать одно из 4 состояний:

В 3-хбитном блоке можно закодировать уже одно из 8 состояний:

Ну а 8-битный блок может принимать аж 256 разных состояний. Это уже достаточно существенная частичка двоичного кода, позволяющая отобразить один из значительного количества вариантов.

Например, каждому состоянию 8-битного блока можно сопоставить какую-то букву. Вариантов, а их 256, будет достаточно для кодирования всех русских букв, включая строчные и прописные их варианты, а также всех знаков препинания. Заменяя каждую букву соответствующим 8-мибитным блоком, из двоичного кода можно составить текст.

Этот принцип и используется для записи в компьютере текстовой информации (подробнее речь об этом пойдет ниже).

Как видите, 8-битная ячейка имеет вполне реальную практическую ценность. Поэтому ее и решили считать минимальной единицей компьютерной информации. Эта единица получила название байт.

Текстовые файлы состоят из сотен, тысяч или даже десятков тысяч букв. Соответственно, для их хранения в двоичном коде требуются сотни, тысячи или десятки тысяч байтов.

Поэтому на практике гораздо чаще приходится имеет дело не с байтами, а с более крупными единицами:

• килобайтами (1 килобайт = 1024 байт);

• мегабайтами (1 мегабайт = 1024 килобайт);

• гигабайтами (1 гигабайт = 1024 мегабайт);

• терабайтами (1 терабайт = 1024 гигабайт).

Кодирование числовой информации

Для работы с числовой информацией мы пользуемся системой счисления, содержащей десять цифр: 0 1 2 3 4 5 6 7 8 9. Эта система называется десятичной.

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до 9), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до 99, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до 999 и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Система счисления, использующая только две цифры, называется двоичной.

При подсчете в двоичной системе добавлять каждый следующий разряд приходится гораздо чаще, чем в десятичной.

Вот таблица первых десяти чисел в каждой из этих систем счисления:

Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно 1 разряда. В двоичной системе для тех же целей потребуется уже 4 разряда.

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум 4 бита (0,5 байта).

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

• небольшие целые числа без знака

Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется 1 байт (8 битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

• большие целые числа и числа со знаком

Для записи каждого такого числа на запоминающем устройстве, как правило, отводится 2-байтний блок (16 битов).

Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком «плюс», этот бит остается пустым, если со знаком «минус» – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах.

Например, алгоритм кодирования числа +2676 будет следующим:

1. Перевести число 2676 из десятичной системы счисления в двоичную. В итоге получится 101001110100;

2. Записать полученное двоичное число в первые 15 бит 16-битного блока (начиная с правого края). Последний, 16-й бит, должен остаться пустым, поскольку кодируемое число имеет знак +.

В итоге +2676 в двоичном коде на запоминающем устройстве будет выглядеть так:

Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

1. Перевести число 2676 из десятичной системы счисления в двоичную. Получим все тоже двоичное число 101001110100;

2. Записать полученное двоичное число в первые 15 бит 16-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из 15 битов;

3. Записать в 16-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

Максимальным десятичным числом, которое можно закодировать в 15 битах запоминающего устройства, является 32767. Иногда для записи чисел по этому алгоритму выделяются 4-байтные блоки. В таком случае для кодирования каждого числа будет использоваться 31 бит плюс 1 бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет 2147483647 (со знаком плюс или минус).

• дробные числа со знаком

Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет 4-байтную ячейку (32 бита):

• в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком «плюс» – бит остается пустым.

• во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);

• в следующих за ним 7 битах записывается значение порядка.

• в оставшихся 23 битах записывается так называемая мантисса числа.

Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число 6,25.

Порядок кодирования будет примерно следующим:

1. Перевести десятичное число в двоичное (десятичное 6,25 равно двоичному 110,01);

3. Определить значение и знак порядка.

Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно 3 (или 11 в двоичной форме);

Знак порядка – это направление, в котором пришлось двигать запятую: влево – «плюс», вправо – «минус». В нашем примере запятая двигалась влево, поэтому знак порядка – «плюс»;

Обратите внимание, что мантисса в двоичном коде записывается, начиная с первого после запятой знака, а сама запятая упускается.

Числа с плавающей запятой, кодируемые в 32 битах, называю числами одинарной точности.

Когда для записи числа 32-битной ячейки недостаточно, компьютер может использовать ячейку из 64 битов. Число с плавающей запятой, закодированное в такой ячейке, называется числом двойной точности.

Двоичное кодирование текстовой информации

Существует несколько общепринятых стандартов кодирования текста в двоичном коде.

Одним из наиболее «старых» (разработан еще в 1960-х гг.) является стандарт ASCII (от англ. American Standard Code for Information Interchange). Это 7-битный стандарт кодирования. То есть, используя его, компьютер записывает каждую букву или знак в одну 7-битную ячейку запоминающего устройства.

Как известно, ячейка из 7 битов может принимать 128 различных состояний. Соответственно, в стандарте ASCII каждому из этих 128 состояний соответствует какая-то буква, знак препинания или специальный символ.

Дальнейшее развитие компьютерной техники показало, что 7-битный стандарт кодирования является слишком «тесным». В 128 состояниях, принимаемых 7-битной ячейкой, невозможно закодировать буквы всех существующих в мире письменностей.

Восьмибитными кодировками, распространенными в нашей стране, являются KOI8, UTF8, Windows-1251 и некоторые другие.

Разработаны также и универсальные стандарты кодирования текста (Unicode), включающие буквы большинства существующих языков. В них для записи одного символа может использоваться до 16 битов и даже больше.

Существование большого количества кодировок текста является причиной многих проблем. Вы, наверное, уже встречались с ситуацией, когда в некоторых программах на экране вместо букв отображаются непонятные «кракозябры». Это потому, что компьютер иногда «ошибается» и неверно определяет кодировку, в которой этот текст хранится в его памяти.

В перспективе, вероятно, будет принят единый стандарт кодирования текста, полностью учитывающий разнообразие существующих письменностей, на который постепенно перейдут все компьютеры, независимо от локации и используемого программного обеспечения. Но произойдет это, судя по всему, не скоро.

Кодирование изображений в двоичный код

Чтобы сохранить в двоичном коде фотографию, ее сначала виртуально разделяю на множество мелких цветных точек, называемых пикселями (что-то на подобии мозаики).

После разбивки на точки цвет каждого пикселя кодируется в бинарный код и записывается на запоминающем устройстве.

Если говорят, что размер изображения составляет, например, 512 х 512 точек, это значит, что оно представляет собой матрицу, сформированную из 262144 пикселей (количество пикселей по вертикали, умноженное на количество пикселей по горизонтали).

Прибором, «разбивающим» изображения на пиксели, является любая современная фотокамера (в том числе веб-камера, камера телефона) или сканер.

Чем на большее количество пикселей разделено изображение, тем реалистичнее выглядит фотография в декодированном виде (на мониторе или после распечатывания).

Однако качество кодирования фотографий в бинарный код зависит не только от количества пикселей, но также и от их цветового разнообразия.

Алгоритмов записи цвета в двоичном коде существует несколько. Самым распространенным из них является RGB. Эта аббревиатура – первые буквы названий трех основных цветов: красного – англ.Red, зеленого – англ. Green, синего – англ. Blue.

Из школьных уроков рисования, Вам, наверное, известно, что смешивая эти три цвета в разных пропорциях, можно получить любой другой цвет или оттенок.

На этом и построен алгоритм RGB. Каждый пиксель записывается в двоичном коде путем указания количества красного, зеленого и синего цвета, участвующего в его формировании.

Чем больше битов выделяется для кодирования пикселя, тем больше вариантов смешивания этих трех каналов можно использовать и тем значительнее будет цветовая насыщенность изображения.

Цветовое разнообразие пикселей, из которых состоит изображение, называется глубиной цвета.

Если для кодирования каждого пикселя какого-то изображения выделяется 8 битов двоичного кода, цветовое разнообразие составит 256 цветов.

Тем не менее, часто встречается и так называемая 32-битная глубина цвета. Она не предусматривает увеличение количества оттенков. Дополнительные биты, выделяемые для кодирования каждого пикселя, предназначены для регулирования степени его прозрачности или же не используются.

Описанная выше техника формирования изображений из мелких точек является наиболее распространенной и называется растровой. Но кроме растровой графики, в компьютерах используется еще и так называемая векторная графика.

Векторные изображения создаются только при помощи компьютера (фотокамеры этого делать «не умеют») и формируются не из пикселей, а из графических примитивов (линий, многоугольников, окружностей и др.).

Зачем нужна векторная графика? В известной детской песенке поется, что для изображения «человечка» достаточно нарисовать всего две «палки» и «огуречек». А представьте, насколько трудно вручную составить человечка из большого числа точек.

Векторное изображение в двоичном коде записывается как совокупность примитивов с указанием их размеров, цвета заливки, места расположения на холсте и некоторых других свойств.

Например, чтобы записать на запоминающем устройстве векторное изображение круга, компьютеру достаточно в двоичный код закодировать тип объекта (окружность), координаты его центра на холсте, длину радиуса, толщину и цвет линии, цвет заливки.

В растровой системе пришлось бы кодировать цвет каждого пикселя. И если размер изображения большой, для его хранения понадобилось бы значительно больше места на запоминающем устройстве.

Тем не менее, векторный способ кодирования не позволяет записывать в двоичном коде реалистичные фото. Поэтому все фотокамеры работают только по принципу растровой графики. Рядовому пользователю иметь дело с векторной графикой в повседневной жизни приходится не часто.

Кодирование звуковой информации

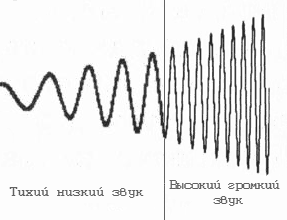
Любой звук, слышимый человеком, является колебанием воздуха, которое характеризируется двумя основными показателями: частотой и амплитудой.

Если графически изобразить звуковую волну, она будет выглядеть следующим образом:

Схему работы компьютера со звуком в общих чертах можно описать так.

Микрофон превращает колебания воздуха в аналогичные по характеристикам электрические колебания.

Динамики акустической системы или наушников имеют противоположное микрофону действие. Они превращают электрические колебания в колебания воздуха.

Но каким же образом звуковая карта преобразовывает электрические колебания в двоичный код?

Если взглянуть на графическое изображение волны и внимательно проанализировать ее геометрию, можно увидеть, что в каждый конкретный момент времени звук имеет определенную интенсивность (степень отклонения от начального состояния).

Значит если весь отрезок времени, в течение которого длится звук, разделить на очень маленькие временные участки, то звуковую волну можно будет записать как очередность значений интенсивности звука в каждом таком временном участке.

Но частота «дробления» звука должна быть достаточно высокой, иначе значения участков не будут отображать реальную геометрию волны. Вот примеры слишком низкой частоты дробления.

Описанный принцип разделения звуковой волны на мелкие участки и лежит в основе двоичного кодирования звука.

Аудиокарта компьютера разделяет звук на очень мелкие временные участки и кодирует степень интенсивности каждого из них в двоичный код. Такое «дробление» звука на части называется дискретизацией. Чем выше частота дискретизации, тем точнее фиксируется геометрия звуковой волны и тем качественней получается запись.

Так, простая речь (например, диктофонная запись) нормально воспринимается человеком, если частота дискретизации при кодировании была не ниже 8000 Гц (8 КГц). То есть, каждая секунда такой записи в двоичном коде должна состоять как минимум из 8000 частей.

Музыкальные же произведения, хранимые в компьютере, должны иметь еще более высокую частоту дискретизации. При записи стандартных звуковых CD она составляет минимум 44,1 КГц (44100 Гц).

Качество записи сильно зависит также от количества битов, используемых компьютером для кодирования каждого участка звука, полученного в результате дискретизации.

Представим, например, что для кодирования каждого такого участка компьютер использует 8 битов. Как известно, 8-битная ячейка может принимать одно из 256 значений. Но вдруг разнообразие интенсивности участков, полученных при дискретизации какого-то звука, оказалось более широким (например, 512 вариантов). В таком случае, компьютер «округлит» интенсивность участков до ближайших доступных значений чтобы «уложиться» в 256 вариантов и качество записи получится низким.

Количество битов, используемых для кодирования каждого участка звука, полученного при дискретизации, называется глубиной звука.

Глубины звука в 8-битов достаточно для кодирования простой речи. Но музыкальные произведения с такой глубиной будут звучать отвратительно. Поэтому гораздо чаще встречаются звуковые файлы, закодированные с глубиной 16, 24 или даже 32 бита.

Следует учитывать, что далеко не все устройства, предназначенные для воспроизведения «цифрового» звука, могут работать с файлами, закодированными с высокой частотой дискретизации и/или большой глубиной звука. Такие файлы могут проигрываться на одном компьютере, и «не открываться» на другом (если звуковая карта не поддерживает настолько высокий уровень дискретизации или глубины звука).

Особенности бинарного кодирования видео

Видеозапись состоит из двух компонентов: звукового и графического.

Кодирование звуковой дорожки видеофайла в двоичный код осуществляется по тем же алгоритмам, что и кодирование обычных звуковых данных (см. предыдущий пункт).

Принципы кодирования видеоизображения схожи с кодированием растровой графики (рассмотрено выше), хотя и имеют некоторые особенности.

Учитывая эту особенность, алгоритмы кодирования видео, как правило, предусматривают запись лишь первого (базового) кадра. Каждый же последующий кадр формируются путем записи его отличий от предыдущего.

Источник