что такое равномерный код
1.2. Преобразование сообщения в сигналы
1.2.1. Кодирование сообщений
Процесс передачи информации заключается в том, что сообщения преобразуются в сигналы и по системе связи передаются получателю. Получатель, зная закон соответствия между сообщениями и сигналами, может извлечь содержащуюся в сообщении информацию. Для верного декодирования каждому сигналу должно соответствовать одно определенное сообщение.
Преобразование сообщений в сигналы осуществляется с помощью кодирования и модуляции. Кодирование представляет собой отображение дискретных сообщений последовательностью символов позиционной системы счисления.
Последовательность символов, сопоставляемая одному элементарному сообщению (букве, знаку и т.д.) называется кодовой комбинацией. Систему правил преобразования элементарных сообщений в кодовые комбинации называют кодом. Основание используемой системы счисления называют основанием кода. Как правило, первичные коды задаются в виде таблиц.
При выборе основания системы счисления учитывают простоту, удобство и экономичность реализации цифрового представления информации в системе, ее преобразований и передачи по каналам связи. Наибольшее применение в технике передачи дискретной информации нашли колы с основанием 2, которые называются двоичными или бинарными. Поэтому в дальнейшем во всех случаях, где это не будет оговорено, рассматриваются двоичные коды. Символы двоичных кодов единица (1) и нуль (0) называются единичными элементами. Количество единичных элементов, образующих кодовую комбинацию, называется длиной кодовой комбинации.
Кодирование сообщений производится специальным устройством, которое называется кодером (кодирующим устройством) источника сообщения (датчика информации). В кодере кодовые комбинации представляются в виде определенных состояний накопительных элементов (триггеров, ферритов, механических рычагов, линеек и т.д.). Для передачи сообщения состояния накопительных элементов преобразуются в последовательность элементов дискретного электрического сигнала, как правило, в импульсы тока или напряжения. Каждый символ кодовой комбинации представляется единичным элементом цифрового сигнала. Процесс преобразования элементов кодовой комбинации в последовательность элементов сигнала называется модуляцией. (Ранее применялся и термин манипуляция).
В кодирующем устройстве производится первичное кодирование и первичная модуляция. Термин «первичное» подчеркивает то обстоятельство, что в процессе передачи по каналу связи сигналы, как правило, подвергаются дополнительному кодированию и модуляции.
Коды можно разделить на две большие группы: простые и корректирующие. Корректирующие коды (называют также помехоустойчивые) применяют для повышения верности информации. Простые коды (называют также: первичные, обыкновенные, безызбыточные) используются для первичного преобразования дискретных сообщений в сигналы и получаются на выходе кодера источника сообщения.
Простые код» делят на равномерные и неравномерные.
Равномерными называются такие коды, в которых все кодовые комбинации имеет одинаковую длину, т.е. имеют одинаковое число единичных элементов.
Неравномерными называют такие коды, кодовые комбинации которых могут отличаться одна от другой числом единичных элементов.
Оценка простых кодов производится по скорости передачи, помехоустойчивости и сложности технической реализации.
1.2.2. Равномерные простые коды
Как следует из определения, простые равномерные коды состоят из комбинаций одинаковой длины. Естественно, возникает вопрос:
Хорошо это или плохо?» Для ответа на этот вопрос рассмотрим следующий пример.
Пусть имеется некоторое сообщение, состоящее из М элементов, представляющее собой некоторую последовательность m(m
Универсальное двоичное кодирование. Равномерные и неравномерные коды.
Урок 9. Информатика 7 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Универсальное двоичное кодирование. Равномерные и неравномерные коды.»
На прошлом уроке мы узнали:
· Для удобства хранения и передачи информации её часто переводят из непрерывной формы в дискретную. Такой процесс называется дискретизацией.
· В процессе дискретизации информация записывается на одном из языков.
· Алфавитом языка называются все существующие символы, которые используются для представления информации на этом языке.
· Алфавит характеризуется своей мощностью, это количество символов, которые в него входят.
· Двоичный алфавит состоит из двух символов. Запись информации с помощью такого алфавита называется двоичным кодированием.
· Двоичный код – это код информации, получившийся в результате её двоичного кодирования.
· Любой алфавит можно привести к двоичному.
· Двоичное кодирование звука.
· Двоичное кодирование изображения.
· Равномерный и неравномерный коды.
· Двоичное кодирование текстовых сообщений методом Хаффмана.
Итак, на прошлом уроке мы узнали, что любой алфавит можно представить в виде двоичного, для этого каждому символу исходного алфавита присваивается его двоичный код. Записывая подряд двоичные коды всех символов, мы можем кодировать текстовые сообщения. Ещё мы узнали, что двоичный алфавит легко реализовать технически, с помощью наличия или отсутствия электрического сигнала на некотором участке электрической цепи. Именно поэтому любая информация на компьютере представлена в виде двоичного кода. Однако мы знаем, что на компьютере может храниться любая информация, а не только текстовая или числовая. Как же её представить в виде двоичного кода? Например звук и изображение. Как мы знаем, они представляются в виде непрерывных сигналов, разберёмся как же представить эти два вида информации в дискретной форме.
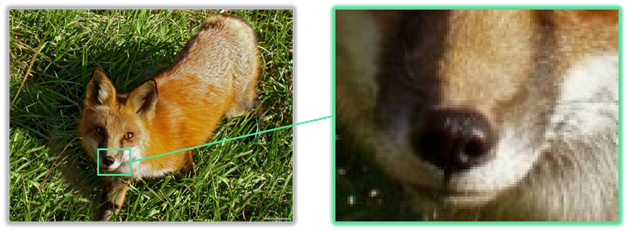
Начнём с изображения. Вполне логично, что любое изображение можно разделить на некоторые участки, каждый из которых имеет свой цвет. Именно так происходит при представлении изображений на компьютере. Изображение разбивается на маленькие фрагменты, которые можно назвать точками. Каждое изображение имеет своё разрешение. Оно состоит из двух цифр, которые разделяются крестиком или двоеточием. Число слева, означает, на сколько точек делится изображение по горизонтали, а справа – на сколько по вертикали. Таким образом изображение на компьютере представляется в виде последовательности точек, каждая из которых имеет свой цвет. То есть изображение на компьютере можно представить, последовательно записав цвета всех точек, которые в него входят.
Но как же представить цвет в виде двоичных кодов? Любой цвет на мониторе компьютера изображается смешиванием в разных количествах трёх основных цветов: красного, зелёного и синего. Такое представление цветов называется их RGB-моделью. По первым буквам названий основных цветов на английском языке, то есть «Rad», «Green» и «Blue». Так, как остальные цвета – это смеси трёх основных цветов в разных количествах, их можно представить в виде трёх чисел, количеств основных цветов. Эти числа можно заменить двоичными кодами одинаковой разрядности. Записав эти коды последовательно, мы получим двоичный код цвета точки. Таким образом изображение на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает цвет одной из точек изображения.
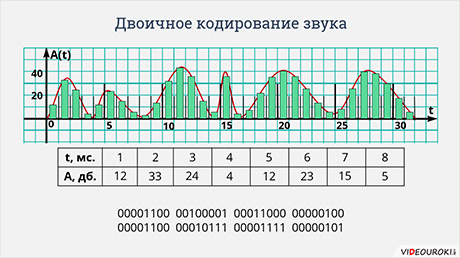
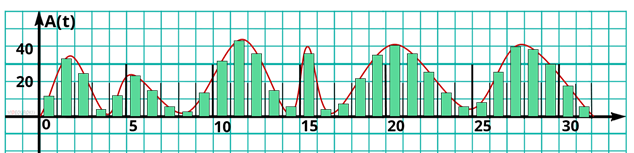
Немного иначе происходит двоичное кодирование звука. Позже из курса физики вы узнаете, что любой звук можно представить в виде непрерывной волны. Эту волну можно описать, зависимостью её амплитуды, то есть громкости звука от времени. Такую зависимость легко изобразить в виде графика. Чтобы представить звук в виде дискретных сигналов, время, в течение которого продолжается звук, делится на равные небольшие промежутки. И на каждом из промежутков заново определяется амплитуда волны, то есть громкость звука.
То, есть звук можно представить в виде списка чисел, каждое из которых означает амплитуду волны, в течение небольшого промежутка времени. Эти числа можно представить в виде двоичных кодов с одинаковым количеством разрядов. Таким образом звук на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает амплитуду звуковой волны на некотором небольшом промежутке времени.
Мы знаем, что с помощью двоичного кодирования в виде последовательности единиц и нулей можно представить любую информацию на естественном или формальном языке, в том числе изображение и звук. То есть информацию из любой формы можно представить в виде двоичного кода, что означает универсальность двоичного кодирования. Это и есть его главное преимущество. Главный недостаток двоичного кодирования – это большой размер двоичного кода. Так при кодировании текстового сообщения одному символу текста может соответствовать несколько символов двоичного кода.
Давайте подумаем, как можно уменьшить размер двоичного кода, и вообще любого кода. До этого все двоичные коды, которые мы рассматривали, были равномерными. Равномерным называется код, который состоит из равных по количеству разрядов кодовых комбинаций. Так например при кодировании алфавита для каждой буквы мы использовали двоичные коды с одинаковым количеством разрядов. Однако не все символы алфавита в текстовом сообщении, встречаются одинаково часто. Поэтому, для того, чтобы сократить длину двоичного кода мы можем присвоить разным сигналам коды разной длины. Коды с меньшей разрядностью можно присвоить сигналам, которые в сообщении встречаются чаще, а коды с большей разрядностью – сигналам, которые встречаются в сообщении реже. Такой код называется неравномерным, то есть он состоит из комбинаций различной длины.
Пример неравномерного кода – азбука Морзе. В ней разным буквам алфавита, соответствует разное количество сигналов, длинных и коротких. Например буква «А» обозначается всего двумя сигналами: одним коротким и одним длинным. А твёрдый знак кодируется пятью сигналами: двумя длинными, одним коротким и двумя длинными.
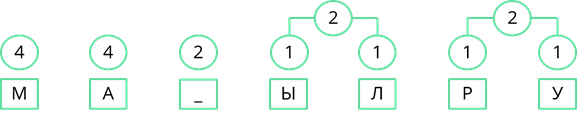
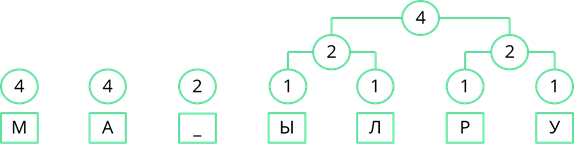
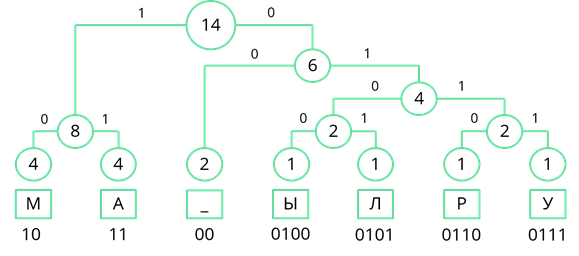
Рассмотрим один из методов неравномерного кодирования текстовых сообщений. Он называется методом Хаффмана. Посмотрим, как работает этот метод, закодировав с его помощью сообщение: «МАМА МЫЛА РАМУ». Сначала выпишем все символы алфавита, который используется в сообщении. В данном сообщении используются символы: «М», «А», пробел, «Ы», «Л», «Р» и «У». Затем нужно записать, как часто в сообщении встречается каждый из символов. Буквы «М» и «А» повторяются по четыре раза. Пробел повторяется дважды. Буквы «Ы», «Л», «Р» и «У» в сообщении встречаются по одному разу. Затем символы сообщения записываются в порядке убывания частоты появления. У нас они так и записаны.
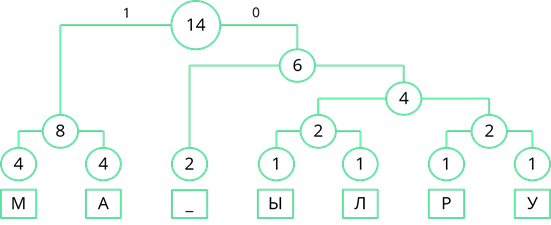
Теперь строится дерево частоты появления символов в сообщении. В начале берутся два символа, которые встречаются в сообщении реже всех. У нас таких символа четыре, возьмём два правых, буквы «Р» и «У», соединяем их линией, и складываем их частоту появления в сообщении. 1 + 1 = 2.
Теперь повторим то же действие. Реже всех у нас появлялись буквы «Ы» и «Л». Соединим их линиями сложив частоту появления получим 2.
Теперь снова смотрим где у нас самая маленькая частота появления. Таких частот у нас три. Пробел появлялся дважды, двум равны и общие частоты появления символов «Ы» и «Л», и символов «Р» и «У». Возьмём две правые частоты и объединим их. Их суммарная частота равна 4.
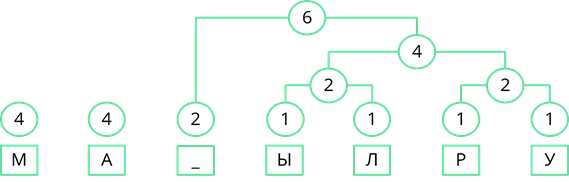
Снова ищем минимальные частоты появления. Возьмём две правые частоты и объединим их. Их сумма равна 6.
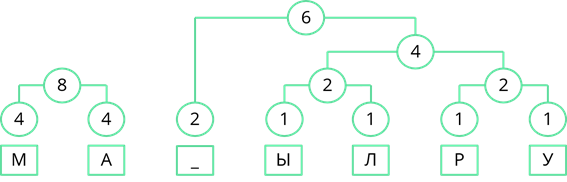
Теперь объединим две левые частоты. Их сумма равна 8.
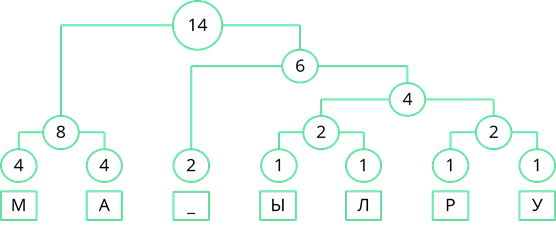
Объединим две оставшиеся частоты. Их сумма равна 14. Именно четырнадцати равна длина кодируемого сообщения.
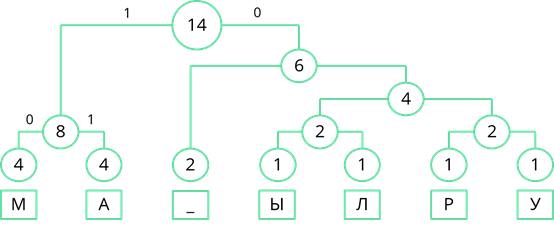
Теперь двигаясь, сверху вниз присвоим ветвям дерева значения 0 и 1. Ветви, с большей частотой будем присваивать 1, а ветви с меньшей частотой – 0. Так левой ветви верхнего узла присвоим 1, а правой – 0.
Затем рассмотрим левый узел. Там две частоты равны. Поэтому левой ветви присвоим 0, а правой – 1.
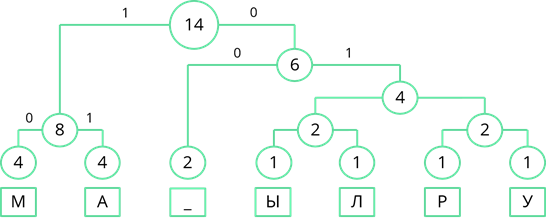
Рассмотрим узел, частота которого равна 6. Частота появления пробела меньше суммарной частоты правой ветви. Поэтому левой ветви присвоим 0, а правой ветви – 1.
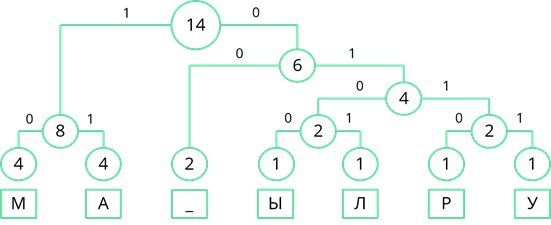
По такому же принципу пронумеруем оставшиеся ветви дерева.
Теперь, двигаясь по получившемуся дереву сверху вниз, мы можем записать двоичный код каждого символа. Так у буквы «М» будет код 10, у буквы «А» – 11, у пробела – 00 и т. д…
Теперь нам остаётся лишь заменить все символы в сообщении их двоичными кодами. В итоге двоичный код нашего сообщения будет 101110110010010001011100011011100111. Всего в нём 36 разрядов.
У некоторых из вас может возникнуть вопрос, а как же расшифровать такое сообщение, ведь в отличии от равномерного кода мы не знаем точно сколько разрядов занимает каждый символ. При неравномерном кодировании достаточно, чтобы код никакого из символов не начинался с кода другого символа. Давайте попробуем расшифровать первые символы нашего сообщения.
Итак, сообщение начинается с единицы. С единицы у нас начинаются двоичные коды букв «М» и «А», посмотрев на следующий символ 0, мы можем точно определить, что первый символ – это буква «М». По такому же принципу мы можем определить, что, следующий символ буква «А» и до конца расшифровать слово «МАМА».
Следующая цифра – 0. С нуля у нас начинаются коды пяти символов. После него идёт так же 0. С 00 у нас начинается код пробела. Далее идёт буква «М». Следующая цифра – 0. С нуля у нас начинаются коды 5 символов. Возьмём следующую цифру. С 01 начинаются коды четырёх символов. Следующая цифра – 0. С 010 начинаются коды двух символов. Следующий символ – снова 0. И мы можем однозначно определить, что это буква «Ы». Так же расшифровывается и остальное сообщение.
Давайте посмотрим, двоичный код из скольких разрядов получился бы при использовании равномерного двоичного кодирования. Как мы помним сообщение записано с помощью алфавита мощностью 7 символов. Определим, разрядность двоичного кода, необходимую для кодирования одного символа такого алфавита. Как мы помним, для этого необходимо определить, в какую степень возвести цифру 2, чтобы получить 7. Но цифру семь мы так получить не можем, поэтому результат необходимо округлить в большую сторону. Мы можем так получить 8, для этого двойку нужно возвести в 3 степень. То есть для кодирования одного символа нам потребуется 3-разрядный двоичный код. Определим, какой код потребуется для кодирования всего сообщения, для этого нужно разрядность кода одного символа, то есть 3 умножить на длину всего сообщения, то есть 14. 3 × 14 = 42. То есть при кодировании сообщения нам потребовался бы 42-разрядный равномерный двоичный код. При использовании неравномерного кода нам потребовалось всего 36 разрядов, то есть на 6 разрядов меньше.
Сокращение длины двоичного кода заметно даже при небольшой длине сообщения. Если длина сообщения будет больше, например десятки тысяч символов, разница между длинами равномерного и неравномерного кода тоже увеличится. Когда длина двоичного кода составляет миллиарды разрядов – разница между равномерным и неравномерным кодом просто огромна.
· Универсальность двоичного кодирования означает, что его можно применять для кодирования информации на любом формальном или неформальном языке, а также изображений и звука.
· Все коды можно разделить на равномерные и неравномерные, где равномерный код состоит из комбинаций равной длины, а неравномерный код состоит из комбинаций разной длины.
· Использование неравномерного кодирования позволяет сократить длину кода.
Мысли вслух
вторник, 23 октября 2012 г.
Ещё раз про однозначное декодирование
Введение
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 00, Б — 01, В — 100, Г — 101, Д — 110. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Д — 11; 2) это невозможно; 3) для буквы Г — 10; 4) для буквы Д — 10
Как показывает практика, эта задача вызывает серьезные трудности не только у многих учеников, но даже у учителей информатики.
Нужно сказать, что этот материал практически не рассматривается в существующих школьных учебниках информатики, поэтому все (как ученики, так и учителя) вынуждены разбираться самостоятельно. В то же время вузовские учебники 5, где соответствующая теория изложена строго и научно, достаточно сложны для понимания. Попробуем разобраться в сути кодирования и декодирования на школьном уровне, то есть так, как можно объяснить ученикам 8-11 классов.
В чём проблема?
Предположим, нам нужно передать сообщение по цифровым каналам связи. Для этого его необходимо закодировать, то есть сопоставить каждому символу исходного сообщения некоторый код (кодовое слово). Для определенности будем использовать двоичные коды, то есть последовательности нулей и единиц.
Пример 1. Пусть для кодирования фразы «МАМА МЫЛА ЛАМУ» выбран такой код:
| М | А | Ы | Л | У | пробел | (1) |
|---|---|---|---|---|---|---|
| 00 | 1 | 01 | 0 | 10 | 11 |
Коды букв «сцепляются» в одну битовую строку и передаются, например, по сети:
Эта цепочка битов приходит в пункт назначения, и тут возникает проблема — как восстановить исходное сообщение (конечно, при условии, что мы знаем код, то есть знаем все пары «символ–кодовое слово», которые использовались при кодировании).
Итак, мы получили 0010011100010111010010. Легко понять, что при использовании кода (1) раскодировать такое сообщение можно самыми разными способами. Например, можно предположить, что оно составлено только из букв А (код 1) и Л (код 0). Тогда получаем
В общем, ни мамы, ни ламы.
Определение. Код называется однозначно декодируемым, если любое кодовое сообщение можно расшифровать единственным способом (однозначно).
Сказанное выше означает, что код (1) НЕ является однозначно декодируемым. Как же определить, является ли заданный код однозначно декодируемым? Этим вопросом мы и займемся.
Равномерные коды
Проблема состоит в том, чтобы правильно разбить полученную битовую цепочку на отдельные кодовые слова. Для того, чтобы её решить, можно, например, использовать равномерный код, то есть код, в котором все кодовые слова имеют одинаковую длину. Например, в нашей фразе 6 символов, поэтому можно использовать 3-битный код (который позволяет закодировать 8 = 2 3 различных символов).
Пример 2. Закодируем фразу из примера 1, используя код:
| М | А | Ы | Л | У | пробел | (2) |
|---|---|---|---|---|---|---|
| 000 | 001 | 010 | 011 | 100 | 101 |
Получаем закодированное сообщение
Длина этого сообщения — 42 бита вместо 22 в предыдущем варианте, зато его легко разбить на отдельные кодовые слова и раскодировать («_» обозначает пробел):
Видим, что равномерные коды неэкономичны (закодированное сообщение в примере 2 почти в два раза длиннее, чем в примере 1), но зато декодируются однозначно.
Неравномерные коды
Для того, чтобы сократить длину сообщения, можно попробовать применить неравномерный код, то есть код, в котором кодовые слова, соответствующие разным символам исходного алфавита, могут иметь разную длину.
Пример 3. Используем для кодирования фразы из примера 1 следующий код:
| М | А | Ы | Л | У | пробел | (3) |
|---|---|---|---|---|---|---|
| 01 | 00 | 1011 | 100 | 1010 | 11 |
Получаем
Здесь 34 бита. Это, конечно, не 22, но и не 42.
Несложно показать, что эта битовая цепочка декодируется однозначно. Действительно, первая буква — М (код 01), потому что ни одно другое кодовое слово не начинается с 01. Аналогично определяем, что вторая буква — А. Действительно, за 01 следует 00 (код буквы А) и никакое другое кодовое слово не начинается с 00. Это же свойство, которое называется условием Фано, выполняется не только для кодовых слов 01 и 00, но и кодовых слов всех других букв (проверьте это самостоятельно).
Условие Фано. Никакое кодовое слово не совпадает с началом другого кодового слова.
Коды, для которых выполняется условие Фано, называют префиксными (префикс слова — это его начальный фрагмент). Все сообщения, закодированные с помощью префиксных кодов, декодируются однозначно.
Префиксные коды имеют важное практическое значение — они позволяют декодировать символы полученного сообщение по мере его получения, не дожидаясь, пока всё сообщение будет доставлено получателю.
Упражнение. Расшифруйте сообщение, закодированное кодом (3). При расшифровке кода очередной буквы не заглядывайте вперёд!
Термины «условие Фано» и «префиксный код» не используются в заданиях ЕГЭ и ГИА, однако для решения этих задача важно, чтобы ученики понимали содержание условия Фано.
Пример 4. Рассмотрим ещё один код
| М | А | Ы | Л | У | пробел | (4) |
|---|---|---|---|---|---|---|
| 10 | 00 | 1101 | 001 | 0101 | 11 |
Ясно, что он не является префиксным: код буквы А (00) совпадает с началом кода буквы Л (001) и код пробела (11) совпадает с началом кода буквы Ы (11). Закодированное сообщение
также имеет длину 34 бита, как и при использовании кода (3). Начнем раскодировать с начала. Ясно, что первой стоит буква М, потому что ни один другой код не начинается с 10. Затем — комбинация 001, которая может быть кодом буквы Л или кодом буквы А (00), за которым следует код буквы Ы или пробела. Получается, что для декодирования сообщения нам нужно «заглядывать вперёд», что очень неудобно.
Попробуем декодировать с конца битовой строки. Последние биты 0101 могут представлять только букву У, следующие 10 — только букву М и т.д. Можно проверить, что теперь сообщение однозначно декодируется с конца! Это происходит потому, что выполняется условие, которое можно назвать «обратным» условием Фано: никакое кодовое слово не совпадает с окончанием другого кодового слова. Коды, для которых выполняется обратное условие Фано, называют постфиксными (постфикс или суффикс слова — это его конечный фрагмент). В этом случае тоже обеспечивается однозначное декодирование. Таким образом,
Сообщение декодируется однозначно, если для используемого кода выполняется прямое или обратное условие Фано.
Однозначно декодируемые коды
Пример 5. Рассмотрим код, предназначенный для кодирования сообщений, состоящих только из букв А, Б и В:
| А | Б | В | (5) |
|---|---|---|---|
| 0 | 11 | 010 |
Так как код буквы А (0) совпадает как с началом, так и с концом кода буквы В (010), для этого кода не выполняются ни прямое, ни обратное условие Фано. Поэтому пока мы не можем с уверенностью сказать, декодируется ли он однозначно.
Закодируем сообщение
и попытаемся раскодировать эту строку, используя код (5). В первую очередь, замечаем, что две соседние единицы могут появиться только при использовании буквы Б (код 11), поэтому сразу выделяем две таких группы:
Здесь жёлтым фоном выделена уже декодированная часть сообщения. В оставшейся части единица может появиться только в коде буквы В (010), в битовой строке находим две такие группы:
Оставшиеся нули — это коды букв А. Анализ алгоритма показывает, что такой код всегда однозначно декодируется.
Полный ответ на вопрос об однозначной декодируемости получил в начале 1960-х годов советский математик Ал.А. Марков, предложивший решение с помощью графов [2]. Продемонстрируем его метод на примере.
Пример 6. Рассмотрим код
| А | Б | В | Г | Д | (6) |
|---|---|---|---|---|---|
| 01 | 010 | 011 | 11 | 101 |
Здесь не выполняется ни «прямое», ни «обратное» условие Фано, поэтому возможно, что декодировать сообщение однозначно не удастся. Но утверждать это заранее нельзя.
Код является однозначно декодируемым тогда и только тогда, когда в построенном таким образом графе нет ориентированных циклов, включающих вершину Λ.
Таким образом, код (6) не обладает свойством однозначной декодируемости.
Проверим таким же способом код (5), который, как мы уже выяснили, не является ни префиксным, ни постфиксным. Множество последовательностей, которые совпадают с началом и концом кодовых слов, состоит из пустой строки и единицы: <Λ, 1>. Граф, построенный с помощью приведённого выше алгоритма, содержит два узла и одну петлю:
В этом графе нет цикла, содержащего вершину Λ, поэтому любое сообщение, записанное с помощью такого кода, декодируется однозначно. Выше мы показали это с помощью простых рассуждений.
Нужно отметить, что на практике применяются, главным образом, префиксные коды, поскольку они позволяют декодировать сообщение по мере его получения, не дожидаясь окончания приёма данных.
Ещё примеры
Пример 7. Рассмотрим задачу А9 из демо-варианта КИМ ЕГЭ-2013 [1], которая сформулирована в начале статьи. Нужно оптимизировать код
выбрав один из вариантов
Решение. Сначала давайте посмотрим на исходный код, приведённый в условии. Можно заметить, что он префиксный — для него выполняется условие Фано: ни один из трехбитных кодов не начинается ни с 00 (код А), ни с 01 (код Б). Поэтому сообщения, закодированные с помощью такого кода, декодируются однозначно.
Заметим, что «обратное» условие Фано не выполняется: код буквы А (00) совпадает с окончанием кода буквы В (100), а код буквы Б (01) совпадает с окончанием кода буквы Г (101).
Теперь проверим, что получится, если сократить код буквы Д до 11 (вариант 1). Свойство однозначной декодируемости может быть потеряно только тогда, когда в результате такого сокращения нарушится условие Фано, то есть код буквы Д совпадёт с началом какого-то другого кодового слова. Видим, что этого не произошло — нет других кодовых слов, которые начинаются с 11, поэтому вариант 1 — это и есть верное решение.
Остается убедиться, что варианты 3 и 4 не подходят. Если мы сократим код буквы Г до 10 (вариант 3), условие Фано оказывается нарушенным, так как теперь код буквы Г (10) совпал с началом кода буквы В (100). Одновременно нарушено и «обратное» условие Фано: код буквы А (00) совпадает с окончанием кода буквы В (100). Но, как мы знаем, при этом код может всё-таки быть однозначно декодируемым.
Конечно, можно построить граф, как было сделано выше, и проверить, есть ли в нём циклы, включающие вершину Λ. В данном случае граф выглядит так:
Построение и анализ графа — дело достаточно трудоемкое и требующее аккуратности. Обычно в таких случаях значительно легче просто подобрать последовательность, которая может быть декодирована двумя разными способами.
Наконец, нужно убедиться, что вариант 4 не удовлетворяет условию. Если мы сократим код буквы Д до 10, условие Фано оказывается нарушенным, так как теперь код буквы Д (10) совпал с началом кода буквы В (100). Как и раньше, нарушено «обратное» условие Фано: код буквы А (00) совпадает с окончанием кода буквы В (100) и код буквы Б (01) совпадает с окончанием кода буквы Г (101).
Построим граф по методу Ал.А. Маркова:
Пример 8. Оптимизируйте код
сохранив свойство однозначной декодируемости сообщений. Выберите один из вариантов:
Решение. Определим, за счёт чего обеспечивается однозначная декодируемость исходного кода. Легко видеть, что код префиксный — для него выполняется условие Фано: ни одно из трёхбитовых кодовых слов не начинается ни с 11 (код А), ни с 10 (код Б). В то же время, обратное условие Фано не выполняется, потому что код буквы А (11) совпадает с окончанием кода буквы В (011).
Проверим вариант 1 — сократим код буквы Г до 00. При этом нарушилось условие Фано, которое обеспечивало однозначную декодируемость исходного варианта: теперь код буквы Г (00) совпадает с началом кода буквы Д (001). Но и обратное условие Фано тоже не выполняется для пары букв А-В. Поэтому можно предположить, что такой код не обладает свойством однозначной декодируемости. И действительно, легко находится цепочка 001011, которую можно раскодировать как ГБА (00 10 11) или ДВ (001 011).
Рассмотрим вариант 3 — сократим код буквы В до 01. При этом условие Фано выполняется, поскольку ни одно из кодовых слов не начинается с 01, то есть код является префиксным и однозначно раскодируется. Это и есть правильный ответ.
На всякий случай проверяем вариант 4 — сокращает код буквы Б до 1. При этом код перестает быть префиксным, и обратное условие Фано также не выполнено (код буквы Б совпадает с началом и концом кода буквы А). Сразу понятно, что последовательность 11 можно раскодировать как А или как ББ, поэтому этот вариант неверный.
Выводы
В заметке выполнен подробный анализ задачи на кодирование, которая предлагается на ЕГЭ в последние несколько лет. Нужно заметить, что в нём затрагивается вузовский курс дискретной математики. Понятно, что нельзя требовать от школьников знания теорем Ал.А. Маркова об однозначном декодировании, но учителю полезно более глубоко представлять себе эти вопросы, которые можно разбирать на факультативах. В качестве дополнительной литературы по этой теме можно рекомендовать 3.
С точки зрения практического подхода, для решения всех известных автору реальных задач подобного типа достаточно найти вариант, при котором выполняется условие Фано или обратное условие Фано (одно из двух!).
Литература
Комментарии: 16:
Спасибо, что «на пальцах» объяснили еще раз!
Действительно, спасибо. Очень понятно.
Просто великолепная статья!
Спасибо!
Уважаемый Константин! Бесконечно благодарна Вам за неоценимую помощь в подготовке детей к ЕГЭ по информатике.
Спасибо), всё понятно)))
Отличная статья! Спасибо!
Спасибо за статью. В учебнике информатики 10 класса Полякова содержится опечатка в последовательности построения графа Маркова, которая, при всей схожести текста, исправлена у вас. Порадовало также более ясное объяснение примеров.
> В учебнике информатики 10 класса Полякова содержится опечатка
Да, действительно была в первом издании. Сейчас исправлена.
Программа, скачанная отсюда, на codeTable = выдала следующий список вершин графа: [‘Lambda’, ‘0’, ‘1’].
Но разве ‘2’ не должна входит в список вершни, так как является началом ‘E’ и концом ‘C’ и не является кодовым словом?
> Но разве ‘2’ не должна входит в список вершин, так как является началом
> ‘E’ и концом ‘C’ и не является кодовым словом?
Программа предназначена только для обработки двоичных кодов.
А как можно доказать на пальцах, что из отсутствия данного граф-цикла следует однозначность декодируемости? А то зашел в учебник Маркова, а там просто жесть какая-то. Развитие моего ума не позволяет мне это изучить в разумные сроки.
Последний граф для кода А — 00, Б — 01, В — 100, Г — 101, Д — 10 составлен не совсем точно.
Нужно еще из вершины Λ в вершину 1 провести дугу Д → Г.
Подпишитесь на каналы Комментарии к сообщению [Atom]