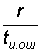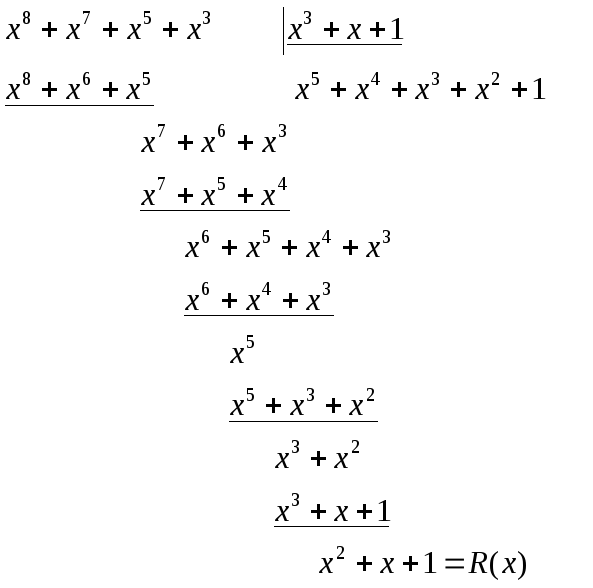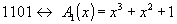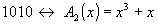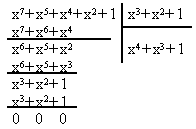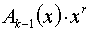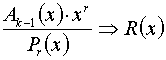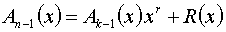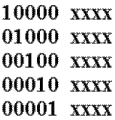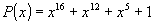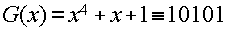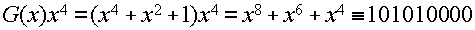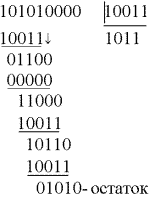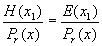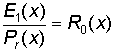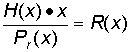что такое синдром ошибки циклического кода

17. Циклические коды. Особенности и принцип построения кодовой комбинации циклического кода. Обнаружение и исправление ошибок при циклическом кодировании. Синдром циклического кода и его свойства.

Циклический код является разновидностью помехоустойчивых кодов, применяется в технике передачи дискретных сообщений. Особенности циклических кодов заключены в двух свойствах разрешенных кодовых комбинаций:

1. любая из разрешенных кодовых комбинаций циклического кода делится по модулю два без остатка на некоторое, так называемое «образующее двоичное число», определяющее помехоустойчивые свойства кода, т.е. расстояние d;

2. циклический сдвиг разрядов разрешенной кодовой комбинации на один элемент влево порождает другую разрешенную кодовую комбинацию.

Например: 01011 и 10110 – две разрешенные кодовые комбинации некоторого циклического кода с образующим числом 1011 (d=3). Поэтому они делятся по модулю два без остатка на образующее число:

01011 1011 10110 1011

При этом d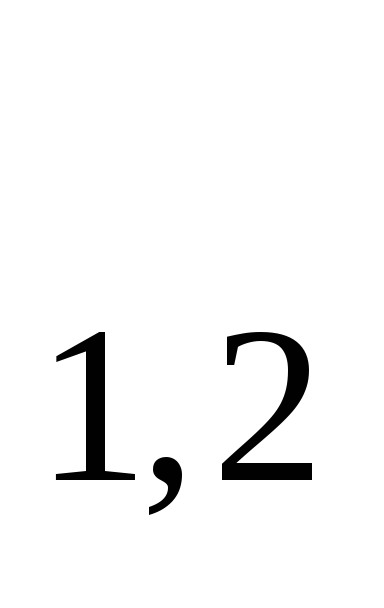=4 >d=3.

Кроме того циклический сдвиг на один разряд влево элементов первой комбинации порождают вторую комбинацию.

Делимость без остатка разрешенных кодовых комбинаций на известное образующее число лежит в основе операций обнаружения и исправления ошибок при использовании циклических кодов.

Структурная схема СПДС, содержит кодер и декодер циклического кода. Структура разрешенных кодовых комбинаций циклического кода состоит из двух частей. В начале комбинации располагается n-проверочных разрядов, структура которых определяется кодерами циклического кода из условия обеспечения делимости без остатка формируемой разрешенной кодовой комбинации на образующее число.

Идея построения циклического кода (n,k) сводится к тому, что информационную часть кодовой комбинации G(x) нужно преобразовать в комбинацию F(x), которая без остатка делится на порождающий полином Р(х) степени r=n-k. Рассмотрим последовательность операций построения циклического кода:

1. Представляем информационную часть кодовой комбинации в виде полинома G(x). Например информационная часть 110101. Тогда .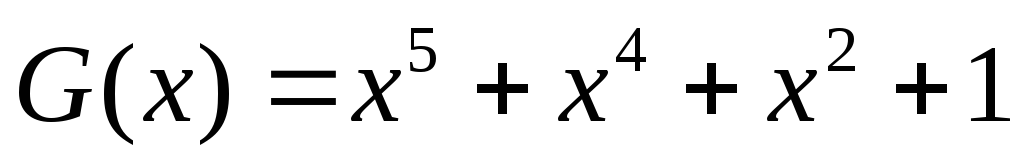

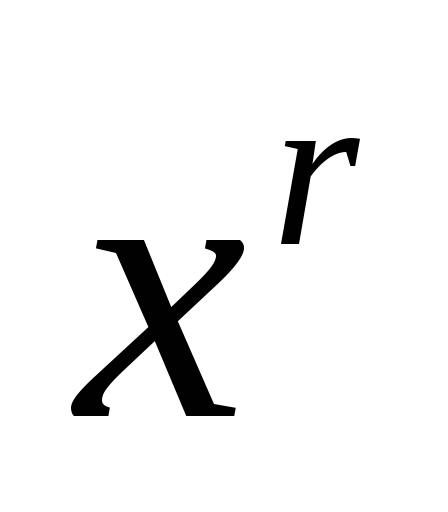
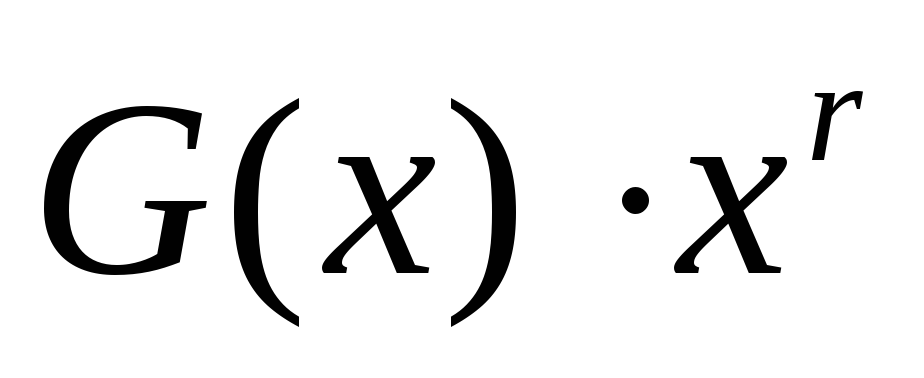
2. Умножаем G(x) на одночлен ( старшую степень порождающего полинома Р(х) ) и получаем.

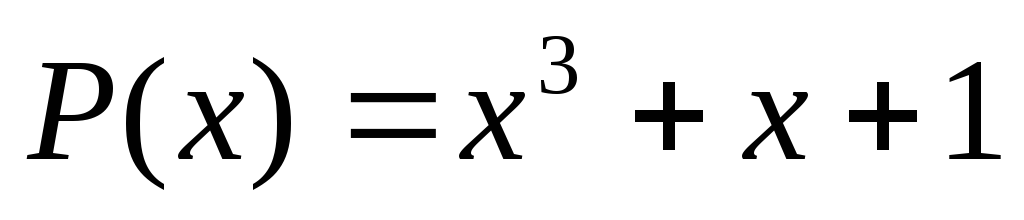
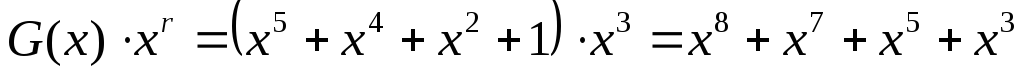
Пусть у нас порождающий полином 1011, тогда .

3. Делим 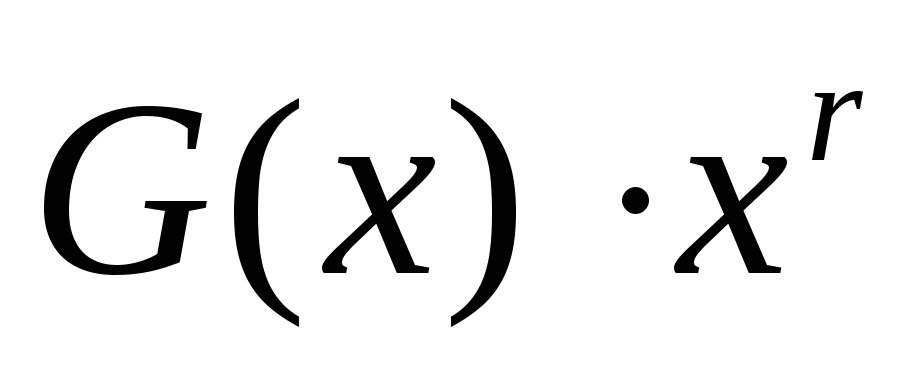на порождающий полином Р(х), при этом получаем остаток от деленияR(x).

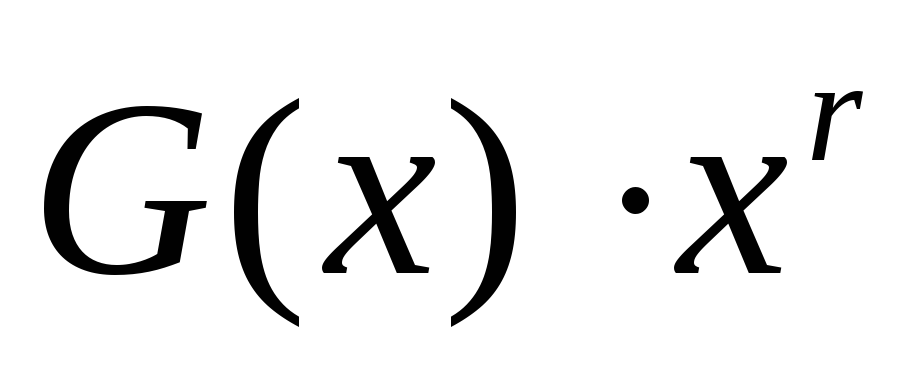
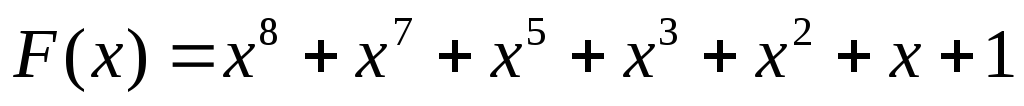
Добавим полученный остаток R (x) к комбинации и получим комбинацию, которая будет передана в линию. Данная комбинацияF(x) делится без остатка на образующий полином и представляет собой разрешенную кодовую комбинацию циклического (n,k) кода. На приеме производится деление полученной кодовой комбинации на образующий полином. Если ошибок нет, то деление пройдет без остатка. Если при делении получен остаток, то комбинация принята с ошибками.

При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.

Построение кодеров, декодеров.

Кодер строится на основе полинома P(x).

=> 1011 – веса

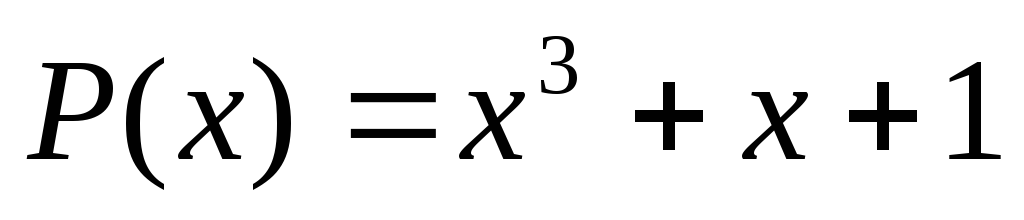
При построении устройства число ячеек регистров сдвига берется по высшей степени образующего полинома => 3 регистра сдвига; число регистров задержки берется также по высшей степени образующего полинома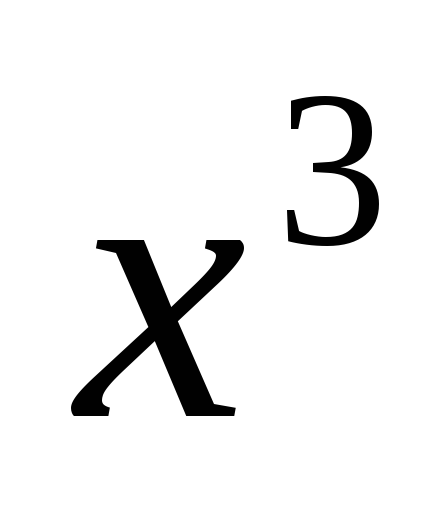; число сумматоров по модулю два берется по весовой части образующего полинома минус единица => 3-1=2m.

Источник

Что такое синдром ошибки циклического кода

Основы передачи дискретных сообщений

Тема 5. Защита от ошибок в системах связи

От СПДС обычно требуется не только передавать сообщения с заданной скоростью передачи информации, но и обеспечивать при этом требуемую достоверность.

Получив сообщение, пользователь должен быть с высокой степенью уверен, что отправлялось именно это сообщение.

Помехи, действующие в канале, как известно, приводят к возникновению ошибок. Исходная вероятность ошибки в каналах связи обычно не позволяет достичь высокой степени достоверности без применения дополнительных мероприятий. К таким мероприятиям, обеспечивающим защиту от ошибок, относят применения корректирующих кодов.

В общей структурной схеме СПДС задачу защиты от ошибок выполняет кодер и декодер канала, который иногда называют УЗО.

5.1 Понятие о корректирующих кодах

Пусть имеется источник сообщений с объемом алфавита К.

Если 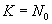, то все последовательности (или кодовые комбинации) будут использоваться для кодирования сообщений, т.е. будут разрешенными.

Полученный таким образом код называется простым, он не способен обнаруживать и исправлять ошибки.

Для того, что бы код мог обнаруживать и исправлять ошибки необходимо выполнение условия 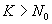, при этом неиспользуемые для передачи комбинации (N₀-K) называют запрещенными.

Появление ошибки в кодовой комбинации будет обнаружено, если передаваемая разрешенная комбинация перейдет в одну из запрещенных.

Расстояние Хемминга – характеризует степень различия кодовых комбинаций и определяется числом несовпадающих в них разрядов.

Перебрав все возможные пары разрешенных комбинаций рассматриваемого кода можно найти минимальное расстояние Хемминга d₀.

Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки.

У простого кода d₀=1 – он не обнаруживает и не исправляет ошибки. Так как любая ошибка переводит одну разрешенную комбинацию в другую.

В общем случае справедливы следующие соотношения

– для обнаруживающей способности

– для исправляющей способности

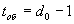
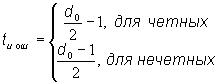
Двоичный блочный код является линейным если сумма по модулю 2 двух кодовых слов является также кодовым словом.

Линейные коды также называют групповыми.

Введем понятия группы.

Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:

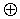
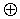
Если выполняется условие g_i g_j = g_j g_i, то группа называется коммутативной.

Множество кодовых комбинаций n-элементного кода является замкнутой группой с заданной групповой операцией сложение по модулю 2.

Поэтому используя свойство замкнутости относительно операции 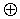2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.

Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.

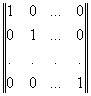
В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.

5.2 ЦИКЛИЧЕСКИЕ КОДЫ

Широкое распространение на практике получил класс линейных кодов, которые называются циклическими. Данное название происходит от основного свойства этих кодов:

если некоторая кодовая комбинация принадлежит циклическому коду, то комбинация полученная циклической перестановкой исходной комбинации (циклическим сдвигом), также принадлежит данному коду.

.

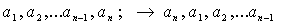
Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.

Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином.

Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.

Представление кодовой комбинации в виде многочлена.

Описание циклических кодов и их построение удобно проводить с помощью многочленов (или полиномов).

В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, n-элементную кодовую комбинацию можно описать полиномом (n-1) степени, в виде

.

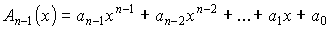
Запишем полиномы для конкретных 4-элементных комбинаций

Действия над многочленами.

При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,

,

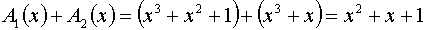
поскольку .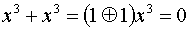

Следует отметить, что действия над коэффициентами полинома (сложение и умножение) производятся по модулю 2.

Рассмотрим операцию деления на следующем примере:

Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.

Отметим, что запись кодовой комбинации в виде многочлена, не всегда определяет длину кодовой комбинации. Например, при n = 5, многочлену 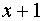соответствует кодовая комбинация 00011.

Алгоритм получения разрешенной кодовой комбинации циклического кода из комбинации простого кода

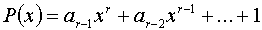
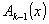
Пусть задан полином , определяющий корректирующую способность кода и число проверочных разрядов r, а также исходная комбинация простого k-элементного кода в виде многочлена .

Требуется определить разрешенную кодовую комбинацию циклического кода (n, k).

Формирование базиса (производящей матрицы) циклического кода

Формирование базиса циклического кода возможно как минимум двумя путями.

Полученная матрица и будет базисом циклического кода. Причем, в данном случае, разрешенные комбинации заведомо разделимы (т.е. информационные и проверочные элементы однозначно определены).

В данном случае код будет неразделимым.

Получив базис ЦК, можно получить все разрешенные комбинации, проводя сложение по модулю 2 кодовых комбинаций базиса в различных сочетаниях и плюс НУЛЕВАЯ.

Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом

Построение кодера циклического кода

Рассмотрим код (9,5) образованный полиномом

.

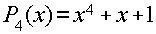
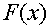
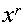
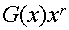
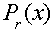
Разрешенная комбинация циклического кода образуется из комбинации простого (исходного) кода путем умножения ее на и прибавления остатка R(x) от деления на образующий полином.

Пусть

тогда

Для реализации операции добавления нулей используется r-разрядный регистр задержки.

Как видим из примера, процедура деления одного двоичного числа на другое сводится к последовательному сложению по mod2 делителя [10011] с соответствующими членами делимого [10101], затем с двоичным числом, полученным в результате первого сложения, далее с результатом второго сложения и т.д., пока число членов результирующего двоичного числа не станет меньше числа членов делителя.

Это двоичное число и будет остатком .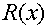

Построение формирователя остатка циклического кода

Структура устройства осуществляющего деление на полином полностью определяется видом этого полинома. Существуют правила позволяющие провести построение однозначно.

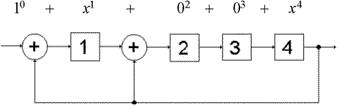
Сформулируем правила построения ФПГ.

Сумматоры ставят после каждой ячейки памяти, (начиная с нулевой) для которой существует НЕнулевой член полинома. Не ставят после ячейки для которой в полиноме нет соответствующего члена и после ячейки старшего разряда.

4. В цепь обратной связи необходимо поставить ключ, обеспечивающий правильный ввод исходных элементов и вывод результатов деления.

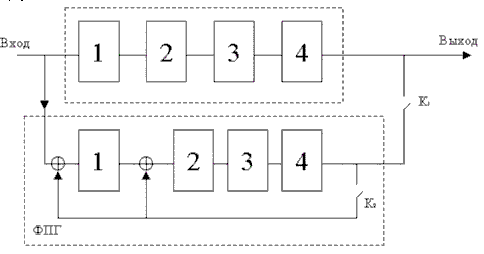
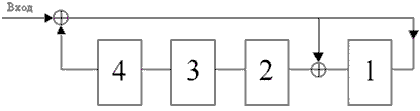
Структурная схема кодера циклического кода (9,5)

Полная структурная схема кодера приведена на следующем рисунке. Она содержит регистр задержки и рассмотренный выше формирователь проверочной группы.

Рассмотрим работу этой схемы

1. На первом этапе К₁– замкнут К₂ – разомкнут. Идет одновременное заполнение регистров задержки и сдвига информ. элементами (старший вперед!) и через 4 такта старший разряд в ячейке №4

2. Во время пятого такта К₂ – замыкается а К₁ – размыкается с этого момента в ФПГ формируется остаток. Одновременно из РЗ на выход выталкивается задержание информационные разряды.

За 5 тактов (с 5 по 9 включительно) в линию уйдут все 5-информационных элемента. К этому времени в ФПГ сформируется остаток

3. К₂ – размыкается, К₁ – замыкается и в след за информационными в линию уйдут элементы проверочной группы.

4. Одновременно идет заполнение регистров новой комбинацией.

Второй вариант построения кодера ЦК.

Рассмотренный выше кодер очень наглядно отражает процесс деления двоичных чисел. Однако можно построить кодер содержащий меньшее число элементов т.е. более экономичный.

Устройство деления на производящий полином 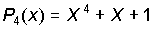можно реализовать в следующем виде:

За пять тактов в ячейках будет сформирован такой же остаток от деления, что и в рассмотренном выше Формирователе проверочной группы. (ФПГ).

За эти же 5 тактов информационные разряды, выданные сразу на модулятор.

Далее в след за информационными уходят проверочные из ячеек устройств деления.

Но важно отключить обратную связь на момент вывода проверенных элементов, иначе они исказятся.

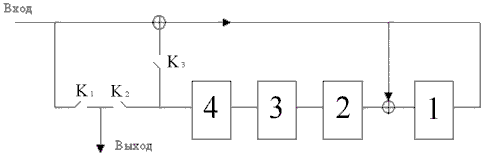
Окончательно структурная схема экономичного кодера выглядит так.

— На первом такте Кл.1 и Кл.3 замкнуты, информационные элементы проходят на выход кодера и одновременно формируются проверочные элементы.

— После того, как в линию уйдет пятый информационный элемент, в устройстве деления сформируются проверочные;

— на шестом такте ключи 1 и 3 размыкаются (разрываются обратная связь), а ключ 2 замыкается и в линию уходят проверочные разряды.

Ячейки при этом заполняются нулями и схема возвращается в исходное состояние.

Определение ошибочного разряда в ЦК.

Пусть А(х)-многочлен соответствующий переданной кодовой комбинации.

Н(х)- многочлен соответствующей принятой кодовой комбинацией.

Тогда сложение данных многочленов по модулю два даст многочлен ошибки.

E(x)=A(x) 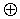H(x)

При однократной ошибке Е(х) будет содержать только один единственный член соответствующий ошибочному разряду.

Остаток – полученный от деления принятого многочлена H(x) на производящей P_r(x) равен остатку полученному при делении соответствующего многочлена ошибок E(x) на P_r(x)

При этом ошибке в каждом разряде будет соответствовать свой остаток R(x) (он же синдром), а значит, получив синдром можно однозначно определить место ошибочного разряда.

Алгоритм определения ошибки.

Пусть имеем n-элементные комбинации (n = k + r) тогда:

1. Получаем остаток от деления Е(х) соответствующего ошибке в старшем разряде [1000000000], на образующей поленом P_r(x)

2. Делим полученный полином Н(х) на P_r(x) и получаем текущий остаток R(x).

3. Сравниваем R₀(x) и R(x).

— Если они равны, то ошибка произошла в старшем разряде.

— Если «нет», то увеличиваем степень принятого полинома на Х и снова проводим деления

в) Опять сравниваем полученный остаток с R₀(x)

— Если они равны, то ошибки во втором разряде.

— Если нет, то умножаем Н(х)х 2 и повторяем эти операции до тех пор, пока R(X) не будет равен R₀(x).

Ошибка будет в разряде соответствующем числу на которое повышена степень Н(х) плюс один.

Например: 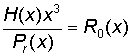то номер ошибочного разряда 3+1=4

Пример декодирования комбинации ЦК.

Положим, получена комбинация H(х)=111011010

Проанализируем её в соответствии с вышеприведенным алгоритмом.

Реализуя алгоритм определения ошибок, определим остаток от деления вектора соответствующего ошибке в старшем разряде Х 8 на производяший полином P(x)=X 4 +X+1

X 8 +X 5 +X 4 x 4 +x+1

Разделим принятую комбинацию на образующий полином

Полученный на 9-м такте остаток, как видим, не равен R₀(X). Значит необходимо умножить принятую комбинацию на Х и повторить деление. Однако результаты деления с 5 по 9 такты включительно будут такими же, значит необходимо продолжить деление после девятого такта до тех пор, пока в остатке не будет R₀(Х). В нашем случае это произойдет на 10 такте, при повышении степени на 1. Значит ошибки во втором разряде.

Декодер циклического кода с исправлением ошибки

Если ошибка в первом разряде, то остаток R₀(X)=10101 появления после девятого такта в ячейках ФПГ.

На 10 такте старший разряд покидает регистр задержки и проходит через сумматор по модулю 2.

Если и этому моменту остаток в ФПГ=R₀(X), то логическая 1 с выхода дешифратора поступит на второй вход сумматора и старший разряд инвертируется.

В нашем случае инвертируется второй разряд на 11 такте.

5.3 Выбор образующего полинома

Рассмотрим вопрос выбора образующего полинома, который определяет корректирующие свойства циклического кода. В теории циклических кодов показано, что образующий полином представляет собой произведение так называемых минимальных многочленов m_i(x), являющихся простыми сомножителями (то есть делящимся без остатка лишь на себя и на 1) бинома x n + 1:

Существуют специальные таблицы минимальных многочленов, одна из которых приведена ниже. Кроме образующего полинома необходимо найти и количество проверочных разрядов r. Оно определяется из следующего свойства циклических кодов:

для любых значений l и t_и.ош существует циклический код длины n =2 l – 1, исправляющий все ошибки кратности t_и.ош и менее, и содержащий не более 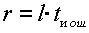проверочных элементов.

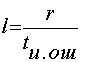
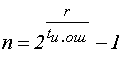
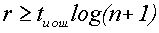
Так как , то откуда . (**)

После определения количества проверочных разрядов r, вычисления образующего полинома удобно осуществить, пользуясь таблицей минимальных многочленов, представленной в следующем виде:

Таблица минимальных многочленов

Вид минимальных многочленов для

Определяя образующий полином, нужно из столбца для соответствующего соотношения выписать все многочлены, начиная с верхней строки до нижней с номером j=2t_и.ош–1 включительно. После этого следует перемножить выбранные минимальные многочлены в соответствии с (*). В частности, если r=3, t_и.ош=1, j=2*1-1=1, образующий полином будет представлять собой единственный минимальный многочлен P(x)= m₁(x) = x 3 +x+1 (первая строка, второй столбец таблицы ). Соответственно образующее число равно 1011.

Источник