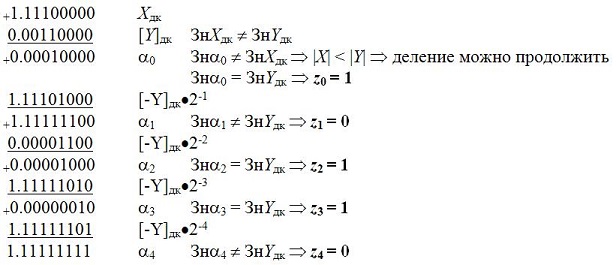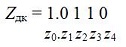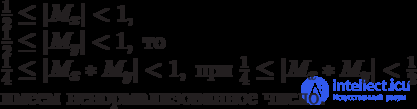деление чисел с фиксированной запятой методом без восстановления остатка в прямом коде
Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел с фиксированной запятой имеет ряд особенностей по сравнению с умножением. Главная из них заключается в том, что частное определяется по одному разряду за каждый цикл вычисления, а общее количество разрядов частного и, следовательно, циклов вычислений определяется, как правило, необходимой точностью, которая зависит как от точности исходных данных, так и от применяемых форматов чисел в конкретной ЭВМ.
В наиболее распространенных в настоящее время ЭВМ с системой команд X86 или IA-32 деление производится над числами с фиксированной точкой со знаком или без знака форматом байт или слово. При этом результат получается в виде целой части и остатка, причем каждая часть результата занимает фиксированное число байт.
Очевидно, что такой подход не может быть использован при делении чисел с фиксированной запятой, так как он предполагает, что, в общем случае, частное имеет целую часть, большую нуля, а это противоречит определению формата числа с фиксированной запятой. Для чисел, заданных в таком формате, будем исходить из следующих общих условий, не связанных со структурой конкретной ЭВМ:
Эти положения позволяют адаптировать предлагаемые алгоритмы деления к ЭВМ с произвольной архитектурой, в том числе, длине слова.
Деление чисел, заданных в прямом коде
Рассмотрим варианты деления чисел для случая, когда делимое и делитель представлены в прямом коде. При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, в общем случае, получается
При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, формируется поразрядно и так же, как и операнды, в прямом коде. Из этого следует, что в общем случае он формируется «с недостатком», так как какая-то дальнейшая цифра после прекращения выполнения операции может оказаться равной единице, тем самым увеличивая полученный результат. Это свойство может быть использовано для текущей проверки получаемых в ходе вычислений значений.
Деление со сдвигом и автоматическим восстановлением остатка
На первом этапе проводится определение знака частного:
Затем сравниваем абсолютные величины делимого и делителя.
Если α0 ≥ 0, то |X| ≥ |Y|. Следовательно, для чисел с фиксированной запятой Z = ∞, и дальнейшее деление не имеет смысла.
Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел с фиксированной запятой имеет ряд особенностей по сравнению с умножением. Главная из них заключается в том, что частное определяется по одному разряду за каждый цикл вычисления, а общее количество разрядов частного и, следовательно, циклов вычислений определяется, как правило, необходимой точностью, которая зависит как от точности исходных данных, так и от применяемых форматов чисел в конкретной ЭВМ.
В наиболее распространенных в настоящее время ЭВМ с системой команд X86 или IA-32 деление производится над числами с фиксированной точкой со знаком или без знака форматом байт или слово. При этом результат получается в виде целой части и остатка, причем каждая часть результата занимает фиксированное число байт.
Очевидно, что такой подход не может быть использован при делении чисел с фиксированной запятой, так как он предполагает, что, в общем случае, частное имеет целую часть, большую нуля, а это противоречит определению формата числа с фиксированной запятой. Для чисел, заданных в таком формате, будем исходить из следующих общих условий, не связанных со структурой конкретной ЭВМ:
Эти положения позволяют адаптировать предлагаемые алгоритмы деления к ЭВМ с произвольной архитектурой, в том числе, длине слова.
Деление чисел, заданных в прямом коде
Рассмотрим варианты деления чисел для случая, когда делимое и делитель представлены в прямом коде. При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, в общем случае, получается
При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, формируется поразрядно и так же, как и операнды, в прямом коде. Из этого следует, что в общем случае он формируется «с недостатком», так как какая-то дальнейшая цифра после прекращения выполнения операции может оказаться равной единице, тем самым увеличивая полученный результат. Это свойство может быть использовано для текущей проверки получаемых в ходе вычислений значений.
Деление со сдвигом и автоматическим восстановлением остатка
На первом этапе проводится определение знака частного:
Затем сравниваем абсолютные величины делимого и делителя.
Если α0 ≥ 0, то |X| ≥ |Y|. Следовательно, для чисел с фиксированной запятой Z = ∞, и дальнейшее деление не имеет смысла.
Выполнить деление чисел с фиксированной запятой методом без восстановления остатка (дробная часть)
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Деление без восстановления остатка
помогите у меня деление без восстановления остатка дано 1000101000/1100 Апр=0,01000101000.

Есть два множества М и N состоящие из 10 целых чисел из диапазона 1..100. Из данных множеств.
Деление без остатка
Скажите пожалуйста как разделить без остатка на языке си? Ну например 150/60=2. Только сразу скажу.

Приветствую всех. Даны целые не равные нулю числа N и K. Как вычислить минимальное целое не равное.
Ну я не уверен что все правильно излагаю, тем не менее ответ вроде сходится.
Кроме того при переписывании могли быть ошибки, поэтому надо проверять по смыслу.
«правило деления без восстановления остатков: чтобы определить цифру частного в некотором разряде, необходимо сдвинуть логически предыдущий остаток влево на один разряд, а затем алгебраически добавить к нему модуль делителя, которому приписывается знак, противоположный знаку предыдущего остатка;
если полученный остаток положителен, то в частном проставляется 1, если же остаток отрицателен, то 0″ (Лысиков, арифм и логич основы цифровых автоматов, 1980)
Далее не заморачиваясь со знаками рассмотрим деление a/b где
a=0.10011
b=0.11011
0.1011 (округляем до 4х знаков после запятой)
Проверка:
a = 0.10011 = 19/32
b = 0.11011 = 27/32
c = 19/27
Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел, заданных в дополнительном коде
Для чисел с фиксированной запятой, заданных в дополнительном коде, алгоритмы деления во многом совпадают с алгоритмами деления для чисел, заданных в прямом коде. Назовем лишь имеющиеся отличия:
Деление со сдвигом и автоматическим восстановлением остатка
Как отмечалось выше, при любом алгоритме деления получение очередного остатка связано со сложение двух чисел разных знаков. Так как при делении чисел, заданных в дополнительном коде, знак результата получается автоматически в процессе деления, то основные формулы (9.1) и (9.2) несколько изменяются по сравнению с делением чисел, заданных в прямом коде:
Если Зн α0 = Зн Xдк, то |X| ≥ |Y|. Следовательно, для чисел с фиксированной запятой Z = ∞, и дальнейшее деление не имеет смысла.
Если Зн α0 ≠ Зн Xдк, то очередные остатки при делении получаем по следующей рекуррентной формуле
 | ( 9.5) |
Очередные разряды мантиссы результата, начиная с z0, вычисляются по формуле
 | ( 9.6) |
Пример 9.5
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.0111; Yдк = 1.0110.
Решение
Результат
Пример 9.6
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.0111; Yдк = 0.0110.
Решение
Деление со сдвигом делителя и автоматическим восстановлением остатка
Данный алгоритм деления сочетает в себе черты алгоритма деления со сдвигом и автоматическим восстановлением остатка для чисел, заданных в дополнительном коде, и алгоритма деления со сдвигом делителя для чисел, заданных в прямом коде.
Первый шаг проводится по формуле
На этом шаге, определяется, превышает ли модуль делимого модуль делителя и если нет, то определяется знак частного z0, на основании следующего выражения:
 | ( 9.10) |
Очередной остаток определяется следующим образом:
 | ( 9.11) |
По соотношению знака очередного остатка и знака [Y]дк определяется очередная цифра частного согласно (9.10).
При построении арифметического устройства, использующего данный алгоритм деления, следует иметь в виду, что если мы не ориентируемся на укороченную разрядную сетку и связанные с этим механизмы коррекции результата после каждого шага вычислений, то из основных регистров необходимо иметь три 2n-разрядных регистров (для хранения делимого, делителя и остатков). Причем в число этих разрядов входит и знаковый разряд. Регистры делимого и делителя при первоначальной загрузке дополняются справа нулями. Кроме функции параллельной загрузки, регистр делителя должен иметь функцию сдвига вправо на один разряд.
Пример 9.7
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.1110; Yдк = 0.0011.
Решение
Результат
Пример 9.8
Выполнить деление двух чисел с фиксированной запятой, заданных в дополнительном коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xдк = 1.1100; Yдк = 1.1000.
Решение
На некотором шаге деления получили остаток, равный нулю. Стоит ли продолжать деление? При использовании алгоритмов деления чисел, заданных в прямом коде, деление в этом случае прекращалось, и остальные цифры результата записывались равными нулю. Но в этом случае мы получим результат
9.методы деления чисел с фиксированной запятой в прямых кодах и дополнительных (обратных) кодах.
Реализация операции деления в ЭВМ в двоичной системе счисления выполняется проще, чем в десятичной. Это объясняется тем, что при определении каждой цифры частного нужно сделать только одну пробу.
Если числа X и Y заданы в прямом коде, и они представлены с фиксированной запятой, то для выполнения деления используются два основных алгоритма:
X и Y должны быть такими, чтобы:
Арифметические операции над числами, представленными с плавающей запятой
В основе арифметических операций над числами с плавающей запятой лежат принципы, на которых базируются операции над числами сфиксированной запятой. При этом есть и некоторые особенности.
Будем условно считать, что порядки заданы в обратном коде, а мантиссы – в прямом.
Умножение:
Порядок выполнения операции следующий:
Знак произведения находится так же, как и при умножении чисел с фиксированной запятой:
Мантисса находится по правилам умножения чисел с фиксированной запятой.
При этом возможны следующие случаи:
Поэтому необходима нормализация влево максимум только на один разряд.
При умножении двух чисел в силу ограниченности разрядной сетки можно получить число, которое не может быть в ней представлено. Это соответствует получению машинной бесконечности.
В данном случае вырабатывается специальный признак, по которому дальнейшие вычисления прекращаются.
При умножении двух чисел можно получить минимальное число, которое также не может быть представлено в разрядной сетке. Это соответствует случаю, когда получаемое число должно быть интерпретировано как нуль.