для 5 букв русского алфавита заданы их двоичные коды

infoegehelp.ru

Разбор задачи A13 (демо ЕГЭ 2006)

Для 5 букв русского алфавита заданы их двоичные коды (для некоторых букв ‑ из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

В	К	А	Р	Д
000	11	01	001	10

Из четырех полученных сообщений в этой кодировке, только одно прошло без ошибки и может быть корректно декодировано. Найдите его:

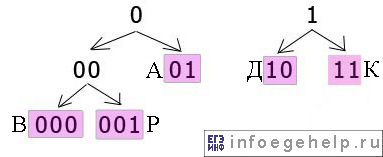
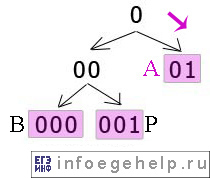
Построим графы для быстрого поиска в двоичной строке букв:

На графе розовым цветом выделены коды иcпользуемых букв.

Начнем с варианта 1:

Анализ строки 110100000100110011 происходит так:

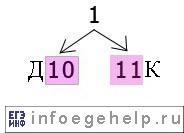
1) берем первый символ. Он равен «1», поэтому смотрим граф с вершиной, равной «1»:

Видно, что в этом графе есть коды: 10 и 11.

2) берем второй символ. Он равен «1», поэтому идем по правой ветке: 1→11. кодом «11» закодирована буква К.

После того как нашли символ, анализ снова начинаем с вершины графа.

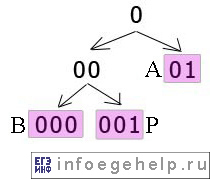
3) берем следующий третий символ. Он равен «0», поэтому смотрим граф с вершиной, равной «0»:

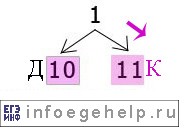
Видно, что в этом графе есть коды: 01, 000 и 001.

5)берем четвертый символ. Он равен «1», поэтому идем по правой ветке: 0→01. кодом «01» закодирована буква A.

и т.д. для остальных символов закодированной строки.

В таблицах ниже описан полный анализ всех строк:

Двоичная строка	11 01 000 001 001 10 01 1
Путь в графе до кода буквы	1→11	0→01	0→00→000	0→00→001	0→00→001	1→10	0→01	1
Двоичная строка, разбитая на коды букв	11	01	000	001	001	10	01	1
Буква	К	А	В	Р	Р	Д	А	—

Двоичная строка	11 10 10 000 01 001 001 1
Путь в графе до кода буквы	1→11	1→10	1→10	0→00→000	0→01	0→00→001	0→00→001	1
Двоичная строка, разбитая на коды букв	11	10	10	000	01	001	001	1
Буква	К	Д	Д	В	А	Р	Р	—

Двоичная строка	11 01 000 01 001 10 01 11
Путь в графе до кода буквы	1→11	0→01	0→00→000	0→01	0→00→001	1→10	0→01	1→11
Двоичная строка, разбитая на коды букв	11	01	000	01	001	10	01	11
Буква	К	А	В	А	Р	Д	А	К

Двоичная строка	11 01 10 000 10 01 10 01 0
Путь в графе до кода буквы	1→11	0→01	1→10	0→00→000	1→10	0→01	1→10	0→01	0
Двоичная строка, разбитая на коды букв	11	01	10	000	10	01	10	01	0
Буква	К	А	Д	В	Д	А	Д	А	—

Сообщения вариантов 1, 2, 4 оканчиваются кодом, которым не закодирована ни одна буква:

Сообщение варианта 3 может быть корректно декодировано.

Источник

Для 5 букв русского алфавита заданы их двоичные коды

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 1100000100110?

Мы видим, что выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова, поэтому однозначно можем раскодировать сообщение с начала.

Разобьём код слева направо по данным таблицы и переведём его в буквы:

110 000 01 001 10 — b a c d e.

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 1000110110110? Все буквы в последовательности — разные.

Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.

Будем пробовать разные варианты, отбрасывая те, в которых получаются повторяющиеся буквы:

1) 100 011 01 10 110

Первая буква определяется однозначно, её код 100: a.

Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.

Такой вариант удовлетворет условию, значит, окончательно получили ответ: acdeb.

Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

001001001111101

Какая последовательность из 6 букв закодирована двоичной строкой 011111000101100?

Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.

Будем пробовать различные варианты:

1) 011 11 100 0101100

Первая буква определяется однозначно, её код 011: D.

Вторая буква также определится однозначно — E.

Пусть третья буква B, тогда следующая начинается с кода 010, но таких букв в таблице нет, значит, предположение не верно.

2) 011 11 10 00 101 100

Третья буква — С, потом — A. Мы хотим получить ещё две буквы, чтобы в сумме их было 6, тогда следующая буква — F, и последняя — B.

Окончательно получили ответ: DECAFB.

Примечание. DECACEA не подходит, так как 7 букв.

так же подходит decacea

011 11 10 00 10 11 00

В задании спрашивается о последовательности из шести букв.

Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к каждому представлению дописывается сумма его элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110). Определите, какое число передавалось по каналу в виде 01100010100100100110.

Из примера видно, что 2 знака кодируются 10 двоичными разрядами (битами), на каждую цифру отводится 5 бит. В условии сказано, что каждая цифра записывается кодом длиной 4 знака, значит, пятую цифру можно отбросить.

Разобьём двоичную запись на группы по 5 знаков: 01100 01010 01001 00110. Отбрасываем последнюю цифру в каждой пятёрке и переводим в десятичную запись:

0110 0101 0100 0011 — 6 5 4 3.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 10; Б — 11; В — 000; Г — 001; Д — 010. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?

Для однозначного декодирования получившееся в результате сокращения кодовое слово не должно быть началом никакого другого. Второй вариант ответа не подходит, поскольку код буквы А является началом кода буквы В. Третий вариант не подходит, поскольку код буквы В является началом кода буквы Г. Четвёртый вариант ответа подходит.

Источник

infoegehelp.ru

Разбор задачи A13 (демо ЕГЭ 2005)

Определить, какой набор букв закодирован двоичной строкой 0110100011000

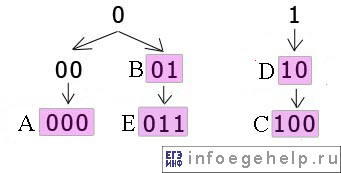
Построим графы для быстрого поиска в двоичной строке букв:

На графе розовым цветом выделены коды искомых букв.

На рисунке видно, что декодирование цепочки символов будет неоднозначным, т.к. идет дублирование (повторение) части кода другого символа. Например, в коде буквы E ( 01 1) дублируется код буквы B ( 01 ), а в коде буквы C ( 10 0) дублируется код буквы D ( 10 ).

При раскодировании последовательности будем стараться использовать буквы, код которых длиннее, чтобы быстрее рассмотреть всю последовательность. Например, если встретится последовательность 011, то сначала ее раскодируем как E. И если идущий дальше код раскодироваь нельзя, то вернемся обратно и выберем вместо E букву B. Также поступим с буквами C и D.

Анализ строки 0110100011000 происходит так:

1) берем первый символ. Он равен «0», поэтому смотрим граф с вершиной, равной «0»:

Видно, что в этом графе есть коды: 01, 000, 011.

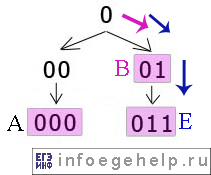
2) берем второй символ. Он равен «1», поэтому идем по правой ветке: 0→01 (на рисунке розовая стрелка). Получаем код «01». Им закодирован символ «B».

Если взять следующий 3-й символ (он равен «1»), то пойдем по ветке 0→01→011 (на рисунке синие стрелки). Получится код «011». Им закодирована буква E.

Далее анализ снова начинаем с вершины графа

3)берем четвертый символ. Он равен «0», поэтому смотрим граф с вершиной, равной «0».

Видно, что в этом графе есть коды: 01, 000, 011.

4)берем пятый символ. Он равен «1», поэтому идем по правой ветке: 0→01 (на рисунке розовая стрелка). Получаем код «01». Им закодирован символ «B».

Надо проверить, даст ли следующий (шестой) символ букву E. Он равен «0», поэтому пойдем по ветке 0→01→010. Получится код 010. Следовательно, E не получим. Остановимся на букве B.

Далее анализ снова начинаем с вершины графа

5)снова берем шестой символ. Он равен «0», поэтому смотрим граф с вершиной, равной «0».

В таблицах ниже описан анализ всей строки:

Двоичная строка	011 01 000 110 00
Путь в графе до кода буквы	0→01→011	0→01	0→00→000	1
Двоичная строка, разбитая на коды букв	011	01	000	—
Буква	E	B	A	—

Т.к. строку раскодировать не удалось, то возвращаемся к букве E. Берем вместо » E «, букву » B «:

Двоичная строка	01 10 100 011 000
Путь в графе до кода буквы	0→01	1→10	1→10→100	0→01→011	0→00→000
Двоичная строка, разбитая на коды букв	01	10	100	011	000
Буква	B	D	C	E	A

Используем метод подстановки. Для этого приведенные варианты заменим двоичными кодами:

Источник

Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.

Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.

Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.

Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.

Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.

Равномерное кодирование всегда однозначно декодируемо.

Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:

Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.

Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.

Кодирование в различных системах счисления

Для кодирования букв О, В, Д, П, А решили использовать двоичное представление

чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится

Представим коды указанных букв в дво­ич­ном коде, добавив незначащий нуль для одноразрядных чисел:

Закодируем по­сле­до­ва­тель­ность букв: ВО­ДО­ПАД — 010010001110010.

Разобьём это пред­став­ле­ние на трой­ки спра­ва на­ле­во и пе­ре­ведём каждую тройку в восьмеричное число.

010 010 001 110 010 — 22162.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из сим­во­лов А, Б, В и Г, ис­поль­зу­ет­ся по­сим­воль­ное ко­ди­ро­ва­ние: А-10, Б-11, В-110, Г-0. Через канал связи пе­ре­даётся со­об­ще­ние: ВАГ­БА­А­ГВ. За­ко­ди­руй­те со­об­ще­ние дан­ным кодом. По­лу­чен­ное дво­ич­ное число пе­ре­ве­ди­те в шест­на­дца­те­рич­ный вид.

За­ко­ди­ру­ем по­сле­до­ва­тель­ность букв: ВАГ­БА­А­ГВ — 1101001110100110. Разобьем это пред­став­ле­ние на четвёрки спра­ва на­ле­во и пе­ре­ведём каждую четверку в шестнадцатеричное число:

1101 0011 1010 0110₂ = D3A6₁₆

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Расшифровка сообщений

Для 5 букв ла­тин­ско­го ал­фа­ви­та за­да­ны их дво­ич­ные коды (для не­ко­то­рых букв – из двух бит, для не­ко­то­рых – из трех). Эти коды пред­став­ле­ны в таб­ли­це:

Опре­де­ли­те, какой набор букв за­ко­ди­ро­ван дво­ич­ной стро­кой 1000110110110, если из­вест­но, что все буквы в по­сле­до­ва­тель­но­сти – раз­ные:

Мы видим, что усло­вия Фано и об­рат­ное усло­вие Фано не вы­пол­ня­ют­ся, зна­чит код можно рас­ко­ди­ро­вать не­од­но­знач­но.

Значит, будем перебирать варианты, пока не получим подходящее слово :

1) 100 011 01 10 110

Пер­вая буква опре­де­ля­ет­ся од­но­знач­но, её код 100: a.

Пусть вто­рая буква — с, тогда сле­ду­ю­щая буква — d, потом — e и b.

Такой ва­ри­ант удо­вле­тво­ряет усло­вию, зна­чит, окон­ча­тель­но по­лу­чи­ли ответ: acdeb.

Для пе­ре­да­чи дан­ных по ка­на­лу связи ис­поль­зу­ет­ся 5-би­то­вый код. Со­об­ще­ние со­дер­жит толь­ко буквы А, Б и В, ко­то­рые ко­ди­ру­ют­ся сле­ду­ю­щи­ми ко­до­вы­ми сло­ва­ми: А — 11010, Б — 10111, В — 01101.

При пе­ре­да­че воз­мож­ны по­ме­хи. Од­на­ко не­ко­то­рые ошиб­ки можно по­пы­тать­ся ис­пра­вить. Любые два из этих трёх ко­до­вых слов от­ли­ча­ют­ся друг от друга не менее чем в трёх по­зи­ци­ях. По­это­му если при пе­ре­да­че слова про­изо­шла ошиб­ка не более чем в одной по­зи­ции, то можно сде­лать обос­но­ван­ное пред­по­ло­же­ние о том, какая буква пе­ре­да­ва­лась. (Го­во­рят, что «код ис­прав­ля­ет одну ошиб­ку».) На­при­мер, если по­лу­че­но ко­до­вое слово 10110, счи­та­ет­ся, что пе­ре­да­ва­лась буква Б. (От­ли­чие от ко­до­во­го слова для Б толь­ко в одной по­зи­ции, для осталь­ных ко­до­вых слов от­ли­чий боль­ше.) Если при­ня­тое ко­до­вое слово от­ли­ча­ет­ся от ко­до­вых слов для букв А, Б, В более чем в одной по­зи­ции, то счи­та­ет­ся, что про­изо­шла ошиб­ка (она обо­зна­ча­ет­ся ‘х’).

По­лу­че­но со­об­ще­ние 11000 11101 10001 11111. Де­ко­ди­руй­те это со­об­ще­ние — вы­бе­ри­те пра­виль­ный ва­ри­ант.

Де­ко­ди­ру­ем каж­дое слово со­об­ще­ния. Пер­вое слово: 11000 от­ли­ча­ет­ся от буквы А толь­ко одной по­зи­ци­ей. Вто­рое слово: 11101 от­ли­ча­ет­ся от буквы В толь­ко одной по­зи­ци­ей. Тре­тье слово: 10001 от­ли­ча­ет­ся от любой буквы более чем одной по­зи­ци­ей. Четвёртое слово: 11111 от­ли­ча­ет­ся от буквы Б толь­ко одной по­зи­ци­ей.

Таким об­ра­зом, ответ: АВхБ.

Однозначное кодирование

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из букв А, Б, В, Г, ре­ши­ли ис­поль­зо­вать не­рав­но­мер­ный по длине код: A=1, Б=01, В=001. Как нужно за­ко­ди­ро­вать букву Г, чтобы длина кода была ми­ни­маль­ной и до­пус­ка­лось од­но­знач­ное раз­би­е­ние ко­ди­ро­ван­но­го со­об­ще­ния на буквы?

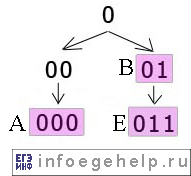
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.

Для ко­ди­ро­ва­ния не­ко­то­рой по­сле­до­ва­тель­но­сти, со­сто­я­щей из букв У, Ч, Е, Н, И и К, ис­поль­зу­ет­ся не­рав­но­мер­ный дво­ич­ный пре­фикс­ный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли со­кра­тить для одной из букв длину ко­до­во­го слова так, чтобы код по-преж­не­му остал­ся пре­фикс­ным? Коды осталь­ных букв ме­нять­ся не долж­ны.

Вы­бе­ри­те пра­виль­ный ва­ри­ант от­ве­та.

При­ме­ча­ние. Пре­фикс­ный код — это код, в ко­то­ром ни одно ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го; такие коды поз­во­ля­ют од­но­знач­но де­ко­ди­ро­вать по­лу­чен­ную дво­ич­ную по­сле­до­ва­тель­ность.

1) ко­до­вое слово для буквы Е можно со­кра­тить до 01

2) ко­до­вое слово для буквы К можно со­кра­тить до 1

3) ко­до­вое слово для буквы Н можно со­кра­тить до 10

Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

Легко заметить, что если букву Н перенести в вершину 10, она останется листом. Т.е. ко­до­вое слово для буквы Н можно со­кра­тить до 10.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ты нашел то, что искал? Поделись с друзьями!

Источник

Декодирование двоичных кодов в буквенные сообщения

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 011000101011?

Из таблицы видно, что в данной ситуации выполнено условие Фано (кодовое слово любой буквы не является началом кодового слова другой), поэтому однозначно можем раскодировать сообщение с начала.

Разбиваем двоичную строку на части (слева направо) с помощью данной в условии таблицы и переписываем ее, заменяя кодовые слова на буквы: 011|00|010|10|11 = debac.

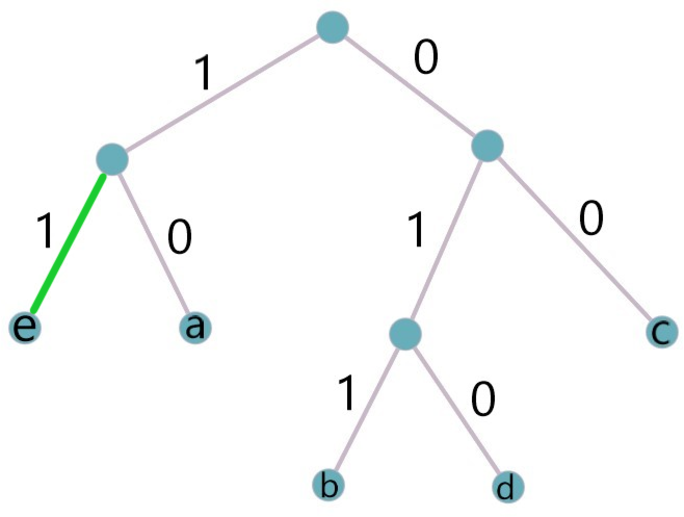
Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 101000110100100? Буквы не могут повторяться.

Из таблицы видно, что в данной ситуации не выполнены условие Фано (кодовое слово любой буквы не является началом кодового слова другой) и обратное условие Фано (кодовое слово любой буквы не является концом кодового слова другой), поэтому код нельзя раскодировать однозначно.

Разбиваем двоичную строку на части (слева направо) с помощью данной в условии таблицы (получим 2 возможных случая):

Во (2) случае мы видим повторение кодовых слов 00 и 101. Значит, случай (2) не подходит (т.к. по условию буквы не могут повторяться).

Значит, наш ответ – (1) случай. Перепишем его, заменяя кодовые слова на буквы: 101|000|11|01|00|100 = acebdf.

Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 0010001011011101?

Из таблицы видно, что в данной ситуации выполнено обратное условие Фано (кодовое слово любой буквы не является концом кодового кода другой), поэтому можем однозначно раскодировать сообщение с конца.

Разбиваем двоичную строку на части (справа налево) с помощью данной в условии таблицы и переписываем, заменяя кодовые слова на буквы: 001|00|010|110|11|101 = cdebaf.

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 100111000011? Буквы не могут повторяться.

Из таблицы видно, что в данной ситуации не выполнены условие Фано (кодовое слово любой буквы не является началом кодового слова другой) и обратное условие Фано (кодовое слово любой буквы не является концом кодового слова другой), поэтому код нельзя раскодировать однозначно.

Разбиваем двоичную строку на части (слева направо) с помощью данной в условии таблицы (получим 2 возможных случая):

Во (2) случае мы видим повторение кодовых слов 011 и 10. Значит, случай (2) не подходит (т.к. по условию буквы должны быть различные).

Значит, наш ответ – (1) случай. Перепишем его, заменяя кодовые слова на буквы: 10|01|110|00|011 = XWIZY.

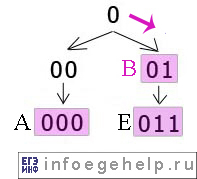
Для 4 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех), и для 1 буквы двоичный код незвестен. Эти коды представлены в таблице:

Кодовое слово буквы e такое, что оно должно быть минимально возможной длины и удовлетворять обратному условию Фано (кодовое слово любой буквы не является концом кодового слова другой).

Какой набор букв закодирован двоичной строкой 000100111110?

Чтобы выяснить двоичный код буквы e, построим граф. Так как обратное условие Фано должно выполняться, кодовое слово любой буквы не должно являться концом кодового слова другой. Значит, строим граф ”с конца” кодового слова (то есть читаем значения задом наперед: a: 01 \(\rightarrow\) 10, b: 110 \(\rightarrow\) 011, c: 00 \(\rightarrow\) 00, d: 010 \(\rightarrow\) 010).

Из графа видно, что кодовое слово минимальной длины, удовлетворяющее обратному условию Фано, – 11. Значит, кодовое слово буквы e – 11.

В данной ситуации выполнено обратное условие Фано, поэтому можем однозначно раскодировать сообщение с конца.

Разбиваем двоичную строку на части (справа налево) с помощью данной в условии таблицы и переписываем, заменяя кодовые слова на буквы: 00|010|01|11|110 = cdaeb.

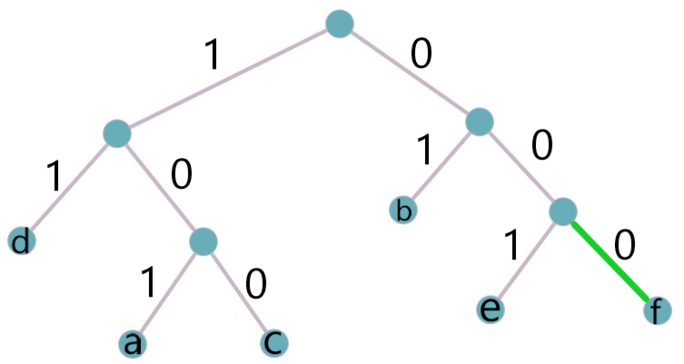
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех), и для 1 буквы двоичный код незвестен. Эти коды представлены в таблице:

Кодовое слово буквы f такое, что оно должно быть минимально возможной длины и удовлетворять условию Фано (кодовое слово любой буквы не является началом кодового кода другой).

Какой набор букв закодирован двоичной строкой 1000000010110111?

Чтобы выяснить двоичный код буквы f, построим граф. Так как условие Фано должно выполняться, кодовое слово любой буквы не должно являться началом кодового слова другой. Значит, строим граф ”с начала” кодового слова.

Из графа видно, что кодовое слово минимальной длины, удовлетворяющее условию Фано, – 000. Значит, кодовое слово буквы f – 000.

Здесь выполнено условие Фано, поэтому можем однозначно раскодировать сообщение с начала.

Разбиваем двоичную строку на части (слева направо) с помощью данной в условии таблицы и переписываем строку, заменяя кодовые слова на буквы: 100|000|001|01|101|11 = cfebad.

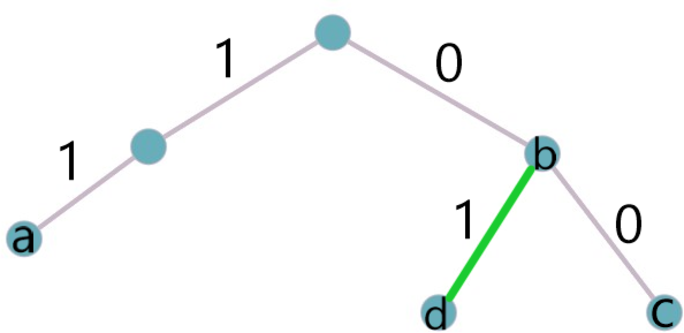
Для 3 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из одного бита, для некоторых — из двух), и для 1 буквы двоичный код незвестен. Эти коды представлены в таблице:

Кодовое буквы d такое, что оно должно быть минимально возможной длины и кодовое слово буквы b должно являться началом этого кодового слова.

Какой набор букв закодирован двоичной строкой 0100110? Буквы не могут повторяться.

Чтобы выяснить двоичный код буквы d, построим граф. Так как кодовое слово буквы b должно являться началом кодового слова d, строим граф ”с начала” кодового слова.

Из графа видно, что кодовое слово минимальной длины, началом которого является кодовое слово буквы b, – 01. Значит, кодовое слово буквы d – 01.

Из таблицы видно, что в данной ситуации не выполнены условие Фано (кодовое слово любой буквы не является началом кодового слова другой) и обратное условие Фано (кодовое слово любой буквы не является концом кодового слова другой), поэтому код нельзя раскодировать однозначно.

Разбиваем двоичную строку на части (слева направо) с помощью данной в условии таблицы (получим 2 возможных случая):

В (1) случае мы видим повторение кодового слова 01. Значит, случай (1) не подходит (по условию буквы не должны повторяться).

Значит, наш ответ – (2) случай. Перепишем его, заменяя кодовые слова на буквы: 01|00|11|0 = dcab.

Источник