если целое число 101100112 записано в дополнительном коде то десятичное значение данного числа равно
Обратный и дополнительный коды двоичных чисел
Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Вопрос № 3.1. Оригинальный порядковый номер: 8
Если числа в двоичной системе счисления имеют вид 101012 и 10002, то их разность в двоичной системе счисления равна …
Вопрос № 3.2. Оригинальный порядковый номер: 13
Результат вычисления выражения 16*8 + 4*4 + 1 в двоичной системе счисления имеет вид …
Вопрос № 3.3. Оригинальный порядковый номер: 38
Вопрос № 3.4. Оригинальный порядковый номер: 42
Среди перечисленных чисел максимальным является.
Вопрос № 3.5. Оригинальный порядковый номер: 49
Среди чисел 11111012, 1638, 7816 превышают десятичное число 11810 …
2. ни одно из чисел
Тема № 4. Кодирование данных в ЭВМ
(Задание с выбором одного правильного ответа из предложенных)
Оригинальное кол-во заданий: 17, в базе представлено: 5
Вопрос № 4.1. Оригинальный порядковый номер: 7
Вопрос № 4.2. Оригинальный порядковый номер: 9
Вопрос № 4.3. Оригинальный порядковый номер: 11
Дополнительный код числа 410 в однобайтовом формате имеет вид.
Вопрос № 4.4. Оригинальный порядковый номер: 13
Дополнительный код числа 110 в однобайтовом формате имеет вид.
Вопрос № 4.5. Оригинальный порядковый номер: 16
При байтовом кодировании алфавита максимальная мощность алфавита составляет ________ символов(а).
Тема № 5. Основные понятия алгебры логики
(Задание с выбором одного правильного ответа из предложенных)
Оригинальное кол-во заданий: 56, в базе представлено: 5
Вопрос № 5.1. Оригинальный порядковый номер: 1
Выполните подстановку операции так, чтобы равенство (1 OR 0) ________ 0 = 0 оказалось верным (здесь OR – логическое ИЛИ).
1. логическое ИЛИ (OR)
3. логическое И (AND)
4. исключающее ИЛИ (XOR)
Вопрос № 5.2. Оригинальный порядковый номер: 3
Выполните подстановку операции так, чтобы равенство (1 AND 0) ________ 1 = 0 оказалось верным (здесь AND – логическое И).
1. логическое ИЛИ (OR)
3. логическое И (AND)
4. исключающее ИЛИ (XOR)
Вопрос № 5.3. Оригинальный порядковый номер: 16
Приоритеты выполнения операций в логическом выражении в порядке убывания:
1. дизъюнкция, инверсия, конъюнкция, импликация
2. импликация, инверсия, конъюнкция, дизъюнкция
3. инверсия, конъюнкция, дизъюнкция, импликация
4. конъюнкция, инверсия, дизъюнкция, импликация
Вопрос № 5.4. Оригинальный порядковый номер: 31
1. A=1, B=0, C=1
2. A=0, B=0, C=0
3. A=0, B=0, C=1
4. A=1, B=1, C=1
Вопрос № 5.5. Оригинальный порядковый номер: 47
Для того, чтобы логическое выражение
при любых значениях логических переменных a и b всегда принимало значение “истина”, вместо знака вопроса…
1. можно поставить знак конъюнкции (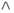 
), но не знак дизъюнкции ( 
)
2. можно поставить как знак дизъюнкции( ), так и знак конъюнкции( )
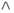
3. нельзя поставить ни знак дизъюнкции ( ), ни знак конъюнкции ( )
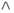
4. можно поставить знак дизъюнкции ( ), но не знак конъюнкции ( )
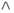
Ответ неверный
В вычислительной технике за единицу измерения информации выбрано количество информации, необходимое для различения двух равновероятных сообщений («орел-решка», «чет-нечет» и т.п.).
За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет десятичная единица информации – дит.
Ответ неверный!
Термин «бод» используют для описания скорости передачи данных.
Первоначально бод использовался в телеграфии. Число бод равно количеству значащих изменений сигнала (потенциала, фазы, частоты), происходящих в секунду.
Для двоичных сигналов нередко принимают, что бод равен биту в секунду. Однако единого мнения о правильности использования этого термина нет, особенно при высоких скоростях, где число бит в секунду не совпадает с числом бод.
Ответ неверный!
Байт – единица измерения информации, равная восьми битам. Восемь бит требуется для того, чтобы закодировать любой из 256 символов основного компьютерного кода ASCII: в соответствии с формулой Р. Хартли количество информации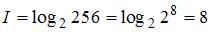 
(бит).
Задание 8. .
Для кодирования 20 различных состояний достаточно ________ двоичных разрядов.
5
Решение:
Позиции двоичного кода – это 0 или 1.
Воспользуемся формулой количества информации Р. Хартли: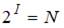 
, где в данном случае N – количество состояний, которые требуется закодировать, I – искомое число двоичных разрядов.
Имеем: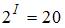 
.
Если будем использовать 4 двоичных разряда, то сможем закодировать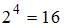 
различных состояний, чего недостаточно для выполнения условия задачи.
Если будем использовать 5 двоичных разрядов, то сможем закодировать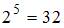 
различных состояния, то есть кодирование будет даже избыточным, с запасом ещё на 12 состояний.
Задание 9.
С помощью одного байта при двоичном кодировании можно представить целое неотрицательное число от нуля до…
Ответ: 255
Решение:
1 байт равен 8 битам, т.е. 8 двоичным разрядам. Количество различных однобайтовых двоичных кодов (00000000, 00000001, 00000010,…, 00110010,…, 11111111) равно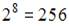 
. Следовательно, этими кодами можно представить 256 различных чисел, например, числа 0, 1, 2, 3,…, 255. Итак, максимальное число, которое можно представить однобайтовым двоичным кодом «11111111», равно 255.
Задание 10. .
Перевести двоичное число 1100101001101010111 в восьмеричную систему счисления.
ответ:
Задание 11.
Если 8-разрядный дополнительный код равен 101100112, то десятичное значение данного числа равно …
Решение:
Дополнительный код (представление числа)
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2). [2]
Содержание
Представление числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения, которое противоположно по знаку, все разряды, включая знаковый, инвертируются, а затем к результату добавляется единица.
| Десятичное представление | Код двоичного представления (8 бит) | |
|---|---|---|
| прямой | дополнительный | |
| 127 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 |
| -0 | 10000000 | ——— |
| -1 | 10000001 | 11111111 |
| -2 | 10000010 | 11111110 |
| -3 | 10000011 | 11111101 |
| -4 | 10000100 | 11111100 |
| -5 | 10000101 | 11111011 |
| -6 | 10000110 | 11111010 |
| -7 | 10000111 | 11111001 |
| -8 | 10001000 | 11111000 |
| -9 | 10001001 | 11110111 |
| -10 | 10001010 | 11110110 |
| -11 | 10001011 | 11110101 |
| -127 | 11111111 | 10000001 |
| -128 | ——— | 10000000 |
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| . | . |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| . | . |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| . | . |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| . | . |
Преобразование дополнительного кода
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1
Допишем слева знаковый единичный разряд
Для обратного преобразования используется тот же алгоритм. А именно:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1 и проверим, сложив с дополнительным кодом
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
Дополнительный код (представление числа)
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2).
Содержание
Представление отрицательного числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно 
, что равно 127.
| Десятичное представление | Код двоичного представления (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| . | . |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| . | . |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| . | . |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| . | . |
Преобразование в дополнительный код
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1
Допишем слева знаковый единичный разряд
Для обратного преобразования используется тот же алгоритм. А именно:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1 и проверим, сложив с дополнительным кодом
p-адические числа
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000. (1) равно 4444. (−1).