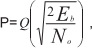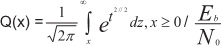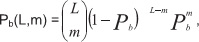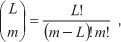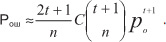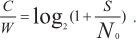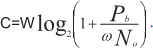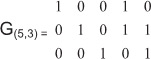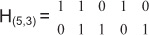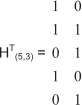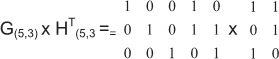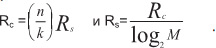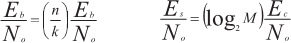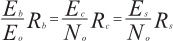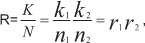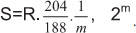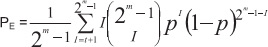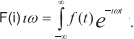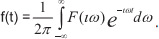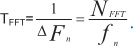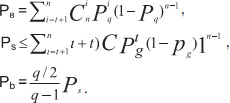избыточность кода передачи как обозначается
Московский Технический Университет Связи и Информатики
Кафедра Радиотехнических Систем
Преподаватель: Смердова Н. Е.
Студент: Матвеев А. Н.
Дата сдачи: Май 1999 года.
Известно, что каналы, по которым передается информация, практически
никогда не бывают идеальными (каналами без помех). В них почти всегда
присутствуют помехи. Отличие лишь в уровне помех и их спектральном составе.
Помехи в каналах образуются по различным причинам, но результат воздействия
их на передаваемую информацию всегда один – информация теряется
Для предотвращения потерь информации в канале были придуманы
избыточные коды (коды с избыточностью). Преимущество избыточного кода в
том, что при приеме его с искажением (количество искаженных символов
зависит от степени избыточности и структуры кода) информация может быть
восстановлена на приемнике.
Существуют избыточные коды с обнаружением (они только обнаруживают
ошибку) и коды с исправлением (эти коды обнаруживают место ошибки и
Для различных помех в канале существуют различные по своей структуре и
избыточности коды. Обычно избыточность кодов находится в пределах 10…60%
или чуть больше. Избыточность 1/4 (25%) применяется при записи информации
на лазерные диски и в системах цифрового спутникового ТВ.
Известно большое число помехоустойчивых кодов, которые
классифицируются по различным признакам. Помехоустойчивые коды можно
разделить на два больших класса: блочные и непрерывные. При блочном
кодировании последовательность элементарных сообщений источника разбивается
на отрезки и каждому отрезку ставится в соответствие определенная
последовательность (блок) кодовых символов, называемая обычно кодовой
комбинацией. Множество всех кодовых комбинаций, возможных при данном
способе блочного кодирования, и есть блочный код.
Длина блока может быть как постоянной, так и переменной. Различают
равномерные и неравномерные блочные коды. Помехоустойчивые коды являются,
как правило, равномерными.
Блочные коды бывают разделимыми и неразделимыми. К разделимым
относятся коды, в которых символы по их назначению могут быть разделены на
информационные символы, несущие информацию о сообщениях и проверочные.
Такие коды обозначаются как (n, k), где n- длина кода, k- число
информационных символов. Число комбинаций в коде не превышает 2^k. К
неразделимым относятся коды, символы которых нельзя разделить по их
назначению на информационные и проверочные.
Коды с постоянным весом характеризуются тем, что их кодовые комбинации
содержат одинаковое число единиц: Примером такого кода является код “3 из
7”, в котором каждая кодовая комбинация содержит три единицы и четыре нуля
(стандартных телеграфный код № 3).
Коды с постоянным весом позволяют обнаружить все ошибки кратности
q=1. n за исключением случаев, когда число единиц, перешедших в нули,
равно числу нулей, перешедших в единицы. В полностью асимметричных каналах,
в которых имеет место только один вид ошибок (преобразование нулей в
единицы или единиц в нули), такой код дозволяет обнаружить все ошибки. В
симметричных каналах вероятность необнаруженной ошибки можно определить как
вероятность одновременного искажения одной единицы и одного нуля:
где Pош вероятность искажения символа.
Среди разделимых кодов различают линейные и нелинейные. К линейным
относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых
слов также является кодовым словом. Линейный код называется
систематическим, если первые k символов его любой кодовой комбинации
являются информационными, остальные (n- k) символов — проверочными.
Среди линейных систематических кодов наиболее простой код (n, n-k),
содержащий один проверочный символ, который равен сумме по модулю 2 всех
информационных символов. Этот код, называемый кодом с проверкой на
четность, позволяет обнаружить все сочетания ошибок нечетной кратности.
Вероятность необнаруженной ошибки в первом приближении можно определить как
вероятность искажения двух символов:
Подклассом линейных кодов являются циклические коды. Они
характеризуются тем, что все наборы, образованные циклической перестановкой
любой кодовой комбинации, являются также кодовыми комбинациями. Это
свойство позволяет в значительной степени упростить кодирующее и
декодирующее устройства, особенно при обнаружении ошибок и исправлении
одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды
Примером нелинейного кода является код Бергера, у которого проверочные
символы представляют двоичную запись числа единиц в последовательности
информационных символов. Например, таким является код: 00000; 00101; 01001;
O111O; 10001; 10110; 11010; 11111. Коды Бергера применяются в асимметричных
каналах. В симметричных каналах они обнаруживают все одиночные ошибки и
некоторую часть многократных.
Непрерывные коды характеризуются тем, что операции кодирования и
декодирования производятся над непрерывной последовательностью символов без
разбиения ее на блоки. Среди непрерывных наиболее применимы сверточные
Как известно различают каналы с независимыми и группирующимися
ошибками. Соответственно помехоустойчивые коды можно разбить на два класса:
исправляющие независимые ошибки и исправляющие пакеты ошибок. Далее будут
рассматриваться в основном коды, исправляющие независимые ошибки. Это
объясняется тем, что хотя для исправления пакетов ошибок разработано много
эффективных кодов, на практике целесообразнее использовать коды,
исправляющие независимые ошибки вместе с устройством перемежения символов
или декорреляции ошибок. При этом символы кодовой комбинации не передаются
друг за другом, перемешиваются с символами других кодовых комбинаций. Если
интервал между символами, принадлежащими одной кодовой комбинации, сделать
больше чем “память” канала, то ошибки в пределах кодовой комбинации можно
считать независимыми, что и позволяет использовать коды, исправляющие
Блочные коды. Построение кодеков.
Из определения следует, что любой линейный код (п, k) можно получить
из k линейно независимых кодовых комбинаций путем их посимвольного
суммирования по модулю 2 в различных сочетаниях. Исходные линейно
независимые кодовые комбинации называются базисными.
Представим базисные кодовые комбинации в виде матрицы размерностью nXk
В теории кодирования она называется порождающей. Тогда процесс кодирования
заключается в выполнении операции: B=AG,
где А- вектор размерностью k, соответствующий сообщению, В- вектор
размерностью п, соответствующий кодовой комбинации.
Таким образом, порождающая матрица (7.7) содержит всю необходимую для
кодирования информацию. Она должна храниться в памяти кодирующего
устройства. Для двоичного кода объем памяти равен kXn двоичных символов.
При табличном задании кода кодирующее устройство должно запоминать
Две порождающие матрицы, которые отличаются друг от друга только
порядком расположения столбцов, задают коды, которые имеют одинаковые
расстояния Хэмминга между соответствующими кодовыми комбинациями, а
следовательно, одинаковые корректирующие способности. Такие коды называются
В качестве базисных комбинаций часто выбирают кодовые комбинации,
содержащие по одной единице среди информационных символов. При этом
порождающую матрицу удается записать в канонической форме
где I- единичная kXk подматрица, P-kX(n-k)- подматрица проверочных
символов, определяющая свойства кода. Матрица задает систематический код.
Можно показать, что для любого линейного кода существует эквивалентный
Линейный (п, k) код может быть задан проверочной матрицей Н
размерности (rХп). При этом комбинация В принадлежит коду только в том
случае, если вектор В ортогонален всем строкам матрицы Н, т. е. если
выполняется равенство (7.9)
где т—символ транспонирования матрицы. Так как это равенство справедливо
для любой кодовой комбинации, то
Каноническая форма матрицы Н имеет вид (7.10)
единичная rXr подматрица. Подставляя (7.10) в (7.9), можно получать п—k
которые называются уравнениями проверки. Из (7.11) следует, что проверочные
символы кодовых комбинаций линейного кода образуются различными линейными
комбинациями информационных символов. Единицы в любой j-й строке подматрицы
Р, входящей в проверочную матрицу (7.10), указывают, какие информационные
символы участвуют в формировании j-го проверочного символа.
Очевидно, что линейный (п, k) код можно построить, используя уравнения
проверки (7.11). При этом первые k символов кодовой комбинации
соответствии с (7.11).
С помощью проверочной матрицы сравнительно легко можно построить код с
заданным кодовым расстоянием. Это построение основано на следующей теореме:
кодовое расстояние линейного (п, k) кода равно d тогда и только тогда,
когда любые d-1 столбцов проверочной матрицы этого кода линейно независимы,
но некоторые d столбцов проверочной матрицы линейно зависимы.
Заметим, что строки проверочной матрицы линейно независимые. Поэтому
проверочную матрицу можно использовать в качестве порождающей для
некоторого другого линейного кода (п, п-k), называемого двойственным.
Кодирующее устройство для линейного (п,k) кода (рис. на предыдущей
стр.) состоит из k-разрядного сдвигающего регистра и r=п-k блоков
сумматоров по модулю 2. Информационные символы одновременно поступают на
вход регистра и на выход кодирующего устройства через коммутатор К. С
поступлением k-го информационного символа на выходах блоков сумматоров в
соответствии с уравнениями (7.11) формируются проверочные символы, которые
затем последовательно поступают на выход кодера. Процесс декодирования
сводится к выполнению операции
, где S — вектор размерностью (п-k), называемый синдромом, В- вектор
принятой кодовой комбинации.
Если принятая комбинация В совпадает с одной из разрешенных В (это
имеет место тогда, когда либо ошибки в принятых символах отсутствуют, либо
из-за действия помех одна разрешенная кодовая комбинация переходит в
В противном случае S?O, причем вид синдрома зависит только от вектора
ошибок е. Действительно,
где В- вектор, соответствующий передаваемой кодовой комбинации. При S=0
ошибок. По конкретному виду синдрома можно в пределах корректирующей
способности кода указать на ошибочные символы и их исправить.
Декодер линейного кода (рис. на следующей стр.) состоит из k-
разрядного сдвигающего регистра, (п-k) блоков сумматоров по модулю 2, схемы
сравнения, анализатора ошибок и корректора. Регистр служит для запоминания
информационных символов принятой кодовой последовательности, из которых в
блоках сумматоров формируются проверочные символы. Анализатор ошибок по
конкретному виду синдрома, получаемого в результате сравнения формируемых
на приемной стороне и принятых проверочных символов, определяет места
ошибочных символов. Исправление информационных символов производится в
корректоре. Заметим, что в общем случае при декодировании линейного кода с
исправлением ошибок в памяти декодера должна храниться таблица соответствий
между синдромами и векторами ошибок. С приходом каждой кодовой комбинации
декодер должен перебрать всю таблицу. При небольших значениях (п-k) эта
операция не вызывает затруднений. Однако для высокоэффективных кодов длиной
п, равной нескольким десяткам, разность (п-k) принимает такие значения, что
перебор таблицы оказывается практически невозможным. Например, для кода
(63, 51), имеющего кодовое расстояние d=5, таблица состоит из 2^12 = 4096
Задача заключается в выборе наилучшего (с позиции того или иного
критерия) кода. Следует заметить, что до сих пор общие методы синтеза
оптимальных линейных кодов не разработаны.
Циклические коды относятся к классу линейных систематических. Поэтому
для их построения в принципе достаточно знать порождающую матрицу.
Можно указать другой способ построения циклических кодов, основанный
на представлении кодовых комбинаций многочленами b(х) вида:
производить все алгебраические действия с учетом того, что сложение здесь
осуществляется по модулю 2.
Каждый циклический код (n, k) характеризуется так называемым
порождающим многочленом. Им может быть любой многочлен р(х) степени n-k.
Циклические коды характеризуются тем, что многочлены b(x) кодовых
комбинаций делятся без остатка на р(х). Поэтому процесс кодирования
сводится к отысканию многочлена b(x) по известным многочленам a(х) а р(х),
делящегося на р(х), где a(х)- многочлен степени k-1, соответствующий
информационной последовательности символов.
Очевидно, что в качестве многочлена b(x) можно использовать
произведение a(х)р(х). Однако при этом информационные и проверочные символы
оказываются перемешанными, что затрудняет процесс декодирования. Поэтому на
практике в основном применяется следующий метод нахождения многочлена b(x).
Умножим многочлен а(х) на и полученное произведение разделим на
где m(х)- частное, а с(х)- остаток. Так как операции суммирования и
вычитания по модулю 2 совпадают, то выражение (7.12) перепишем в виде:
Из (7.13) следует, что многочлен делится на р(х) и,
следовательно, является искомым.
Многочлен имеет следующую структуру: первые n-k членов низшего
порядка равны нулю, а коэффициенты остальных совпадают с соответствующими
коэффициентами информационного многочлена а(х). Многочлен с(х) имеет
степень меньше n-k. Таким образом, в найденном многочлене b(x) коэффициенты
при х в степени n-k и выше совпадают с информационными символами, а
коэффициенты при остальных членах, определяемых многочленом с(х), совпадают
с проверочными символами. На основе приведенных схем умножения и деления
многочленов и строятся кодирующие устройства для циклических кодов.
В качестве примера приведена схема кодера и декодера для кода (см.
рис.) с порождающим многочленом:
Код имеет кодовое расстояние d=3, что позволяет ему исправлять все
Принятая кодовая комбинация одновременно поступает в буферный регистр
сдвига, служащий для запоминания кодовой комбинации и для ее циклического
сдвига, и на устройство деления на многочлен р(х) для вычисления синдрома.
В исходном состоянии ключ находится в положении 1. После семи тактов
буферный регистр оказывается загруженным, а в регистре устройства деления
будет вычислен синдром. Если вес синдрома больше единицы, то декодер
начинает производить циклические сдвиги комбинации в буферном регистре при
отсутствии новой комбинации на входе и одновременно вычислять их синдромы
s(x)ximodp(x) в устройстве деления. Если на некотором 1-м шаге вес синдрома
окажется меньше 2, то ключ переходит в положение 2, обратные связи в
регистре деления разрываются. При последующих тактах ошибки исправляются
путем подачи содержимого регистра деления на вход сумматора по модулю 2,
включенного в буферный регистр. После семи тактов работы декодера в
автономном режиме исправленная комбинация в буферном регистре возвращается
в исходное положение (информационные символы будут занимать старшие
Существуют и другие, более универсальные, алгоритмы декодирования.
К циклическим кодам относятся коды Хэмминга, которые являются
примерами немногих известных совершенных кодов. Они имеют кодовое
расстояние d=3 и исправляют все одиночные ошибки. Среди циклических кодов
широкое применение нашли коды Боуза- Чоудхури- Хоквингема (БЧХ).
Методы описания сверточных кодов.
Кодер СК содержит регистр памяти для хранения определенного числа
информационных символов и преобразователь информационной последовательности
в кодовую последовательность. Процесс кодирования производится непрерывно.
кодера. Схема простого кодера показана на рис. 1.1а.
Информационные двоичные символы u поступают на вход регистра с К
разрядами. На выходах сумматоров по модулю 2 образуются кодовые символы
a(1) и a(2). Входы сумматоров соединены с определенными разрядами регистра.
За время одного информационного символа на выходе образуются два кодовых
символа (R= 1/2). Возможно кодирование и с другими скоростями. При скорости
2/3 на вход кодера одновременно поступает k=2 информационных символа, на
выходе при этом образуется n=3 кодовых символа. Схема такого кодера
показана на рис. 1.1,6.
Рассматриваемый код называется сверточным, постольку
последовательность кодовых символов а может быть определена как свертка
информационных символов u с импульсным откликом кодера. На рис. 1.2
показано прохождение единичной последовательности u=100… через кодер.
Символы a(1) и a(2) на его выходе образуют импульсный отклик h=
00111011 00. Таким образом, если на входе кодера действует произвольная
информационная последовательность и, то последовательность на его выходе
есть сумма по модулю 2 всех импульсных откликов, обусловленных действием
смещенных во времени символов 1. Сверточный кодер, как автомат с конечным
числом состояний, может быть описан диаграммой состояний. Диаграмма
представляет собой направленный граф и описывает все возможные переходы
кодера из одного состояния в другое, а также содержит символы выходов
кодера, которые сопровождают эти переходы.
Первоначально кодер находится в состоянии 00, и поступление на его
вход информационного символа u=0 перевозят его также в состояние 00. При
этом на выходе кодера будут символы a(1)a(2)=00. На диаграмме этот переход
обозначается петлей 00, выходящей из состояния 00 и вновь возвращающейся в
это состояние. Далее, при поступлении символа u=1 кодер переходит в
состояние 10, при этом, на выходе будут символы a(1)a(2)=11. Этот переход
из состояния 00 в состояние 10 обозначается пунктирной линией. Далее
возможно поступление на вход кодера информационных символов 0 либо 1. При
этом кодер переходит в состояние 01 либо 11, а символы на выходе будут 10
либо 01 соответственно. Процесс построения диаграммы заканчивается когда
будут просмотрены все возможные переходы из одного состояния во все
Решетчатая диаграмма является разверткой диаграммы состояний во
времени. На решетке состояния показаны узлами, а переходы соединяющими их
линиями. После каждого перехода из одного состояния в другое происходит
смещение на один шаг вправо. Решетчатая диаграмма дает наглядное
представление всех разрешенных путей, по которым может продвигаться кодер
при кодировании. Каждой информационной последовательности на входе кодера
соответствует единственный путь по решетке. Построение решетки производится
на основе диаграммы состояний. Исходное состояние S(1)S(2)=0. С
поступлением очередного символа u=0 либо 1 возможны переходы в состояния 00
либо 10, обозначаемые ветвями 00 и 11. Процесс следует продолжить, причем
через три шага очередной фрагмент, решетки будет повторяться. Пунктиром
показан путь 11100001. соответствующий поступлению на вход кодера
информационной последовательности 1011.
Для описания кодера последовательности символов на его входе и выходе
представляют с использованием оператора задержки:
Здесь индексы в скобках обозначают: i- номер входа кодера, 1? j? n, j-
дискретные моменты времени.
Процесс кодирования может быть представлен как умножение многочлена
входной информационной последовательности u(D) на порождающие многочлены
кода G(j)(D), которые описывают связи ячеек регистра кодера с его выходами
Порождающий многочлен представим в виде ряда (1.2):
СК можно также задавать порождающей матрицей (1.3):
Порождающая матрица состоит из сдвигов базисной порождающей матрицы
(верхняя строка матрицы О), которая, в свею очередь, состоит из
элементарных матриц Gi, 0?i?k-1, содержащих k строк и n столбцов.
Элементами этих матриц двоичных кодов являются символы 0 и 1.
Как при использовании блоковых кодов, процесс кодирования может быть
представлен в матричной форме: A=UG (1.4)
,где U- полубесконечная матрица входных информационных символов, А-
полубесконечная матрица символов на выходе кодера.
Декодирование сверточных кодов.
Алгебраические методы декодирования основаны на использовании
алгебраических свойств кодовых последовательностей. В ряде случаев эти
методы приводят к простым реализациям кодека. Такие алгоритмы являются
неоптимальными, так как используемые алгебраические процедуры декодирования
предназначены для исправления конкретных (и не всех) конфигураций ошибок в
канале. Алгебраические методы отождествляют с поэлементным приемом
последовательностей, который для кодов с избыточностью, как известно, дает
худшие результаты, чем прием в целом.
Вероятностные методы декодирования значительно ближе к оптимальному
приему в целом, так как в этом случае декодер оперирует с величинами,
пропорциональными вероятностям, оценивает и сравнивает вероятности
различных гипотез и на этой основе выносит решения о передаваемых символах.
Вероятностные методы декодирования достаточно сложны в реализации,
хотя и обеспечивают высокую помехоустойчивость. Наряду с ними широко
применяют более простые алгоритмы. Для этой цели используют класс СК,
допускающих пороговое декодирование.
Рассмотрим систематический код со скоростью 1/2 и многочленами:
Схема кодека на рисунке. Моделью двоичного канала являются сумматоры
модулю 2, на входы которых, кроме кодовых последовательностей а(1) и а(2),
поступают ошибки е(1) и е(2). Декодер содержит аналог кодера, в котором
принятым символам формируется копия проверочной последовательности. В
формирователе синдрома (сумматоре по модулю 2) образуется
последовательность синдромов, которая поступает на вход синдромного
регистра. Наборам ошибок соответствуют определенные конфигурации синдромов
последовательности S. Если количество ненулевых синдромов превышает
определенный порог, на выходе порогового элемента появляется символ
коррекции, который в корректоре используется для исправления ошибки в
Список использованной литературы:
1. Радиотехнические системы передачи информации, под ред. В. В. Калмыкова
2. Сверточные коды в системах передачи информации, учебное пособие
Помехоустойчивое кодирование для передачи цифрового телевидения по каналам связи
Владимир Блох
эксперт
Введение
При увеличении скорости передачи качество передачи оценивалось по BER – отношению количества ошибок по сравнению с количеством переданных бит. Появились понятия «готовность линии к передаче» и «качество передачи». Характеристики качества были приведены в рекомендациях G.811 и G.826 МСЭ-Т. При анализе характеристик качества период времени передачи исключается.
В XX веке появилось понятие «помехоустойчивое кодирование». Оно началось с появлением кодов Хэмминга, формулы и предела Шеннона.
Хотя, может быть, следует вспомнить Евклида, который 3500 лет назад ввел понятие помехоустойчивого кодирования. Определил необходимую скорость передачи символов и дистанцию между ними – «дистанция по Евклиду». Ею пользуются в США и сейчас, применяя TCM-модуляцию (теперь 8PSK – решетка с 8 состояниями), по правилу Унгербоека с пространственной избыточностью. Эффективность кодирования получается 3,6 дБ.
После 50-х годов прошлого века специалисты стали считать, что сбой импульсной посылки происходит не из-за игольчатого выброса шума в 5–10•10 6 пкВт, а из-за белого гауссового шума AWGN (Additive White Gaussian Noise) в канале с релеевскими замираниями.
Априорную вероятность ошибки определяли как:
отношение сигнал/шум на бит (SNR). При М-модуляции формулы имеют более сложный вид. Вероятность ошибки на бит – это вероятность того, что в сообщении из L битов m будут ошибочными.
учитывая, что ошибки при приеме кодовых символов происходят независимо с вероятностью po. При малой вероятности ошибки в канале с учетом скорости кода R = k/n можно считать:
Канальное кодирование позволяет исправлять ошибки цифровой информации за счет включения в поток избыточных импульсов. При этом уменьшается энергия одного бита. Она становится равной K/n.Eb.
Согласование возможности прохождения сигнала через радиотехнические цепи сделал Шеннон. Он предложил формулу, которая теперь носит его имя:
Шеннон показал, что пропускная способность канала C с аддитивным шумом AWGN является отношением средней мощности принимаемого сигнала S к средней мощности шума и ширине полосы пропускания W.
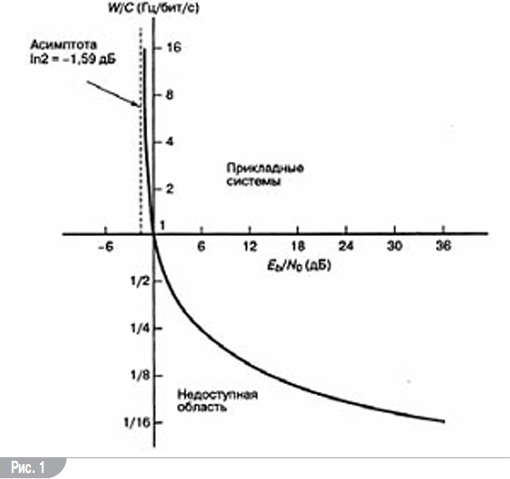
При увеличении спектра сигнала (с К8 на К32 в стандарте Т2) пропускная способность увеличивается. Пропускная способность имеет размерность бит/c. Нижнее предельное значение Eb/N0, при котором ни при какой скорости нельзя осуществить безошибочную передачу информации, называют пределом Шеннона, равным Eb/N0 = 1,6 дБ, где Eb – мощность сигнала на бит; N0 – полоса шума на бит.
На рис. 1 показана зависимость нормированной полосы канала от Eb и N0.
Телевизионный сигнал, выходящий со студии – аналоговый. Превращение его в цифровой осуществляется с помощью теоремы Котельникова. Она приводится в учебниках по телевидению. Поэтому не будем на ней останавливаться.
Первые помехоустойчивые коды предложил Хэмминг. Это были блочные коды, исправляющие одну ошибку. Они записывались так: К(n,k,d), где n число приходящих импульсов, к – информационных. Количество ошибок, которые может исправить код t = (d-1)/2.
Коды могут быть образованы с помощью примитивных полиномов или с помощью матрицы. Пример построения матриц для кода Хэмминга 5.3 приведен ниже.
Система помехоустойчивости состоит из:
Эффективность кодирования
Без кодирования энергия бита была равна Eb, а при блочном кодировании с учетом избыточности будет меньше на k/n. Следовательно, Ebk = k/nEb.
Скорость передачи канальных битов Rc должна превышать скорость передачи Rb в n/k раз.
Символьная передача Rs меньше канальной Rc в (log2M) раз.
Для систем с модуляцией и кодированием преобразование скорости имеет следующий вид:
Преобразование энергии битов в энергию символов связано такими же множителями, что и преобразователи скоростей. Отношение энергии канального бита к спектральной мощности шума Ec/No – это результат умножения Eb/No на коэффициент k/n. Путем умножения Ec/No на коэффициент (log2M) c вычисляется Pe.
Для систем, содержащих одновременно модуляцию и кодирование, преобразование отношения энергии к спектральной плотности мощности шума будет:
Отношение принимаемой мощности к спектральной плотности шума будет:
Синхронизация потока TS
Длительность полинома 1503 байта. Синхронное слово 0х47. Инвертированное синхронное слово 0хB8.
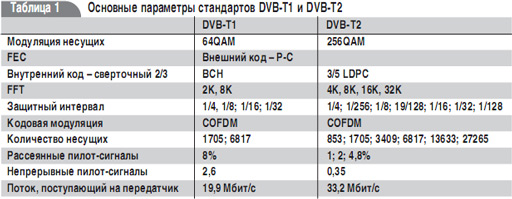
При модуляции QPSK и скорости внутреннего кода – 1/2 обеспечивается самая высокая защищенность при отношении сигнал/шум 3,1 дБ. При модуляции – 64QAM и скорости внутреннего кода 7/8 необходимо иметь соотношение сигнал/шум – 20,1 дБ.
В табл. 1 приведены основные параметры двух стандартов.
Входной поток, поступающий на передатчик, подвергается сжатию по стандарту MPEG-2 или MPEG-4 и превращается в сигналы физического уровня PLPc, которые, расщепляясь, превращаются, в свою очередь, в потоки TS. Предложенная на рис. 1 система предполагает наличие трех составных потоков: SS.1; SS.2; SS.3 (каждый из них содержит кодирование по видео и звуку) и две субсистемы – SS.4 и SS.5. Все это через статистический мультиплексор (statistical multiplexer) объединяется и поступает на межсетевой переход (SS.2 Basic Gateway), затем с него расходятся на свои модуляторы. Потоки трансформируются в RF-каналы и т.д. и поступают на антенну. На приемной стороне потоки детектируются и демодулируются, потом поступают в телевизор.
В стандартах Т1и Т2 в качестве помехоустойчивого кода используется каскадный код Форни. В основе его построения лежит совместное использование двух кодов, состоящих из внешнего кода Рида – Соломона c коэффициентом кодирования R = K/N и внутреннего – сверточного r = k/n. Суммарный коэффициент кодирования равен rR = kK/nN. Причем закодированные символы внешнего кода кодируются кодом внутренним.
Минимальное расстояние каскадного кода D = d1d2, а кодовая скорость равна:
где r1r2 – кодовые скорости.
Коды Рида – Соломона
Коды Рида – Соломона (Р-С) с параметрами (n, k, d), где n = 2 S – 1, формируют один из n символов поля Галуа GF(2S) для каждой группы, содержащей последовательно информационные символы. Коды Р-С называют линейными кодами потому, что они образованы набором блоков фиксированной длины, в которых каждый элемент кодового слова выбирается из алфавита q-символов. Коды Р-С имеют максимально возможные минимальные кодовые расстояния, обеспечивающие наибольшую корректирующую способность по сравнению с другими линейными кодами. Код Р-С с m = mo-1 характеризуется следующими параметрами:
Для детектирования кодов Р-С используют жесткое решение.
Чаще всего коды Р-С используют для передачи цифрового телевидения. При этом код Р-С имеет байтовую структуру, то есть S = 8, nmax = 256. Чаще всего используется код Р-С с параметрами: (204.188,16) или (204,188; t = 8). Полоса пропускания определяется символьной скоростью приходящего потока: Symbol Rate S:
Для 16QAM – m = 4, для 64QAM – 6, 256QAM – 8. Правка ошибок основывается на GHT = 0. Для определения вероятности ошибки при применении кода Рида – Соломона можно воспользоваться приведенной формулой.
Сверточные коды
Сверточные коды (СК) относятся к непрерывным кодам, где передаваемая последовательность не может быть разбита на независимые блоки. При СК дополнительные символы содержатся в последовательности предыдущих.
СК преобразует k0 информационных символов, поступающих на его вход, в n0 выходных кодовых символов, n0> k0. Выходные символы являются линейными комбинациями над полем GF(q) входных символов из предшествующих m блоков. Преимущество СК по отношению к блочным заключается в непрерывном обнаружении и исправлении ошибок. Сверточный код задается параметрами: n, k, К, где k – число входов; n – число выходов; r = k/n – кодовая скорость, K – конструктивная длина кода; ηa – длина кодового ограничения.
Параметрами СК-кода, характеризующими его помехоустойчивость, является минимальное свободное расстояние по Хэммингу между последовательностями сверточного кода по длине кодовых ограничений – deff. Оно определяет эффективность кода при разных значениях его скорости r. Об этом мы поговорим позднее.
Сверточные кодеры бывают несистематические, не имеющие обратных связей, и систематические, с обратными связями.
Выходные символы формируются с помощью рекуррентного соотношения из K информационных символов, поступающих в данный и предшествующие моменты времени. Величина K называется длиной кодового ограничения и играет ту же роль, что и длина блочного кода.
Способы декодирования сверточных кодов представлены.
Внешнее и внутреннее перемещение (3; 4; 5) для стандартов Т1 и Т2 рассмотрены в Л 2.5.
При COFDM-модуляции исходный спектр разделяется на N несущих частот ортогональных подканалов, в каждом из которых осуществляется модуляция последовательностью данных. В K = 8 используется от 64 до 6817 точек преобразования. Важным параметром систем является быстрое преобразование Фурье. Длительность преобразования Фурье составляет от 10 до нескольких сот мкс.
Для уменьшения влияния на приеме многолучевого распространения применяют защитный интервал, во время которого значение принятого символа не определяется. От 1/32 до 1/4 длительности быстрого преобразования Фурье для стандарта Т1.
Защитный интервал – это не просто пауза между полезными символами, достаточная для угасания сигнала символа до начала следующего. Он пропускает часть полезного сигнала, гарантирует сохранение ортогональности несущих принятого сигнала. Величина защитного интервала зависит от расстояния между передатчиками в одночастотных сетях или от задержки естественного эхо-сигнала в сетях вещания. Считают, что она должна содержать четвертую часть от величины полезного интервала.
В режиме OFDM каждый символ формируется одной поднесущей. В приемнике основные шаги процесса демодуляции выполняются в обратном порядке: полученные сигналы во временной области квантуются и поступают в процессор БПФ, который восстанавливает комплексный спектр. Затем спектральные компоненты обрабатываются как отдельные сигналы, для того чтобы декодировать данные, которые мультиплексируются в основной поток данных.
В передающем устройстве роль модулятора выполняет интегральная схема быстрого обратного преобразования Фурье.
В приемном устройстве – прямое преобразование Фурье и процессор, который восстанавливает комплексный спектр. Затем спектральные компоненты обрабатываются в отдельные сигналы для того, чтобы декодировать данные, которые мультиплексируются в основной поток телевидения.
Преобразование Фурье
Преобразование Фурье – это метод обработки, использующийся для анализа изменений сигнала во времени и выражения их в виде спектра.
Длительность преобразования Фурье:
Существенную экономию времени счета дает метод быстрого преобразования Фурье (БПФ), позволяющий сократить число рассчитываемых вариантов с N2 до Nlog2 N. Так, например, при N = 1024 экономия во времени составит около ста раз. Один из алгоритмов БПФ используется при передаче цифрового телевидения. В приемнике основные шаги процесса демодуляции выполняются в обратном порядке.
Основная задача стандарта DVB-T2 – передавать одновременно три программы цифрового телевидения высокой четкости. Поэтому там используют высокоскоростные помехоустойчивые коды.
Внешний код в стандарте Т2-БЧХ Боуза – Чоудхуда – Хоквингема
Этот код был известен и раньше. Применение его откладывалось из-за отсутствия элементной базы, работающей на высоких частотах.
Коды (БЧХ) представляют собой класс линейных циклических кодов, исправляющих кратные ошибки, и являются результатом обобщений кодов Хэмминга. Это обеспечивает свободу выбора длины блока, степени кодирования, размеры алфавита и возможности коррекции ошибок. В кодах БЧХ в случае больших n и кодовые слова записывают в начале последовательности. Например, кодовое слово (Cn-1,Cn-2,+…) в виде полинома C(x) = a(x)g(x). После ряда преобразований и умножения полинома на Xn-k получаем Xn-kb(x)=a(x)g(x)+p(x), где p(x) – полином. Степени не более n-k-1 определят ошибки передачи. Если он равен 0, то ошибок нет.
Коды БЧХ характеризуются следующими параметрами:
N = 2 m-1 ; r – любое; d = 2t + 1; t = (2m-1-k)/m/. Где m – целое положительное число, t – ошибки.
Величина энергетического выигрыша определяется rd (чем больше rd, тем больше выигрыш). БЧХ имеют параметры: n = 2 m – 1; n-k ≤ mt; dmin = 2t + 1.
Вероятности ошибки в кодовом блоке P, q-символе Ps и в бите Pb при декодировании БЧХ по максимуму правдоподобия приведены ниже:
Так как коды БЧХ относятся к циклическим блоковым кодам, задаваемым образующим полиномом, кодирование информационной последовательности осуществляется в соответствии с C(X) = U(X) g(x).
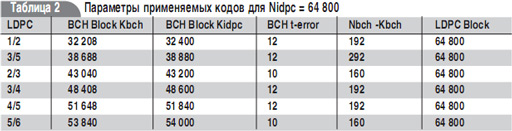
Применение в качестве внешнего кода BCH предложенной длины может исправлять от 10 до 12 ошибок. Двоичные коды БЧХ, порожденные примитивными полиномами поля Галуа GF(gm), меньше 210 могут исправлять несколько ошибок. Например, (255,9) – 63 ошибки. Предложенные в стандарте DVB-T2 длинные коды имеют в своем составе меньше избыточных битов, но при этом усложняется синдром исправления ошибок и увеличивается мощность на их передачу. В табл. 2 для стандарта DVB-T2 представлены параметры применяемых кодов для Nidpc = 64 800. Из них мы заключаем, что избыточность от всех представленных кодов одинакова.
Внутренний код LDPC (Low Density Parity Check codes) с низкой плотностью проверок. Код имеет минимальное расстояние d и поэтому все ошибки могут быть исправлены при почти линейной сложности алгоритма декодирования.
В работах показано, что LDPC-коды могут быть близки к пределу Шеннона. При скорости 1/2 с длиной блока 10000000 код отличается от предела Шеннона 0,0045 дБ.
Регулярный LDPC-код является линейным (n, k), проверочная матрица которого H имеет Хеммингов вес. Столбцы и строки равны J и K соответственно. Причем обе величины меньше длины кода N.
Применяя BCH + LDPC, удается получить выигрыш по сравнению с кодом Р-С + сверточный 5 дБ (рис. 4) DVB BlueBOOK A133. Применение модуляции несущих 256QAM увеличивает емкость канала на треть.
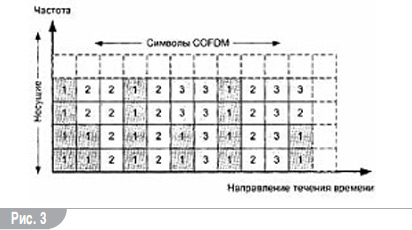
На вход системы поступают потоки от трех независимых программ телевидения высокой четкости (рис. 2). Эти потоки называются phsycal layer pipes (PLP). В DVB-T2 каждый из них помещается в свою PLP. Структура суперфрейма представлена на рис. 3. Программы поступают на передатчик последовательно.
Для одночастотных сетей введен режим MISO Multiple Input Single Output – много входов, один выход.
Количество пилот-сигналов уменьшено (табл. 1).