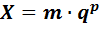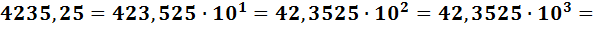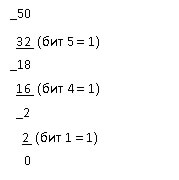как представить число в двоичном коде
Представление чисел в двоичном коде



Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых ячейках памяти. Вся память компьютера разбита на отдельные участки и 8 бит (т.е. на байты). Байты имеют номера: 0, 1, 2, …, называемые адресами. Два соседних участка: 0 и 1, 2 и 3 и т.д. образуют ячейку памяти ЭВМ. Т.е. одна ячейка памяти может хранить два байта или 16 битов информации. Для содержимого одной ячейки используют название – «машинное слово» или просто «слово». Очевидно, адресом числа считается адрес первого байта, т.е. четные числа, начиная с 0, 2, 4, 6 и т.д. В байте может содержаться произвольный код из восьми двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число.
Числа могут быть целые точные, дробные точные, рациональные, иррациональные, дробные приближенные, положительные и отрицательные. Числа могут быть «карликами» (например, масса атома), «гигантами» (например, масса земли), реальными (например, количество студентов в группе, рост, возраст). И каждое из чисел потребует для оптимального представления в памяти свое количество байтов.
Единого оптимального представления для действительных чисел создать невозможно. Поэтому множества чисел разделили на типы (например, целые в диапазоне от … до …, приближенные с плавающей точкой с количеством значащих цифр … и т.д.). Для каждого в отдельности типа создается собственный способ представления.
Целые числа. Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера.
| Числа | Двоичный код |
| … | …….. |

В дополнительном коде хорошо реализуется арифметика. Каждый последующий код получается из предыдущего прибавлением единицы с точностью до бита в девятом разряде. Например, 5 – 3 = 5 + (-3)

Отбрасывая подчеркнутый старший разряд, получим 2.
Аналогично целые числа от 0 до 65536 и целые числа от –32768 до 32767 в двоичной (шестнадцатеричной) системе счисления представляются в двухбайтовых ячейках. Существуют представления целых чисел и в четырехбайтовых ячейках.
Действительные числа. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако, в компьютере числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные. В большинстве систем программирования целая и дробная части в написании действительных чисел разделяются не запятой, а точкой.
Для представления действительных чисел, как очень маленьких, так и очень больших, удобно использовать форму записи чисел в виде произведения:
Где m- основание системы счисления;
P – целое число, называемое порядком.
Такой способ записи чисел называется представлением числа с плавающей точкой.
Т.е. число 1234,56 может быть записано:
Такое представление не однозначно. Если мантисса 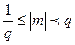
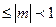
Действительные числа в компьютерах различных типов записываются по-разному, но существует несколько стандартных международных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере 4 байтного числа.
 | |
| Смещенный порядок | Мантисса |
Первый разряд представления используется для записи знака мантиссы. За ним – группа разрядов, определяющих порядок, а остальные разряды определяют абсолютную величину мантиссы. Размеры обеих групп разрядов фиксируются. Т.к. порядок может быть положительным или отрицательным, нужно решить проблему его знака. Величина порядка представляется с избытком, т.е., вместо истинного значения порядка хранится число, называемое характеристикой (или смещенным порядком). Для получения характеристики надо к порядку прибавить смещение. Например, при использовании для хранения порядка восьми бит и значений от –128 до +127 используется смещение 128. Тогда для представления порядка будут использоваться значения от 0 до 255, т.е. только неотрицательные числа.
Т.к. мантисса нормализованного числа всегда равна 1, некоторые схемы представления ее лишь подразумевают, используя лишний разряд для повышения точности представления мантиссы.
Использование смещенной формы позволяет производить операции над порядками, как над без знаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков. А также упрощает операцию сравнения самих нормализованных чисел. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего, отличного от нуля числа до наибольшего числа, представимого в компьютере при заданном формате.
Как и в случае целых чисел, в программных системах могут использоваться несколько типов данных, реализующих модель с плавающей точкой. Например, в языке СИ применяются три типа данных с разной «длиной». Шестнадцатиразрядные компиляторы для IBM-совместимых ПК реализуют эти типы следующим образом:
Float – 4 байта, из них 23 разряда мантиссы и 8 битов порядка
Double – 8 байтов, из них 52 разряда мантиссы и 11 битов порядка
Long double – 10 байтов, из них 65 разрядов мантиссы и 14 битов порядка
Понятие типа данных. Мы уже говорили, что минимально адресуемой единицей памяти является байт, но представление числа требует большего объема. Такие числа займут группу байт, а адресом числа будет адрес первого байта группы. Следовательно, произвольно взятый из памяти байт ничего не скажет о том, частью какого информационного объекта от является – целого числа,числа с плавающей точкой или командой. Отсюда можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача – интерпретации кодов, т.е. как из кодов восстановить первоначальные данные.
Для представления основных видов информации (числа целые, числа с плавающей точкой, символы, звук и т.д.) в системах программирования используют типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных.
Представление чисел в двоичном коде. Дополнительный код
Целые числа.
Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера.
В такой форме представления легко реализуется на компьютерах двоичная арифметика.
Если нужны и отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит; ноль интерпретируется как плюс, единица как минус. В таком случае одним байтом может быть закодированы целые числа в интервале от —127 до +127. Рассмотренный способ представления целых чисел называется прямым кодом. Положение с отрицательными числами несколько упрощается, если использовать, так называемый, дополнительный код. В дополнительном коде положительные числа совпадают с положительными числами в прямом коде, отрицательные же числа получаются в результате инверсии всех битов числа и добавлении единицы к младшему левому разряду. Например, число 
При представлении отрицательных чисел в дополнительном коде операция вычитания заменяется операцией сложения. Например,
Отбрасывая подчеркнутый старший разряд, получим
Действительные числа. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако в ЭВМ числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в ЭВМ выступают как приближенные.
Для представления действительных чисел большой и малой разрядности удобно использовать форму записи чисел в виде произведения
где 


Такой способ записи чисел называется представлением числа с плавающей запятой. Число 4235,25 может быть записано в одном из видов:
Если мантисса для десятичной системы счисления

либо же для двоичной
то представление числа становится однозначным, а такая форма называется нормализованной. Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т.е. максимальная точность.
Действительные числа в ЭВМ различных типов записываются по-разному, тем не менее существует несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере числа, занимающего 4 байта.
Первый бит двоичного представления используется для кодирования знака мантиссы. Следующая группа бит кодирует порядок числа, а оставшиеся биты кодируют абсолютную величину мантиссы. Длины порядка и мантиссы фиксированы.
Порядок числа – целые числа, могут быть как положительными, так и отрицательными. Чтобы отразить в двоичной форме, величина порядка представляется в виде суммы истинного порядка и константы, равной абсолютной величине максимального по модулю отрицательного порядка, называемой смещением. Например, если порядок может принимать значения от —128 до 127 (8 бит), тогда, выбрав в качестве смещения 128, можно представить диапазон значений порядка от 0 (-128+128, порядок + смещение) до 255 (127+128).
Так как мантисса нормализованного числа всегда начинается с нуля, некоторые схемы представления его лишь подразумевают, используя лишний разряд для повышения точности представления мантиссы. Использование смещенной формы позволяет производить операции над порядками как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.
Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, пред ставимого в компьютере при заданном формате.
Вещественные числа в памяти компьютера, в зависимости от требуемой точности (количества разрядов мантиссы) и диапазона значений (количества разрядов порядка), занимают от четырех до десяти байтов. Например, четырехбайтовое вещественное число имеет 23 разряда мантиссы (что соответствует точности числа 7—8 десятичных знаков) и 8 разрядов порядка (обеспечивающих диапазон значений 10±38). Если вещественное число занимает десять байтов, то мантиссе отводится 65 разрядов, а порядку — 14 разрядов. Это обеспечивает точность 19—20 десятичных знаков мантиссы и диапазон значений 10±4931.
Число двойной точности (для 32-разрядны ЭВМ – 64 бита или 8 байт)
Понятие типа данных
Как уже говорилось, минимально адресуемой единицей памяти является байт, но представление числа требует большего объема. Очевидно, такие числа займут группу байт, а адресом числа будет адрес первого байта группы. Следовательно, произвольно взятый из памяти байт ничего нам не скажет о том, частью какого информационного объекта он является — целого числа, числа с плавающей запятой или команды. Резюмируя вышесказанное, можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача — задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные. Для представления основных видов информации (числа целые, числа с плавающей запятой, символы, звук и т.д.) в системах программирования используют специального вида абстракции — типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных. В дальнейшем для каждого типа данных будут определены и соответствующие ему операции обработки.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Как представить число в двоичном коде
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
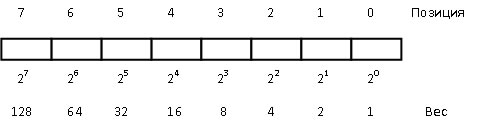
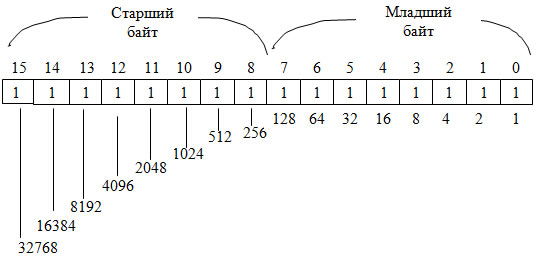
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Дубликаты не найдены
Большое спасибо! Очень хорошо объяснили. Всё понял.
Берем калькулятор и перемножая двойку саму на себя подбираем максимально близкое (но меньшее 85) число
Повторяем операцию для 21
Ближайшее 16, или 2 в 4 степени
Ближайшее 4, или 2^2
1, или 2 в степени 0.
Теперь собираем наше число, проставляя единицу для той степени двойки, которая у нас встретилась (т.е. 2^6 2^4 2^2 2^0) и нуль для той степени, которая не встрети лась (2^5 2^3 2^1)
2^6 2^5 2^4 2^3 2^2 2^1 2^0
спасибо, оч доступно)
Вот этот абзац объясняет принцип записи:
——
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
——
Можете в качестве обратной связи рассказать, что именно здесь не ясно? 🙂
«не хватает перевода из десятичной в двоичную»
Да, я уже осознал этот изъян и подготовил пост про перевод из десятичной в двоичную. Завтра выложу. 🙂
«и остальных операций двоичной арифметики»
Мне показалось, что для чайников это сложновато уже. Мне лично как программисту крайне редко приходится делать с двоичным кодом что-то из арифметики, кроме сложения.
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]= 100 «
и еще «= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
поделитесь, пожалуйста, еще постами по информатике если есть
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
А теперь слушайте домашнее задание: построить синхрофазотрон.
Да просто.
6 = 1х2^2 +1х 2^1 + 0х2^0 = 110
7 = 1х2^2 + 1×2^1 + 1×2^0 = 111
7 = 4 +3 +1 = 100 + 010 + 001
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Ну, мы числа называем в десятичной системе, поэтому в простых случаях двоичное число переводят в десятичную в уме и так читают. 🙂
Ну ты же не называешь число В в HEX «одиннадцать», хотя оно именно 11?
Ну, и «B» я прочитаю как «одиннадцать» или как «бэ» в зависимости от контекста 🙂
Ну да. Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?
«Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?»
Не очень понял вопрос. Что с чем я должен путать, по-твоему?
«Ну а в двоичной системе, по которой ты строишь счет, понятия «два» не существует.»
Я утверждаю, что у многих чисел есть названия. И так сложилось исторически, что эти названия даны в десятичной системе.
Например, если я в унарной системе запишу:
111 + 1111 = 1111111
Я буду читать «три плюс четыре равно семь», а не «сто одиннадцать плюс тысяча сто одиннадцать равно один миллион сто тысяч. «.
Ты называл число В как 11, не смотря на то, что у тебя есть в этой же системе 11, эквивалентное десятичной 17.
Сбивает с толку? Да не больше, чем её графическая запись.
если с двоичной системы такие названия к проблемам восприятия могут и не привести, то в шестнадцатеричной точно будет путаница.
Держи мое объяснение:
Когда ты считаешь до десяти, у тебя в какой-то момент кончаются названия чисел и тебе приходится комбинировать названия, чтобы считать больше 9. Например:
Ну а в двоичной системе цифры кончаются уже после 1, так и живем:
Как ты понимаешь, от того, как мы назвали количество, само количество от этого не изменилось, изменился только способ счета.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
Неправильные примеры. Да и как такового знака + и * в булевой алгебре нет
На самом деле все еще проще.
нет есть способ проще, всмысле рассказать
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
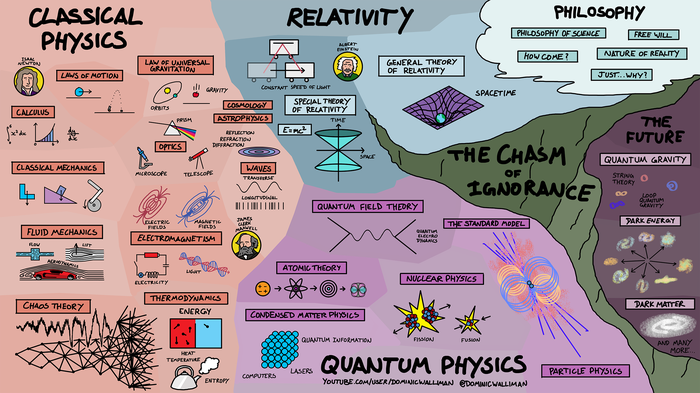
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.