как расшифровывается двоичный код
Как читать двоичный (бинарный) код
Если вам интересно узнать, как читать двоичные числа, важно понять, как работают двоичные числа. Двоичная система известна как система нумерации «base 2», что означает наличие двух возможных чисел для каждой цифры; один или ноль. Большие числа записываются путем добавления дополнительных двоичных единиц или нулей.
Понимание двоичных чисел
Знание того, как читать двоичные файлы, не является критичным для использования компьютеров. Но хорошо понять концепцию, чтобы лучше понять, как компьютеры хранят числа в памяти. Он также позволяет понимать такие термины, как 16-битные, 32-битные, 64-битные и измерения памяти, такие как байты (8 бит).
Как читать двоичный код
«Чтение» двоичного кода обычно означает перевод двоичного числа в базовое 10 (десятичное) число, с которым люди знакомы. Это преобразование достаточно просто выполнить в своей голове, когда вы поймете, как работает бинарный язык.
Каждая цифра в двоичном числе имеет определенное значение, если цифра не является нулем. После того как вы определили все эти значения, вы просто складываете их вместе, чтобы получить 10-значное десятичное значение двоичного числа. Чтобы увидеть, как это работает, возьмите двоичное число 11001010.
2. Затем перейдите к следующей цифре. Если это один, то рассчитайте два в степени одного. Запишите это значение. В этом примере значение равно степени два, равной двум.
3. Продолжайте повторять этот процесс, пока не дойдете до самой левой цифры.
4. Чтобы закончить, все, что вам нужно сделать, это сложить все эти числа вместе, чтобы получить общее десятичное значение двоичного числа: 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202.
Двоичные числа с подписью
Приведенный выше метод работает для базовых двоичных чисел без знака. Однако компьютерам нужен способ представления отрицательных чисел также с помощью двоичного кода.
Из-за этого компьютеры используют двоичные числа со знаком. В системе этого типа самая левая цифра известна как знаковый бит, а остальные цифры известны как биты амплитуды.
Чтение двоичного числа со знаком почти такое же, как и без знака, с одним небольшим отличием.
1. Выполните ту же процедуру, как описано выше для двоичного числа без знака, но остановитесь, как только вы достигнете самого левого бита.
2. Чтобы определить знак, осмотрите крайний левый бит. Если это единица, то число отрицательное. Если это ноль, то число положительное.
4. Бинарный метод со знаком позволяет компьютерам представлять числа, которые являются положительными или отрицательными. Однако он потребляет начальный бит, а это означает, что для больших чисел требуется немного больше памяти, чем для двоичных чисел без знака.
Двоичный код.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.
На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.
Перевод натурального числа десятичной системы счисления в двоичную систему.
Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:
1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.
2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.
3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.
4. В этот момент считается, что двоичный код готов.
Для примера переведем в двоичную систему число 7:
1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.
2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.
3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.
4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.
Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.
Перевод числа двоичной системы в десятичную.
Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.
Немного из истории двоичной системы счисления.
Значение двоичного кода – почему компьютеры работают с единицами и нулями
Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
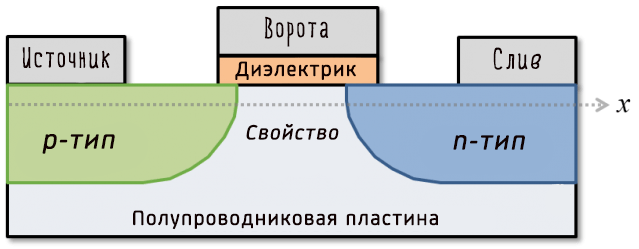
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
Вот схема типичного транзистора:
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
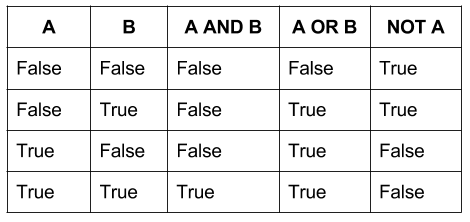
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.
Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.
Как расшифровывается двоичный код?
Просто число. Например, 00000001 — это число «1» записанное в двоичном виде. 00000010 — это двойка, 00000011 — это тройка и т.
Как научиться читать двоичный код?
Как читать двоичный код
Какие числа можно отнести к двоичному коду?
— число разрядов двоичного кода. Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
Почему двоичный код?
Значение двоичного кода – почему компьютеры работают с единицами и нулями … Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате. Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять.
Какие коды называются двоичными приведите примеры?
BCD — это способ выразить каждую десятичную цифру двоичным кодом. В BCD с четырьмя битами мы можем представить шестнадцать чисел (от 0000 до 1111). Но в коде BCD используются только первые десять из них (от 0000 до 1001). Остальные шесть кодовых комбинаций, то есть 1010–1111, недопустимы в BCD.
Что такое разряд двоичного кода?
д. Длину двоичной цепочки — количество символов в двоичном коде – называют разрядностью двоичного кода. … Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так: N=2i.
Что такое восьмиразрядный двоичный код?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код просто порядковый номер символа в двоичной системе счисления.
Кто придумал двоичный код?
Первые методы похожие на двоичную систему появились еще в Древнем Китае и Индии. Основы современной двоичной системы исчисления были заложены в работах Фрэнсиса Бэкона, Карла Лейбница (17-й век) и Джорджа Буля (19-й век). Именем последнего названа Булевая логика которая также применяется в программировании.
Как найти разрядность двоичного кода?
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так: В математике такие произведения записывают в виде: N = 2i. Запись 2i читают так: «2 в i-й степени».
Для чего используется двоичное кодирование?
Двоичное кодирование – один из распространенных способов представления информации. В вычислительных машинах, в роботах и станках с числовым программным управлением, как правило, вся информация, с которой имеет дело устройство, кодируется в виде слов двоичного алфавита. Двоичный алфавит состоит из двух цифр 0 и 1.
Почему персональный компьютер работает с двоичным кодом?
Любая информация в ЭВМ представляетя в виде двоичных кодов. Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.
Как называют количество символов в двоичном коде?
Количество символов (цифр) в алфавите позиционной системы счисления называется основанием системы счисления. Например, система с основанием 2 (=двоичная система счисления) содержит две цифры: 0 и 1.
Почему компьютер работает в двоичной системе счисления?
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям: Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями.
Сколько максимально кодовых комбинаций позволяет получить четырехразрядный двоичный код?
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный — 32, шестиразрядный — 64 и т. д.
Что является результатом кодирования?
Кодирование – процесс присвоения условных обозначений, результатом которого является создание кодов объектов. … структуры кода, т. е.
Сколько максимально кодовых комбинаций позволяет получить восьмиразрядный двоичный код?
Разрядность двоичного кода ( i ) и количество возможных кодовых комбинаций ( N ) связаны соотношением: 2 в степени i = N. Восьмиразрядный двоичный код позволяет получить 256 различных кодовых комбинаций: 2 в степени 8 = 256.
Можно сохранять текстовые данные. В этом случае каждое простое число из предыдущего шага по специальной таблице символов (например, ASCII) сопоставляется с буквой. Например, 01100001 = 97 = «a» (маленькая латинская буква а). 01100010 = 98 = «b» и так далее. Именно этот тип преобразования мы используем.
Есть и более сложный вариант. Когда бинарные данные обрабатываются специальным образом в зависимости от того, что это за файл. Примеры бинарных файлов: файл любой программы, архива, mp3 трек. Просто так их содержимое не просмотреть, вместо этого стоит поискать ту программу, которая сможет работать именно с этим типом файлов.
Дубликаты не найдены
Автор иди преподавать в высшую школу программирования. А лучше обучать шифровальщиков для спецслужб.
512 256 128 64 32 16 8 4 2 1
1 0 0 0 0 1 0 0 0 1 = 1000010001 = 512+16+1 = 529
0 0 0 0 0 0 0 1 1 1 = 0000000111 = 4+2+1 =7
Автор получает свой заслуженный минус
Расшифруй это и познаешь дзен
Кто бы рассказал, каким образом вот эта вот последовательность из 0 и 1 превращается в действия компа. Нет, мне не надо сейчас про архитектуру затирать и прочие радости. Мне интересно, каким образом набор транзисторов (условно) в виде процессора обрабатывает и перенаправляет поток сигналов между компонентами.
О коде
Проект Семь пятниц на неделе #217. День программиста в високосные годы
Конечно же это просто юмор. И вообще очень интересно наблюдать, как 15 лет назад все угарали с «компьютерщиков» и помногу раз пересказывали шутеечки формата «в ванной нашли труп программиста с пустой бутылкой от шампуня, на которой было написано: намылить, смыть, повторить» и «программист перед сном ставит на тумбочку два стакана — с водой и пустой, первый на случай если захочется пить, а второй — если не захочется». А еще 15 лет назад все родители хотели видеть своих чад выпускниками юридических и экономических вузов. А теперь те самые «компьютерщики» правят миром, и пишут программное обеспечение, которое скоро заменит тех самых юристов и экономистов. Вон, года три-четыре назад Сбер анонсировал увольнение штата юристов и замены их нейросеткой.
Я каждый день с 8 февраля рисую по комиксу, связанному с событием произошедшим в эту дату, когда она была пятницей! Если хотите поддержать меня, то вот — http://desvvt.art/
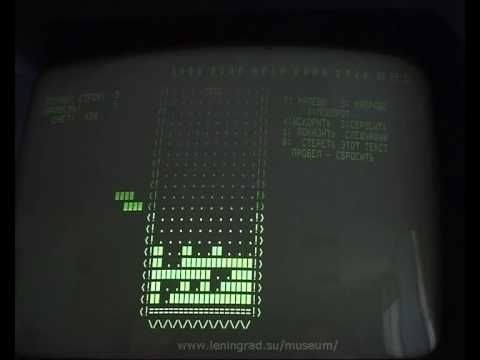
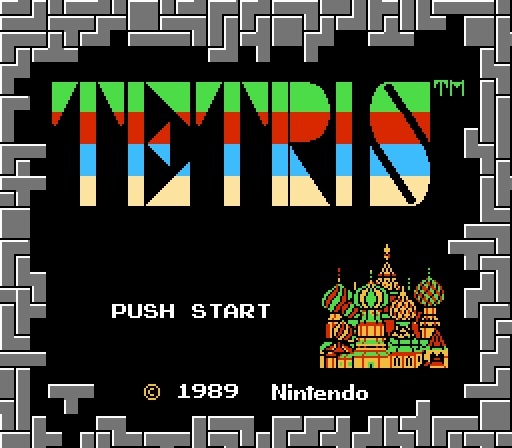
День рождения Тетриса
Tetris: From Russia With Love
6 июня 1984 года — советский программист Алексей Пажитнов представил компьютерную игру «Тетрис». Множество производителей видеоигр сделали на ней миллионы. За продажу лицензии Пажитнов получил один IBM-совместимый компьютер 286-й модели.
Интерес к фигурам домино, тримино, тетрамино и пентамино в СССР возник благодаря книге С. В. Голомба «Полимино» (издательство «Мир», 1975 год).
В частности, пентамино было настолько популярно, что в «Науке и жизни» начиная с 1960-х годов был постоянный раздел, посвящённый составлению фигурок из набора пентамино, а пластмассовые наборы пентамино иногда продавались в магазинах.
«Тетрис» был впервые написан Алексеем Пажитновым в июне 1984 года на компьютере Электроника-60. Работая в ВЦ Академии наук СССР, Пажитнов занимался проблемами искусственного интеллекта и распознавания речи, а для обкатки идей применял головоломки, в том числе и классическое пентамино. Пажитнов пытался автоматизировать укладку пентамино в заданные фигурки. Однако вычислительных мощностей тогдашнего оборудования для вращения пентамино не хватало, приходилось отлаживать на тетрамино, что и определило название игры. В тех опытах и родилась основная идея «Тетриса» — чтобы фигурки падали, а заполненные ряды исчезали.
Для IBM PC игра была переписана на Turbo Pascal 16-летним школьником Вадимом Герасимовым. Игра быстро распространилась по Москве и далее по всему миру.
Несколько месяцев спустя про игру узнал импортер программного обеспечения из Венгрии — Роберт Стейн.
Стейн поехал в Москву, где он встретился с Алексеем Пажитновым, и договорился о лицензии на выпуск игры. По какой-то неизвестной для Стейна причине Пажитнов подарил ему тетрис. Роберт Стейн сразу решил, что игру можно было свободно издавать.
В 1988 году разработчик и издатель игр нидерландского происхождения Хенк Роджерс занимался ввозом новых игр в Японию. Он познакомился с тетрисом в 1988 году на выставке бытовой электроники в Лас-Вегасе. Он ходил по выставкам, покупал понравившееся ему игры и привозил их в Японию, где их издавали не платя за лицензию. Хенк поиграл в тетрис и ушел, потом вернулся, опять поиграл и ушел, потом опять вернулся и поиграл — игра затягивала.
Стейн продал права на «Тетрис» компании Mirrorsoft (и её дочерней компании Spectrum HoloByte), принадлежащей британскому медиа-магнату Роберту Максвеллу. У игры появляются качественные по меркам того времени графика и звук, а также «русский колорит» — в фоновых заставках программы появляются Юрий Гагарин, Матиас Руст, незадолго до этого совершивший посадку своего спортивного самолета на Красной площади, и другие подобающие случаю персонажи. На глазах рождается сенсация — первая игра из-за «железного занавеса».
Вполне возможно, что о Пажитнове так бы никто и не узнал, если б не пронырливость журналистов CBS, представивших всему миру настоящего автора популярной игры.
Spectrum Holobyte и Mirrorsoft на условиях сублицензирования продают права на разработку консольных версий «Тетриса» соответственно фирмам Bullet-Proof Software и Atari Games. При этом первая получает возможность разрабатывать программы только для систем, продающихся на японском рынке. Условия второй гораздо выгоднее — её «зона ответственности» включает Японию и США.
В 1989 году в Nintendo полным ходом идет разработка карманного игрового компьютера Game Boy. Глава американского отделения фирмы Минору Аракава (Minoru Arakawa) убеждает президента Bullet-Proof Software Хенка Роджерса (Henk Rogers) вступить в переговоры со Стейном по поводу возможности разработки версии «Тетриса» для Game Boy.
Nintendo от продажи игры получила очень неплохие прибыли, но сам Алексей Пажитнов смог воспользоваться плодами своего детища только в 1996 году, когда истёк срок первоначальной лицензии, и он начал получать первые (весьма небольшие) отчисления от продаж.
В 1996 году он с Хенком Роджерсом (англ. Henk Rogers) создал компании The Tetris Company LLC и Blue Planet Software, пытаясь получить прибыль от бренда Tetris. The Tetris Company LLC (TTC) зарегистрировала слово Tetris как торговую марку. С тех пор несколько компаний купили у TTC лицензию на торговую марку, но законность игр тетрамино, которые не используют название Tetris, не оспаривалась в суде. По американским законам, игру нельзя защитить авторским правом (только запатентовать), поэтому основным имуществом компании является торговая марка Tetris. Несмотря на это, TTC преследует клоны игры под именами, непохожими на Tetris. В мае 2010 года юрист TTC послал письмо в Google с требованием убрать с рынка Android Market все 35 клона данной игры, хотя их имена не схожи с именем «Tetris».
В 1996 году Алексей Пажитнов устроился на работу в Microsoft, где под его руководством был выпущен набор головоломок Pandora’s Box.
Сейчас непосредственно программированием Алексей Пажитнов уже давно не занимается, он работал в подразделении Microsoft разработчиком компьютерных игр с 1996 по 2005 год.
29 июня 2010 года, в интервью журналистам одного из геймерских порталов, Алексей Пажитнов сказал, что последние десять лет он работал над многопользовательским режимом для своего детища. Но ещё не закончил.
Слово «тетрис» происходит от греческого «tetra» — четыре, поскольку все фигуры в игре состоят из четырех элементов, скрещенного со словом «теннис». Также существует модификация игры — Пентикс, (от греч. «penta» — пять), в которой фигуры могут состоять из элементов в количестве от одного до пяти.
Вариаций тетриса достаточно много, в том числе трехмерный тетрис, n-мерный тетрис, Polytope Tetris и прочие модификации, со вводными элементами. Идея восходит к старым развлечениям с тетрамино, то есть Пажитнов как бы не на пустом месте его придумал. Что, впрочем, не умаляет гениальности сей затеи.
Основная суть игры — заполнить как можно больше линий блоками тетрамино, не достигнув верхней части экрана. Все заполняемые линии будут удаляться. Игра, теоретически, является бесконечной, а практически — рано или поздно конец игры неминуемо настанет. Но особо трагичный конец случается когда садятся батарейки!
Если играть в тетрис какое-нибудь значимое время (часа 4), а потом лечь спать, то игра удивительным образом продолжается из-за одноименного эффекта.
В Америке ходили слухи, что тетрис был советским планом коммунистов для подрыва производительности американского труда.