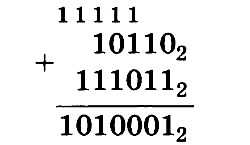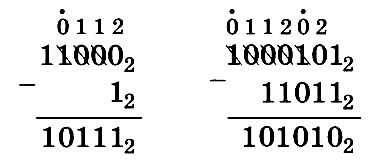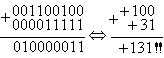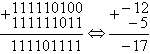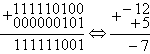как складывать двоичный код

Урок 5
§8. Двоичная система счисления

Содержание урока

Арифметические действия

Арифметические действия

Компьютер выполняет все вычисления в двоичной системе. Разберём, как он это делает, на примере сложения и вычитания.

Вспомните, как выполняется сложение в столбик в десятичной системе счисления. С какого разряда начинается сложение? Когда происходит перенос в следующий разряд?
Как вы думаете, когда будет происходить перенос в следующий разряд при сложении в двоичной системе счисления?

Двоичные числа, как и десятичные, можно складывать в столбик, начиная с младшего разряда. При этом используют следующие правила (таблицу сложения):

0 + 0 = 0, 1 + 0 = 1, 1 + 1 = 2 = 10₂, 1 + 1 + 1 = 3 = 11₂.

В двух последних случаях, когда сумма 2 = 10₂ или 3 = 11₂ не может быть записана с помощью одного двоичного разряда, происходит перенос в следующий разряд (как в десятичной системе, когда сумма получается больше, чем 9).

Например, сложим в столбик 10110₂ и 111011₂. Единицы сверху обозначают перенос из предыдущего разряда:

Сложите числа, записанные в двоичной системе счисления:

1011101₂ + 110111₂

Проверьте решение, переведя слагаемые и результат в десятичную систему счисления.

Вычитание выполняется почти так же, как и в десятичной системе.

Вот основные правила вычитания в двоичной системе:

В последнем случае приходится брать заём из предыдущего разряда.

Когда берётся заём в двоичной системе счисления, в «рабочий» разряд добавляется уже не 10, а 10₂ = 2 (основание системы счисления), а все «промежуточные» разряды (между «рабочим» и тем, откуда берется заём) заполняются единицами — старшей цифрой двоичной системы счисления. Например:

Выполните вычитание в двоичнои системе счисления:

1011101₂ — 110111₂

Проверьте решение, переведя исходные числа и результат в десятичную систему счисления.

Вспомните, как вычитают из меньшего числа большее в десятичной системе счисления. Используя тот же принцип, выполните вычитание в двоичной системе счисления:

Проверьте решение, переведя исходные числа и результат в десятичную систему счисления.

Следующая страница Недостатки двоичной системы счисления

Cкачать материалы урока

Источник

Системы счисления. Арифметические действия в двоичной системе счисления

Цель: научить учащихся выполнять арифметические действиями в двоичной системе счисления.
Задачи:
образовательные:
— повторение и закрепление знаний учащихся о системах счисления;
— формировать у школьников умение выполнять правильно арифметические действия в двоичной системе счисления;
развивающие:
— развивать логическое мышление учащихся;
— развивать познавательный интерес учеников.

Содержание нового материала: правила сложения, умножения, вычитания и деления в двоичной системе счисления.

Ход урока.

Изучение нового материала.
Правила сложения:
0+0=0
0+1=1
1+0=1
1+1=10
Обратить внимание учащихся на то, что при сложении двух единиц в двоичной системе счисления в записи получается 0, а единица переносится в следующий разряд. При сложении трех единиц получается в записи 1, и единица переносится в следующий разряд. (1+1+1=11).

Пример 1.
101+10=111

Пример 2.
10011+11=1110

Учащиеся самостоятельно решают следующие примеры:
1001+11=1100
110+110=1100

Правила умножения:
0*0=0
0*1=0
1*0=0
1*1=1

Пример 1.
101*11=1111

Пример 2.
1011*101=110111

Учащиеся самостоятельно решают следующие примеры:
1001*101=101101
1001*11=11011

Правила вычитания:
0-0=0
1-0=1
1-1=0
0-1=-1
Обратить внимание учащихся на то, что «минус» в последнем правиле обозначает – «занять разряд (1)».

Пример 1.
10110-111=1111

Объяснение:
Вычитание выполняется так же, как в математике. Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания необходимо занять разряд (1), т.к. 10-1=1. Если слева от такого вычитания стоит 0, то мы не можем занять разряд. В этом случае разряд занимаем в уменьшаемом у близстоящей слева от данного вычитания единицы. При этом все нули, у которых мы не могли занять разряд, необходимо поменять на единицу, т.к. 0-1=-1. Желательно все изменения в цифрах записывать сверху данного вычитания. Дальнейшее вычитание выполнять с получившимися сверху цифрами.

Пример 2.
100000-11=11101

Учащиеся самостоятельно решают следующие примеры:
100010-100=
101011-10111=

Правило деления:
Деление выполняется по правилам математики, не забывая, что мы выполняем действия в двоичной системе счисления.

Пример 1.
101101:1001=101

Источник

Арифметические операции над двоичными числами

Дата добавления: 2015-08-31 ; просмотров: 5623 ; Нарушение авторских прав

1.1. Сложение положительных двоичных чиселвыполняется в обычном двоичном коде, называемым прямым кодом. Один или два старших разряда используются для знака числа. Рассмотрим на примере восьми битного числа с двумя знаковыми разрядами. Использование для представления знака числа двух бит предоставляет интересную возможность контролировать переполнение при выполнении арифметических операций. Рассмотрим несколько примеров.

Просуммируем числа A=12 и B=5. Для выполнения этой операции в АЛУ надо со входов мультиплексоров передать числа A и B без изменения в сумматор, на выходе S, которого получим результат.

В результате суммирования получается правильный результат. Это можно проконтролировать по старшему разряду знака (флагу переноса C), который совпадает со вторым знаковым разрядом (знаком результата).

Просуммируем числа 100 и 31

В этом примере видно, что в результате суммирования произошло переполнение восьмибитовой переменной, т.к. в результате операции над положительными числами получился отрицательный результат. Однако если рассмотреть флаг переноса, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции «исключающее ИЛИ» над старшим битом результата и флагом переноса C. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.

1.2. Сложение отрицательных двоичных чисел выполняетсяв дополнительном коде. В нем операции с отрицательными числами выполняются аналогично операциям с положительными числами.

В примере флаг переноса C тоже совпадает со знаком результата, то есть переполнения не произошло и в этом случае.

В этом примере при суммировании положительного и отрицательного числа автоматически получается правильный знак результата. В данном случае знак результата отрицательный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было.

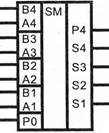
Рис. 1. Обозначение сумматора на функциональных схемах

По выполняемым функциям различают: полусумматоры, одноразрядные сумматоры, многоразрядные сумматоры.

На основе сумматоров строятся арифметико-логические устройства (АЛУ).

Источник