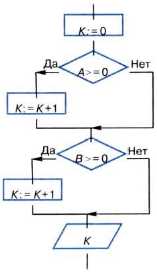
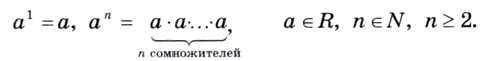какие ключевые слова не могут быть использованы в коде процедуры структуры следование
Базовые структуры алгоритмов
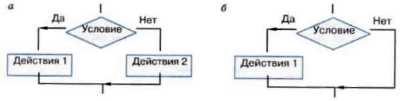
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление и цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
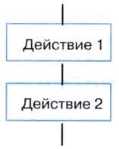
Базовая структура «следование»
Образуется последовательностью действий, следующих одно за другим:
В линейном вычислительном процессе все операции выполняются последовательно в порядке их записи. Типовым примером такого процесса является стандартная вычислительная схема, состоящая из трех этапов:
q ввод исходных данных;
q вычисление по формулам;
q вывод результата.
Базовая структура «ветвление»
Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует в четырех основных вариантах:
| Запись псевдокодом | Графическое изображение |
| 1. Если-то | |
| если условието действия все |  |
| 2. Если-то-иначе | |
| если условие то действия 1 иначе действия 2 все |  |
| 3. Выбор | |
| выбор при условие 1: действия 1 при условие 2: действия 2. при условие N: действия N все |  |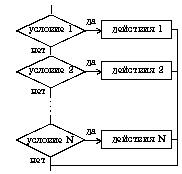
| 4. Выбор-иначе | |
| выбор при условие 1: действия 1 при условие 2: действия 2. при условие N: действия N иначедействия N+1 все |  |
Базовая структура «цикл»
Обеспечивает многократное выполнение некоторой совокупности действий, называемых телом цикла. Управление повторением цикла осуществляется с помощью переменной, называемой параметром цикла. Сначала этому параметру присваивается некоторое начальное значение, затем цикл выполняется с изменением параметра при каждом повторении от начального к конечному значению на величину, называемую шагом цикла.
Шаг цикла может быть положительным или отрицательным. В зависимости от этого параметр цикла возрастает или уменьшается. Цикл прекращается, если параметр цикла принимает значение, которое лежит вне границ диапазона между начальным и конечным значениями.
Различают три вида циклов:
Циклы с предусловием и постусловием используются тогда, когда предварительно неизвестное количество повторений.
В цикле с предусловием сначала проверяется условие и, если оно выполняется, то осуществляются действия, указанные в теле цикла. Выполнение цикла прекращается, когда условие не выполняется. Для этого необходимо, чтоб действия в теле цикла влияли на изменение условия. В противном случае наступит «зацикливание» — бесконечное выполнение цикла. Оно является типовой ошибкой в случае использования циклов.
| Запись псевдокодом | Графическое изображение |
| 1. Цикл с предусловием (Цикл-Пока). Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова «пока». | |
| нц пока условие тело цикла (последовательность действий) кц |  |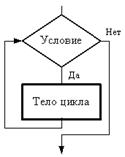
| 2. Цикл с постусловием (Цикл-До). Предписывает выполнять тело цикла до тех пор, пока не выполняется условие, записанное после слова «до». | |
| нц повторять тело цикла (последовательность действий) до условие Кц |  |
| 3. Цикл с параметром (Цикл-Для). Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне | |
| нц для i от i1до i2 шаг i3 тело цикла (последовательность действий) кц |  |
Цикл с постусловием выполняется аналогично, но условие проверяется после выполнения действий в теле цикла. Повторение действий тела цикла происходит тогда, когда условие не выполняется.
Действия в теле цикла с постусловием выполняются всегда хотя бы один раз, а с предусловием могут не выполняться ни одного раза, если в самом начале условие не выполняется.
В цикле с параметром последовательно выполняются следующие типовые операции:
1. Задание начального значения используемого параметра цикла (например, если переменной цикла является i, то ей присваивается значение i1, т.е. i:=i1).
2. Выполнение действий, предусмотренных в теле цикла.
3. Изменение параметра цикла, который обеспечивает вычисление результата с новыми начальными данными (например, если параметр цикла i изменяется с шагом i3, i:=i+ i3) и переход к следующему шагу.
4. Проверка текущего значения параметра цикла с заданным конечным значением (i
Алгоритмические структуры
Любой алгоритм можно построить из ограниченного числа структурных конструкций. Обычно выделяют три структуры: линейную, разветвленную и циклическую.
Линейной структурой или следованием называют последовательное однократное выполнение двух или более операторов. Например:
Разветвленная структура предусматривает выбор одной из двух или более последовательностей операторов в зависимости от некоторого условия. Основной вариант реализации в программе — с помощью условного оператора:
Если значение логического выражения — истина, выполняется «оператор1», иначе (т.е. при ложности логического выражения) — «оператор2».
Пример:
При положительном x переменная y получит значение квадратного корня из x, в другом случае — значение 0.
Если нужно выбирать более чем из 2 вариантов, используют вложенные условные операторы, например:
Второй вариант реализации ветвления — оператор множественного выбора:
Оператор выбора используется только в тех случаях, когда «ключевое» выражение может принимать несколько конкретных значений. В программе указывается действия, выполняемые при каждом из этих значений. В ряде реализаций языка может быть также указан оператор, выполняемый при несовпадении выражения ни с одним из перечисленных значений (эта часть, начинающаяся вместо значения словом «otherwise» или, в зависимости от реализации, «else», всегда записывается последней).
Пример:
В алгоритме циклической структуры некоторая последовательность действий повторяется многократно. Последовательность операторов, описывающих повторяющиеся действия, называют телом цикла.
В программе циклическая структура реализуется с помощью операторов цикла. В Pascal имеется 3 типа таких операторов: цикл с предусловием, цикл с постусловием и цикл с параметром. Они отличаются друг от друга тем, как определяется число повторений.
Циклы с условием обычно используются в тех случаях, когда число повторений заранее неизвестно. Нужно повторять действия еще раз либо цикл должен быть завершен, определяется условием.
Если условие проверяется перед выполнением действий тела цикла, то такой цикл называют циклом с предусловием или циклом «пока» («повторять пока истинно условие»). В Pascal он выглядит следующим образом:
Пример:
Такая запись обозначает: пока значение переменной a превосходит 10, из него следует извлекать квадратный корень. Предположим, что до начала цикла переменная имела значение 10000. Поскольку 10000 > 10, из него будет извлечен корень; переменная получит значение 100. С этим значением вновь проверяется условие повторения. 100 больше 10, поэтому квадратный корень извлекается еще раз; переменная получает значение 10. Опять проверяется условие, но на этот раз 10 не больше 10, значит цикл будет завершен, и компьютер перейдет к исполнению следующего оператора.
Другой тип цикла с условием — цикл с постусловием, в котором проверка условия происходит после выполнения операторов тела цикла. Действия повторяются до того момента, когда условие станет истинным. В Pascal он записывается следующим образом:
Пример:
Этот фрагмент программы осуществляет ввод исходных данных с проверкой их корректности. Запрос будет повторяться до тех пор, пока пользователь не введет значение, удовлетворяющее поставлеенному условию (в данном случае — положительное).
В тех случаях, когда количество посторений известно заранее (до начала цикла), обычно бывает удобнее использовать цикл с параметром. Он выполняется следующим образом: переменная-параметр (её также называют счетчиком) принимает последовательные значения в заданных пределах и при каждом из них выполняются операторы тела цикла.
В Pascal оператор цикла с параметром выглядит следующим образом:
(в таком случае параметр будет увеличиваться). Если необходимо, чтобы значения параметра убывали, оператор немного изменяется:
Пример 1:
При выполнении этого фрагмента программы переменная i примет поочередно все значения от 1 до 20, при каждом из них на экран на отдельной строке (writeln) будет выводиться само это значение и его куб. В результате получится таблица кубов первых двадцати натуральных чисел. Чтобы значения выводились ровными колонками, в процедуре вывода указан формат (на значение переменной i отведено 3 позиции, для куба — 5).
Пример 2:
Этот фрагмент программы выведет на экран английский алфавит в обратном порядке —от «z» до «a»:
Информатика. 11 класс
Конспект урока
Информатика, 11 класс. Урок № 2.
Тема — Базовые алгоритмические структуры
Перечень вопросов, рассматриваемых в теме: алгоритм, блок-схема, следование, линейный алгоритм, ветвление, полная форма ветвления, неполная форма ветвления, разветвляющийся алгоритм, повторение, циклический алгоритм, цикл с предусловием, цикл с постусловием, цикл с параметром, комбинации базовых алгоритмических структур
Глоссарий по теме: следование, ветвление, повторение, цикл с предусловием, цикл с постусловием, цикл с параметром.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 11 класса
— М.: БИНОМ. Лаборатория знаний, 2017
Дополнительная литература по теме урока:
И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. Информатика и ИКТ. Профильный уровень: учебник для 11 класса — М.: БИНОМ. Лаборатория знаний, 2012
Теоретический материал для самостоятельного изучения
В 1969 году нидерландский ученый Эдсгер Дийкстра доказал важную теорему. Суть ее в том, что для решения любой логической задачи можно составить алгоритм, используя лишь три алгоритмических структуры: следование, ветвление и повторение. Эти структуры называют базовыми.
Самой простой структурой является «следование».
Алгоритм реализован через последовательную алгоритмическую структуру, если все команды этого алгоритма выполняются один раз, причем в том порядке, в котором они записаны.
Алгоритм, основанный на конструкции «следование» называется линейным алгоритмом. Примером такого алгоритма может служить алгоритм вычисления дискриминанта квадратного уравнения, блок-схема которого приведена на рисунке 1.
Следующей конструкцией является «ветвление». Она встречается, если действия алгоритма зависят от некоторого условия.
Алгоритм реализован через алгоритмическую конструкцию «ветвление», если от входных данных зависит, какие команды будут выполняться. Условие, которое выражает эту зависимость, фактически является вопросом, на который можно ответить либо «да», либо «нет».
Существуют полная и неполная формы ветвления.
В полной форме если условие выполняется, то алгоритм переходит к выполнению первой серии команд, а если не выполняется — то ко второй.
В неполной форме алгоритм выполняет серию команд только если условие истинно. В противном случае ничего не происходит.
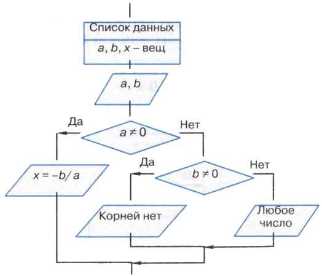
Алгоритм, основанный на конструкции «ветвление» называется разветвляющимся алгоритмом. Примером такого алгоритма может служить алгоритм нахождения корней квадратного уравнения, блок-схема которого приведена на рисунке 2.
И, наконец, последняя алгоритмическая конструкция — «повторение».
Алгоритм реализован с использованием алгоритмической конструкции «повторение», если некая группа подряд идущих шагов алгоритма (она называется телом цикла) может выполняться многократно в зависимости от входных данных.
Алгоритм, содержащий конструкцию «повторение» называется циклическим алгоритмом.
Существует несколько разновидностей циклических алгоритмов.
Первый — цикл с заданным условием продолжения работы (цикл с предусловием или цикл-пока).
Второй — цикл с заданным условием окончания работы (цикл с постусловием или цикл-до).
И третий — цикл с заданным числом повторений (цикл с параметром).
Доказано, что при решении задач можно ограничиться только одним циклом — циклом с предусловием. Но в ряде случаев цикл с постусловием или цикл с параметром делают решение задачи легче.
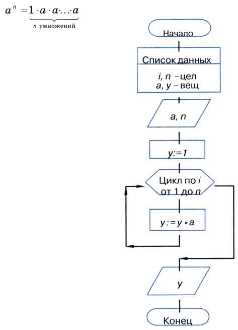
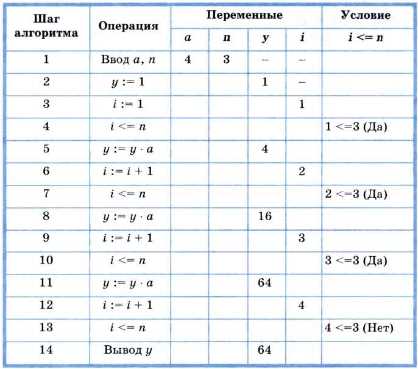
Примером решения одной и той же задачи с помощью различных циклов может служить задача возведения некоторого числа a в натуральную степень n.
Ключевые слова:
• следование
• ветвление
• повторение
• линейные алгоритмы
• разветвляющиеся алгоритмы
• циклические алгоритмы
Человеку в жизни приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.
2.4.1. Следование
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Графическое представление алгоритмической конструкции «следование» приведено на рис. 2.8.
Рис. 2.8. Алгоритмическая конструкция «следование»
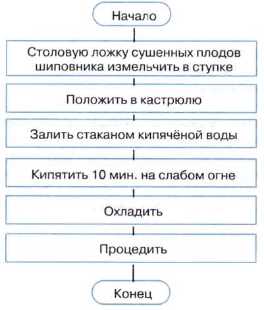
Пример 1. Линейный алгоритм приготовления отвара шиповника.
Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний.
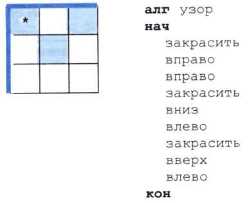
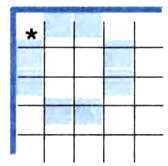
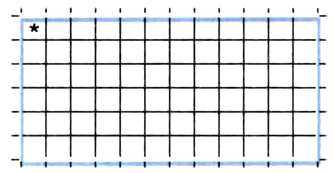
Пример 2. У исполнителя Робот есть четыре команды перемещения ( вверх, вниз, влево и вправо ), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение, обозначенное звёздочкой:
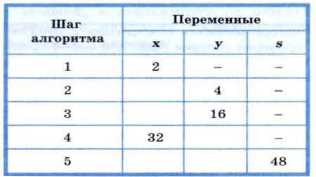
Пример 3. Дан фрагмент линейного алгоритма:
Выясним, какое значение получит переменная s после выполнения этого фрагмента алгоритма. Для этого составим таблицу значений переменных, задействованных в алгоритме:
Составленная нами таблица значений переменных моделирует работу исполнителя этого алгоритма.
Пример 4. Некоторый исполнитель может выполнять над целыми числами кроме операций сложения, вычитания, умножения и деления ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.
Например: 5 div 2 = 2; 5 mod 2 = 1; 2 div 5 = 0; 2 mod 5 = 2.
Покажем, как с помощью этих операций можно реализовать алгоритм работы кассира, выдающего покупателю сдачу (s) наименьшим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10) рублей.
Исполните алгоритм для s = 745 и s = 1864. Составьте соответствующие таблицы значений переменных.
Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
2.4.2. Ветвление
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Блок-схема ветвления представлена на рис. 2.9. Каждая ветвь может быть любой степени сложности (рис. 2.9, а), а может вообще не содержать предписаний (рис. 2.9, б).
Рис. 2.9. Структура «ветвление»: а — полная форма ветвления; б — неполная форма ветвления
На алгоритмическом языке команда ветвления записывается так:
Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:
А В — А больше В;
А>=В — А больше или равно В;
А<>B — А не равно В.
Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.
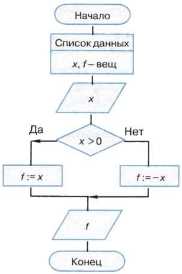
Пример 7. Алгоритм вычисления функции f(x) = |x| для произвольного числа х.
Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.
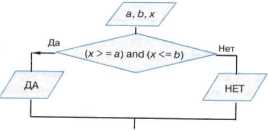
Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.
Пример 8. Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.
Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.
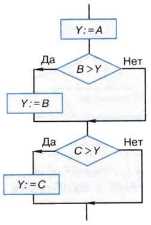
Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, В и С.
Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:
Пример 10. Алгоритм решения линейного уравнения ax + b = 0.
Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:
Также Робот может действовать в зависимости от выполнения составных условий.
Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Алгоритмы с ветвящейся структурой» (217044). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
2.4.3. Повторение
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.
В зависимости от способа организации повторений различают три типа циклов:
1) цикл с заданным условием продолжения работы;
2) цикл с заданным условием окончания работы;
3) цикл с заданным числом повторений.
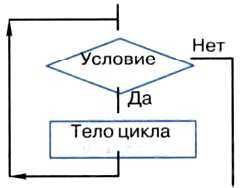
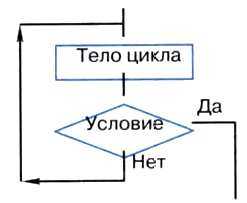
Цикл с заданным условием продолжения работы (цикл-ПОКА, цикл с предусловием). Логика работы этой конструкции описывается схемой, показанной на рис. 2.10.
Рис. 2.10. Цикл с предусловием
На алгоритмическом языке эта конструкция записывается так:
Выполняется цикл-ПОКА следующим образом: 1) проверяется условие (вычисляется значение логического выражения); 2) если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу.
Пример 12. Алгоритм, по которому из всех имеющихся кирпичей отбираются целые кирпичи и складываются в машину.
Пример 13. Правее Робота (клетка со звёздочкой) расположен коридор неизвестной длины. Необходимо, чтобы Робот закрасил все клетки этого коридора.
Пока будет выполняться условие справа свободно, Роботу следует выполнять команды:
Соответствующий алгоритм для Робота будет иметь вид:
нц пока справа свободно
вправо
закрась
кц
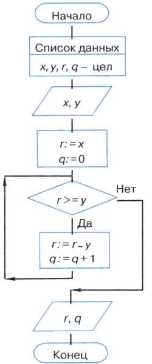
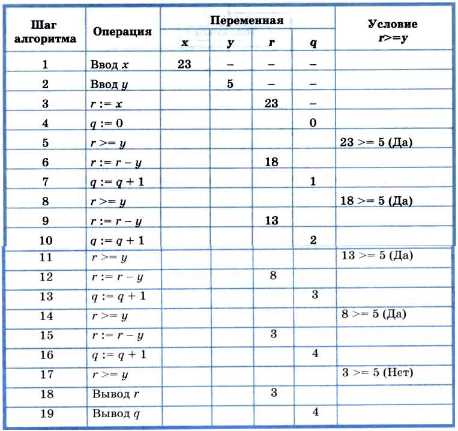
Пример 14. Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления натурального числа х на натуральное число у.
Представим операцию деления как последовательные вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет равно частному от деления q, а последняя разность — остатку от деления r.
Исполним этот алгоритм для х = 23 и у = 5.
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с предусловием» (217033). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием). Логика работы этой конструкции описывается схемой, показанной на рис. 2.11.
Рис. 2.11. Цикл с постусловием
На алгоритмическом языке эта конструкция записывается так:
нц
кц при
Выполняется цикл-ДО следующим образом: 1) выполняется тело цикла; 2) проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется («Нет»), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз.
Пример 15. Алгоритм по выучиванию наизусть четверостишия, алг четверостишие нач нц прочитать четверостишие по книге 1 раз рассказать четверостишие кц при не сделал ошибку кои
Пример 16. Вычислим значение переменной b согласно следующему алгоритму:
Составим таблицу значений переменных, задействованных в алгоритме:
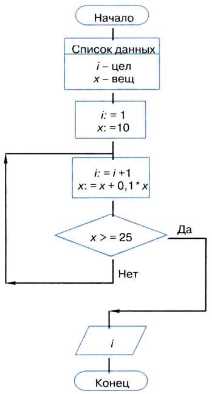
Пример 17. Спортсмен приступает к тренировкам по следующему графику: в первый день он должен пробежать 10 км; каждый следующий день следует увеличивать дистанцию на 10% от нормы предыдущего дня. Как только дневная норма достигнет или превысит 25 км, необходимо прекратить её увеличение и далее пробегать ежедневно ровно 25 км. Начиная с какого дня спортсмен будет пробегать 25 км?
Пусть х — количество километров, которое спортсмен пробежит в некоторый i-й день. Тогда в следующий (i + 1)-й день он пробежит х + 0,1x: километров (0,1x — это 10% от х).
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с постусловием» (217037). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
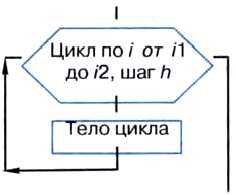
Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром). Логика работы этой конструкции описывается схемой, показанной на рис. 2.12.
Рис. 2.12. Цикл с параметром
На алгоритмическом языке эта конструкция записывается так:
нц для i от i1 до i2 шаг R
кц
В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения i1 до конечного значения i2 с шагом R.
Выполняется цикл-ДЛЯ следующим образом: 1) параметру цикла присваивается начальное значение; 2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.
Если величина шага в цикле с параметром равна единице, то шаг не указывают. Мы ограничимся рассмотрением именно таких циклов.
В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.
Пример 18. Алгоритм переправы через реку воинского отряда из пяти человек. Солдаты могут воспользоваться помощью двух мальчиков — хозяев небольшой лодки, в которой может переправиться или один солдат, или два мальчика.
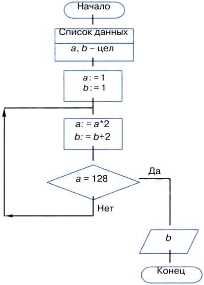
Пример 19. Составим алгоритм вычисления степени с натуральным показателем п для любого вещественного числа а.
При составлении алгоритма воспользуемся единой формулой, в которой число умножений равно показателю степени:
Исполним этот алгоритм для a = 4 и n = 3.
Пример 20. Для исполнителя Робот цикл с известным числом повторений реализуется с помощью следующей конструкции:
нц pas
кц
Так, если правее Робота не встретится препятствий, то, выполнив приведённый ниже алгоритм, он переместится на пять клеток вправо и закрасит эти клетки:
Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с параметром» (217024). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
САМОЕ ГЛАВНОЕ
Для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения.
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными.
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию «повторение», называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла. В зависимости от способа организации повторений различают три типа циклов:
1) цикл с заданным условием продолжения работы;
2) цикл с заданным условием окончания работы;
3) цикл с заданным числом повторений.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Какие алгоритмы называются линейными?
3. Приведите пример линейного алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
4. Запишите линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение:
5. По алгоритму восстановите формулу.
6. Какое значение получит переменная у после выполнения алгоритма?
Восстановите формулу вычисления у для произвольного значения X.
7. Для заданного количества суток (tƒh) требуется определить количество часов (h), минут (m) и секунд (с).
8. Известно, что 1 миля = 7 вёрст, 1 верста = 500 саженей, 1 сажень = 3 аршина, 1 аршин = 28 дюймов, 1 дюйм = 25,4 мм. Пользуясь этой информацией, составьте линейный алгоритм перевода расстояния X миль в километры.
9. Исходное данное — целое трёхзначное число х. Выполните для х = 125 следующий алгоритм.
а:=х div 100
b:=x mod 100 div 10
с: =х mod 10
s:=a+b+c
Какой смысл имеет результат s этого алгоритма?
10. Определите значение целочисленных переменных x и y после выполнения алгоритма.
11. Какие алгоритмы называют разветвляющимися?
12. Приведите пример разветвляющегося алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
13. Дополните алгоритм из примера 9 так, чтобы с его помощью можно было найти наибольшую из четырёх величин А, В, С и D.
14. Составьте алгоритм, с помощью которого можно определить, существует ли треугольник с длинами сторон а, b, с.
15. Составьте алгоритм, с помощью которого можно определить, является ли треугольник с заданными длинами сторон а, b, с равносторонним.
16. Составьте алгоритм возведения чётного числа в квадрат, а нечётного — в куб.
17. Какая задача решается с помощью следующего алгоритма?
18. Составьте блок-схему алгоритма определения количества чётных чисел среди заданных целых чисел А, Б и С.
19. Составьте блок-схему алгоритма определения принадлежности точки X отрезку [А, B] (пример 8) с использованием комбинации из двух ветвлений.
20. Составьте блок-схему алгоритма правописания приставок, оканчивающихся на букву «з».
21. Известно, что 31 января 2011 года было понедельником. Какие значения должны быть присвоены литерной переменной у в алгоритме, определяющем день недели для произвольного числа (chislo) января 2011 года?
22. Даны две точки на плоскости. Определите, какая из них находится ближе к началу координат.
23. Определите, есть ли среди цифр заданного целого трёхзначного числа одинаковые.
24. Приведите пример циклического алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
25. Напишите алгоритм, под управлением которого Робот обойдёт прямоугольную область, обнесённую стеной, по периметру и закрасит угловые клетки. Размеры области неизвестны.
26. Запас рыбы в пруду оценён в А тонн. Ежегодный прирост рыбы составляет 15%. Ежегодный план отлова — В тонн. Наименьший запас рыбы составляет С тонн. (Запас ниже С тонн уже не восстанавливается.) Составьте блок-схему алгоритма для подсчёта количества лет, в течение которых можно выдерживать заданный план.
28. Составьте алгоритм для определения количества цифр в записи произвольного натурального числа.
29. Сумма 10 000 рублей положена в сберегательный банк, при этом прирост составляет 5% годовых. Составьте алгоритм, определяющий, через какой промежуток времени первоначальная сумма увеличится в два раза.
30. Одноклеточная амёба каждые три часа делится на 2 клетки. Составьте алгоритм вычисления времени, через которое будет X амёб.
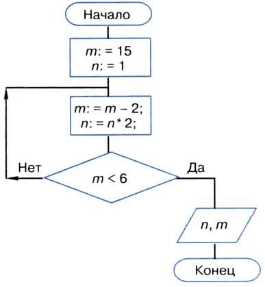
31. Определите значения переменных n и m после выполнения алгоритма.
32. Составьте алгоритм нахождения произведения z двух натуральных чисел х и у без использования операции умножения.
33. Население города Н увеличивается на 5% ежегодно. В текущем году оно составляет 40 000 человек. Составьте блок-схему алгоритма вычисления предполагаемой численности населения города через 3 года. Составьте таблицу значений переменных, задействованных в алгоритме.
34. Каждая бактерия делится на две в течение 1 минуты. В начальный момент имеется одна бактерия. Составьте блок-схему алгоритма вычисления количества бактерий через 10 минут. Исполните алгоритм, фиксируя каждый его шаг в таблице значений переменных.
Электронное приложение к уроку
 |  |  |
| Файлы | Материалы урока | Ресурсы ЭОР |
Cкачать материалы урока