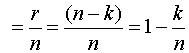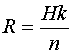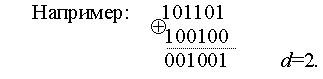какими помехозащитными свойствами обладают циклические коды

Электронные средства сбора, обработки и отображения информации

Оглавление

Помехоустойчивое кодирование

Понятие корректирующего кода

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.

Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).

В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.

Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.

Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.

Различают разделимые и неразделимые блоковые коды.

При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.

При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Общие принципы использования избыточности

Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть различных входных последовательностей и различных выходных последовательностей. Из общего числа выходных последовательностей только последовательностей соответствуют входным. Будем называть их разрешенными кодовыми комбинациями. Остальные ( — ) возможных выходных последовательностей для передачи не используются. Их будем называть запрещенными кодовыми комбинациями.

— случаев безошибочной передачи;

— ·(-1) случаев перевода в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам;

— ·( — ) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.

Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:

К_обн .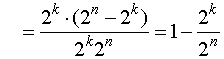

Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит , то есть вдвое больше общего числа кодируемых входных последовательностей. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество комбинаций, содержащих четное число единиц (или нулей). При кодировании к каждой последовательности из k информационных символов добавляется один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Искажение любого четного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть обнаруженных ошибок составляет:

К_обн .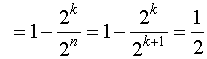

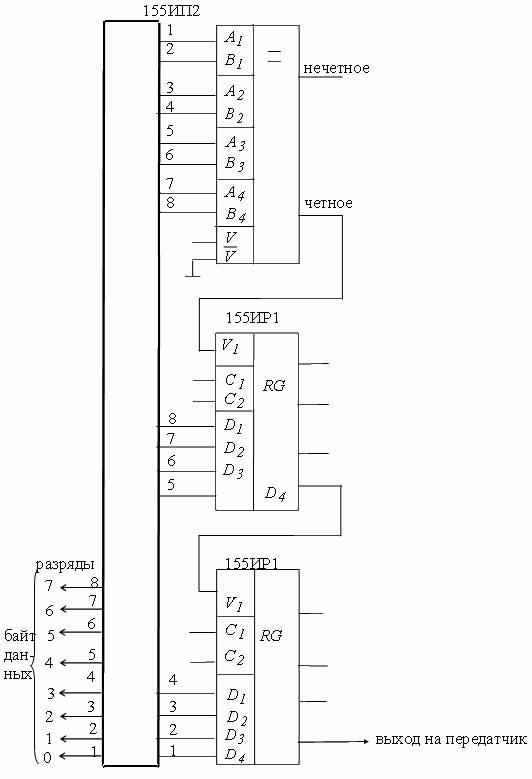
Пример кодирующего устройства с проверкой на четность показан на рис.

Основные параметры корректирующих кодов

Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.

Рассмотрим суть этих параметров.

Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов

Относительной избыточностью корректирующего кода называют величину

_отн

_отн.

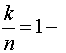
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.

Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна

поскольку в последовательности из п символов только k информационных.

Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.

Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.

Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.

Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.

Число обнаруживаемых ошибок определяется минимальным расстоянием между кодовыми комбинациями. Это расстояние называется хэмминговым.

В безызбыточном коде все комбинации являются разрешенными, =1. Достаточно только исказиться одному символу, и будет ошибка в сообщении.

Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.

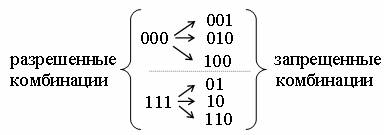
Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как =1. Если =2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию.

Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:

Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности — минимальное хэммингово расстояние должно быть, по крайней мере, на единицу больше , то есть

+1.

В этом случае никакая ошибка кратности не в состоянии перевести одну разрешенную комбинацию в другую.

Ошибки можно не только обнаруживать, но и исправлять.

Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.

Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.

Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:

В общем случае исправляемые ошибки кратности связаны с кодовым расстоянием соотношением

=2+1. (2.1)

где — сочетание из п элементов по t (число возможных ошибок кратности t на длине п-разрядной комбинации).

Если, например, п=7, =1, то из (2.1)

Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.

Групповой код с проверкой на четность

Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:

Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы . Контрольные символы образуются путем суммирования по модулю 2 информационных символов, расположенных в столбце:

.

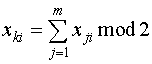
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.

Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).

Если проверка проводится по строкам и столбцам, то код называется матричным.

Проверочные символы располагаются следующим образом:

;

.

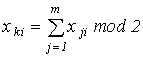
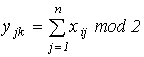
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.

Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.

Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.

Коды с постоянным весом

Весом называется число единиц, содержащихся в кодовых комбинациях.

В коде «3 из 7» возможных комбинаций сто двадцать восемь (=128), а разрешенных кода только тридцать пять. Относительная избыточность _отн = 0,28.

Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.

Циклические коды

Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.

— комбинация циклического кода;

— также комбинация циклического кода.

Например, комбинация 1001111 (п=7) будет представлена многочленом

При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.

Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.

Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:

Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.

Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=+1. При таком формировании кодовых комбинаций позиции информационных и контрольных символов заранее определить нельзя.

Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.

Число разрядов регистра выбирается равным степени образующего полинома.

Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.

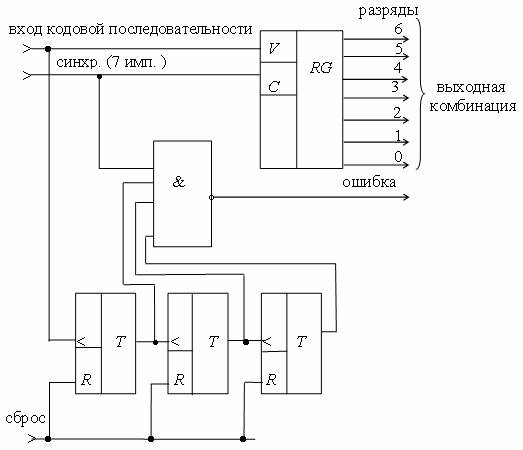
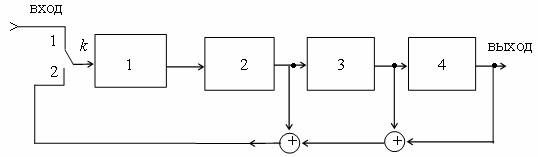
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.

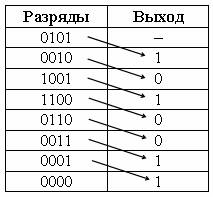
В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.

Свойства циклического кода:

1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;

2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;

Источник

Помехоустойчивое кодирование с иcпользованием различных кодов

Это продолженеие статьи о помехоустойчивом кодировании, которая очень долго лежала в черновиках. В прошлой части нет ничего интересного с практической точки зрения — лишь общие сведения о том, зачем это нужно, где применяется и т.п. В данной части будут рассматриваться некоторые (самые простые) коды для обнаружения и/или исправления ошибок. Итак, поехали.

Попытался все описать как можно легче для человека, который никогда не занимался кодированием информации, и без каких-либо особых математических формул.

Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.

По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Избыточность кода — это количество проверочной информации в сообщении. Рассчитывается она по формуле:

k/(i+k), где
k — количество проверочных бит,
i — количество информационных бит.

Например, мы передаем 3 бита и к ним добавляем 1 проверочный бит — избыточность составит 1/(3+1) = 1/4 (25%).

Код с проверкой на четность

Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.

Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.

Код Хэмминга

первый проверочный бит на 2 0 = 1;
второй проверочный бит на 2 1 = 2;
третий проверочный бит на 2 2 = 4;

r1 = i1 + i2 + i4
r2 = i1 + i3 + i4
r3 = i2 + i3 + i4

В принципе, работа этого алгоритма разобрана очень детально в статье Код Хэмминга. Пример работы алгоритма, так что особо подробно описывать в этой статье не вижу смысла. Вместо этого приведу структурную схему кодера:

и декодера

(может быть, довольно запутано, но лучше начертить не получилось)

e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:

e0 = k1 + k3 + k5 + k7 mod 2
e1 = k2 + k3 + k6 + k7 mod 2
e2 = k4 + k5 + k6 + k7 mod 2

Набор этих значений e2e1e0 есть двоичная запись позиции, где произошла ошибка при передаче данных. Декодер эти значения вычисляет, и если они все не равны 0 (то есть не получится 000), то исправляет ошибку.

Коды-произведения

В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке:

Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке:

Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования. Здесь к ним добавляются проверочные символы, а они, в свою очередь, заносятся в буфер по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.

При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается куда-нибудь. Условимся, что и внутренний, и внешний коды – коды Хэмминга, с тремя проверочными символами, то есть и тот, и другой могут исправить по одной ошибке в кодовом слове (количество «кубиков» на рисунке не критично — это просто схема). На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (крестики на рисунке в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена.

Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце — две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.

Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.

Источник