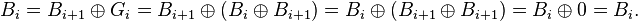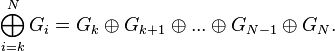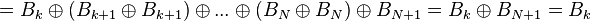код грея перевод в двоичный код
Код ГРЕЯ в многопозиционных видах модуляций
При многопозиционных видах модуляций (М-ФМн и М-КАМ) выбор положения символа в сигнальном созвездии влияет на вероятность битовой ошибки.
Рассмотрим положение символов в сигнальном созвездии для четверичной фазовой модуляции. Для 4-ФМн каждый символ представляется 2 битами. Назначим каждому символу по часовой стрелке комбинацию бит в обычной двоичной системе счисления: <00; 01; 10; 11>.
При воздействии шумов могут возникать ошибки, которые появляются в результате того, что был принят не тот символ, который передавался. Вероятность перепутать один символ с другим (т.е. допустить ошибку при приёме) тем больше, чем ближе символы на созвездии находятся друг к другу.
Пример кодирования двоичного кода
Рассмотрим пример по рисунку выше. Пусть был передан символ S0, который кодирован битами <00>. Из-за воздействия шумов наиболее частой ошибкой будет прием символа S1 или S3, т.к. они расположены ближе, чем символ S2. Ошибочный прием символа S2 также будет, но такие ошибки будут происходить реже.
Если возникла ошибка, при которой был принят символ S1 <01>вместо S0 <00>, то будет потерян всего 1 бит информации, т.к. символ S1 отличается от символа S2 на один бит. Однако если возникла ошибка, при которой был принят символ S3 <11>, то будет потеряно уже 2 бита информации.
Возникает вопрос, можно ли символам назначить такие комбинации бит, чтобы любые два соседних символа отличались не более чем на один бит. Ответ на этот вопрос положительный – нужно воспользоваться кодом Грея.
Код Грея определение
В таблице ниже представлен код Грея для 2-х и 3-х бит.
Код Грея образуется путем перестановки некоторых кодовых комбинаций таким образом, что любые две соседние кодовые комбинации отличаются друг от друга на один бит.
Если символы 4-ФМн закодировать кодом Грея, т.е. символам S0 S1 S2 S3 назначить комбинацию бит <00; 01; 10; 11>соответственно, то любые два соседних символа будут отличаться друг от друга не более чем на один бит. В этом случае, если произойдет любая ошибка, где будут перепутаны два соседних символа, будет потерян только один бит информации.
Код Грея применим в том случае, когда у каждого символа в созвездии только два соседа, т.е. близлежащих символов. Это случай четверичной и восьмеричной фазовой манипуляции.
Если рассматривать созвездие амплитудно-фазовых модуляций, в том числе КАМ, то видно, что у каждого символа более двух соседей. В этом случае нельзя придумать такой код, при котором все близлежащие символы отличались бы только на один бит. Но и в этом случае играет большую роль, каким символам, какие кодовые комбинации назначаются. Те символы, которые расположены ближе всего друг к другу, должны отличаться на минимальное количество бит, в идеальном случае на один.
Если невозможно сделать так, чтобы все соседи отличались на один бит, тогда допускается отличие на два бита, и т.д. Чем дальше символы в созвездии располагаются друг от друга, тем реже возникает ошибка, при которой эти символы будут перепутаны, следовательно, тем на большее количество бит они могут отличаться.
Задача назначения битовых комбинаций каждому символу в созвездии сводится к минимизации среднего количества битовых ошибок при фиксированном отношении сигнал/шум.
Язык описания аппаратуры Verilog HDL
Как мы знаем, коды Грея (Gray codes) – это специальная система счисления, в которой два соседних значения отличаются только в одном разряде. Они часто используются для повышения надежности аппаратуры. Одно из применений кодов Грея – передача значений указателей головы/хвоста очереди из одного клокового домена в другой при проектировании асинхронного FIFO.
Рассмотрим способы преобразования кодов Грея в двоичное число.
Вот таблица соответствия для четырехбитных чисел:
0000 0000
0001 0001
0010 0011
0011 0010
0100 0110
0101 0111
0110 0101
0111 0100
1000 1100
1001 1101
1010 1111
1011 1110
1100 1010
1101 1011
1110 1001
1111 1000
Столбец слева – это двоичное число, а столбец справа – это соответствующие коды Грея.
Преобразование из Грея в двоичное число можно сделать на языке Verilog HDL вот так:
module gray2bin_v1(
input wire [3:0]gray,
output wire [3:0]bin
);
assign bin[0] = gray[3] ^ gray[2] ^ gray[1] ^ gray[0];
assign bin[1] = gray[3] ^ gray[2] ^ gray[1];
assign bin[2] = gray[3] ^ gray[2];
assign bin[3] = gray[3];
endmodule Используются только операции «Исключающее ИЛИ». Если откомпилировать такой модуль с помощью Quartus II, то в его RTLViewer можно увидеть получившуюся эквивалентную схему:
Для проверки правильности работы этого модуля напишем Verilog тестбенч: ` timescale 1ns/1ns
reg clk;
initial clk=0;
always
#10 clk=
reg [3:0]gr;
wire [3:0]b1;
gray2bin_v1 my_gr1(
.gray(gr),
.bin(b1)
);
initial
begin
$dumpfile(«out.vcd»);
$dumpvars(-1, test);
gr=4’b0000;
@( posedge clk); #0;
@( posedge clk); #0;
gr=4’b0001;
@( posedge clk); #0;
gr=4’b0011;
@( posedge clk); #0;
gr=4’b0010;
@( posedge clk); #0;
gr=4’b0110;
@( posedge clk); #0;
gr=4’b0111;
@( posedge clk); #0;
gr=4’b0101;
@( posedge clk); #0;
gr=4’b0100;
@( posedge clk); #0;
gr=4’b1100;
@( posedge clk); #0;
gr=4’b1101;
@( posedge clk); #0;
gr=4’b1111;
@( posedge clk); #0;
gr=4’b1110;
@( posedge clk); #0;
gr=4’b1010;
@( posedge clk); #0;
gr=4’b1011;
@( posedge clk); #0;
gr=4’b1001;
@( posedge clk); #0;
gr=4’b1000;
@( posedge clk); #0;
$finish();
end
endmodule Быстро просимулировать и посмотреть результат можно с помощью iverilog (Icarus Verilog), используя командную строку и GtkWave. Здесь же я приведу лишь получившуюся временную диаграмму:
Все работает правильно.
Недостаток описанного выше примера модуля gray2bin_v1 состоит в том, что он реализует фиксированное число бит, в данном случае четыре. Было бы удобным иметь параметризованный модуль, который без изменений мог бы быть использованным в разных проектах.
Если внимательно посмотреть на код модуля gray2bin_v1, то видно, что там имеется четыре строки assign для каждого результирующего бита. Нам нужен механизм создания заданного числа таких строк кода Verilog в момент компиляции и такой механизм есть в стандарте Verilog-2001. Использование конструкции языка generate/endgenerate позволяет в момент компиляции генерировать фрагменты кода.
Вот пример параметризованного модуля преобразователя кода Грея в двоичный код: module gray2bin_v2(
input wire [SIZE-1:0]gray,
output wire [SIZE-1:0]bin
);
parameter SIZE = 4;
Конечно, можно написать модуль gray2bin и иначе, без «экзотических» generate/endgenerate. Вот так: module gray2bin_v3(
input wire [SIZE-1:0]gray,
output reg [SIZE-1:0]bin
);
parameter SIZE = 4;
always @*
begin
for (i=0; i >i);
end
endmodule
Здесь, выражение (gray>>i) – это логический сдвиг вправо, он оставляет только нужные биты, между которыми будет проводиться «Исключающее ИЛИ». К сожалению, написать здеь gray[SIZE-1:i] вместо (gray>>i) не получится. Компилятор Verilog выдаст ошибку. Язык Verilog не позволяет выбрать часть бит из шины если один из индексов это переменная.
Модули gray2bin_v2 и gray2bin_v3 описывают одно и то же, разными способами. Они работают одинаково. В этом легко убедиться с помощью того же тестбенча, описанного выше.
Код грея перевод в двоичный код
Среди невзвешенных двоичных кодов специальные применения находят такие, у которых переход к соседнему числу сопровождается изменениями только в одном разряде (коды с обменной единицей). Так, в технике аналого-цифрового преобразования и пересчетных устройствах широко используется код Грея [73], называемый также циклическим или рефлексно-двоичным кодом (табл. 1.3). Он позволяет существенно сократить гремя преобразования, упростить кодирующую логику, а также повысить эффективность защиты от нежелательных сбоев при переходах выходного кода. Недостатком кода Грея является то, что в нем затруднено выполнение арифметических операций и цифроаналоговое преобразование. Поэтому при необходимости код Грея преобразуется в обычный двоичный код.
Переход от двоичного кода к коду Грея осуществляется по правилу (рис. 1.2,а): старшие разряды совпадают, а любой следующий разряд 

14. Код Грея



Эту процедуру можно также свести к последующему просмотру и преобразованию цифр кода Грея, начиная со старшего разряда: цифра остается без изменения, если число предшествующих единиц четно (иуль считается четным числом) и инвертируется, если число предшествующих единиц нечетно.
Счётчик Грэя
Автор: Белоусов Аркадий
Введение
Известно множество схем кодирования чисел (систем счисления) — совокупностей символов и правил их комбинации для обозначения числа. Основной признак, по которому все системы разделяют — позиционная ли это система. В свою очередь, позиционные системы различаются «весами», соответствующими каждой позиции в представлении числа. В одних системах вес цифры каждого разряда меньше веса цифры следующего старшего разряда в одно и тоже число раз. В других системах для каждого разряда определён свой вес, который может быть равен, больше или меньше весов других разрядов в произвольное число раз.
К позиционным системам с постоянным основанием относится десятичная система, системой с произвольным основанием является система счёта времени — секунд в минутах и минут в часах по 60, а часов в сутках 24. Непозиционные системы счисления из повседневности практически вытеснены, хотя римская система до сих пор используется, например, для указания номера века, а иногда и года.
В современных цифровых компьютерах основное место занимает двоичная система счисления (позиционная система с постоянным основанием, равным 2) и прямые её производные (восьмеричная и шестнадцатиричная системы). Однако и другие системы не были забыты. Например, при двоично-десятичном кодировании чисел каждой десятичной цифре отводится по четыре двоичных цифры (бита), веса которых могут быть равны не только 8-4-2-1, но и, скажем, 2-4-2-1.
Встречаются в цифровой технике и непозиционные системы. Наиболее известныйиз них — код Грея, называемый также рефлексным (отражённым) двоичным кодом. Этот код строится из двоичных цифр таким образом, что соседние числа в нём отличаются всегда только в одном разряде. Кодов с такой же характеристикой много, но для кода Грея имеется простой алгоритм перевода чисел в двоичный позиционный код и обратно.
Строение кода Грея
Код Грея — непозиционный код с одним набором символов (0 и 1) для каждого разряда. Таким образом, в отличие от римской системы счисления число в коде Грея не является суммой цифр. Чтобы показать соответствие последовательности чисел коду Грея можно воспользоваться таблицей, но есть и наглядное правило построения этой последовательности.
Младший разряд в последовательности чисел в коде Грея принимает значения 0 и 1, затем следующий старший разряд становится единичным и младший разряд принимает свои значения уже в обратном порядке (1, 0). Этим и объясняется название кода — «отражённый». Соответственно, два младших разряда принимают значения 00, 01, 11, 10, а затем, при единичном следующем старшем разряде, те же значения в обратном порядке (10, 11, 01, 00). Ниже дана таблица, показывающая первые восемь чисел в двоичном коде и в коде Грея.
| N | двоичный код | код Грея | N | двоичный код | код Грея |
| 0 | 000 | 000 | 4 | 100 | 110 |
| 1 | 001 | 001 | 5 | 101 | 111 |
| 2 | 010 | 011 | 6 | 110 | 101 |
| 3 | 011 | 010 | 7 | 111 | 100 |
Использование кода Грея
Благодаря своему основному свойству (отличие соседних чисел только в одном разряде) код Грея применяется, например, в построенных на кодовых дисках определителях углового положения вала. В оптическом кодовом диске единицы и нули кодируются прозрачными и непрозрачными областями. С одной стороны диск просвечивается ориентированной вдоль его радиуса световой щелью, с другой стороны размещаются фотодиоды. Считываемый с фотодиодов двоичный код и указывает угол поворота диска. Ниже показаны 3-разрядные диски на позиционном коде и коде Грея (в силу ограниченности выразительных средств диски «разрезаны» посредине последнего угла и «вытянуты» в ленту, как это делается и для карт земного шара):
| позиционный код |  |
| код Грея |  |
Недостаток кодирования позиционным двоичным кодом заключается в том, что при смене нечётного кода чётным считанный с фотодиода код может оказаться неверным. Характеристики фотодиодов обычно не идентичны и при смене сразу нескольких разрядов выходные уровни фотодиодов могут измениться не строго одновременно. Например, при переходе от третьего угла к четвёртому или от седьмого угла к нулевому меняются все разряды и какое-то время на выходе фотодиодов можно получить любое значение от 0 до 7.
В коде же Грея при переходах ошибка не будет превышать один угол.
Алгоритмы преобразования кода Грея
Как сказано выше, алгоритм перевода чисел в коде Грея в позиционный код прост: каждый разряд в позиционном коде равен сумме по модулю 2 этого и всех более старших разрядов в коде Грея. Старшие разряды, соответственно, совпадают. На языке C это алгоритм может выглядеть так:
unsigned gray2bin(unsigned v) < unsigned sum = v, length = BITS; while(length >0) v >>= 1, sum ^= v, length—; return sum; >
Этот код является дословным переводом на язык C основного алгоритма, но его можно оптимизировать за счёт накопления промежуточных сумм в самом числе:
for(unsigned i = 1; i > i);
Поскольку количество итераций здесь является уже логарифмом от числа бит и мало даже для очень больших чисел, то этот цикл лучше развернуть:
v ^= v >> 1; /* для 2-разрядных чисел */ v ^= v >> 2; /* для 4-разрядных чисел */ v ^= v >> 4; /* для 8-разрядных чисел */ v ^= v >> 8; /* для 16-разрядных чисел */ …
Перевод из позиционного кода в код Грея ещё проще: каждый разряд в коде Грея равен сумме по модулю 2 этого и следующего старшего разряда в позиционном коде. На языке C этот алгоритм реализуется выражением v^(v>>1). Реализации на языке C этих алгоритмов также представлены в отдельном файле [GRAY.C].
Заметьте: код Грея отличается от позиционного кода только интерпретацией значения бит в числе, поэтому числа в разных кодах можно хранить в одних и тех же переменных. Более того, одно и то же значение переменной также можно интерпретировать по-разному — это просто даст разные числа.
Литература
И.С.Потёмкин «Функциональные узлы цифровой автоматики», М.: Энергоатомиздат, 1988
ALGLIB® — numerical analysis library, 1999-2018.
ALGLIB is registered trademark of the ALGLIB Project.
Код грея перевод в двоичный код
Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивныйдвоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Содержание
[править] Название
Название рефлексный (отражённый) двоичный код происходит от факта, что вторая половина значений в коде Грея эквивалентна первой половине, только в обратном порядке, за исключением старшего бита, который просто инвертируется. Если же разделить каждую половину ещё раз пополам, свойство будет сохраняться для каждой из половин половины и т. д.
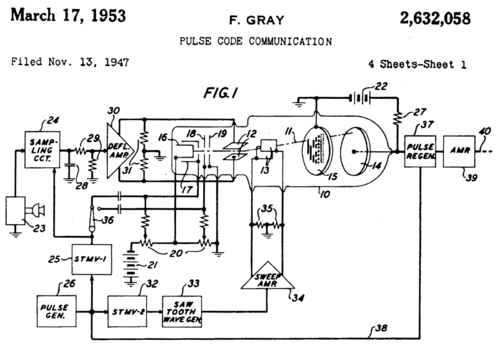
Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он запатентовал и использовал этот код в своей импульсной системе связи (патент № 2632058).
[править] Применения
Использование кодов Грея основано прежде всего на том, что он минимизирует эффект ошибок при преобразовании аналоговых сигналов в цифровые (например, во многих видах датчиков).
Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также они используются для кодирования номера дорожек в жёстких дисках.
Широко применяются коды Грея и в теории генетических алгоритмов [1] для кодирования генетических признаков, представленных целыми числами.
[править] Алгоритмы преобразования
[править] Преобразование двоичного кода в код Грея
Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит. Следовательно, i-й бит кода Грея G i выражается через биты двоичного кода B i следующим образом:
где 
Ниже приведён алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
Однако, необходимо помнить, что данный алгоритм будет работать правильно, если компилятор реализует циклический логический сдвиг (стандарт языка C не уточняет тип сдвига). Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать двоичное число 10110 в код Грея.
[править] Преобразование кода Грея в двоичный код
Обратный алгоритм – преобразование кода Грея в двоичный код – можно выразить рекуррентной формулой
причём преобразование осуществляется побитно, начиная со старших разрядов, и значение 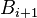
Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:
где N – число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак 
Действительно, подставив в формулу выражение для i-го бита кода Грея, получим

Здесь предполагается, что бит, выходящий за рамки разрядной сетки (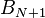
Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.
Тот же самый алгоритм, записанный на языке Паскаль:
Пример: преобразовать код Грея 11101 в двоичный код.
Быстрое преобразование 8/16/24/32-разрядного значения кода Грея в двоичный код на языке BlitzBasic:
Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».
[править] Генерация кодов Грея
Код Грея для n бит может быть рекурсивно построен на основе кода для n–1 бит путём переворачивания списка бит (то есть записыванием кодов в обратном порядке), конкатенации исходного и перевёрнутого списков, дописывания нулей в начало каждого кода в исходном списке и единиц — в начало кодов в перевёрнутом списке. Так, для генерации списка для n = 3 бит на основании кодов для двух бит необходимо выполнить следующие шаги:
| Коды для n = 2 бит: | 00, 01, 11, 10 | |
| Перевёрнутый список кодов: | 10, 11, 01, 00 | |
| Объединённый список: | 00, 01, 11, 10 | 10, 11, 01, 00 |
| К начальному списку дописаны нули: | 000, 001, 011, 010 | 10, 11, 01, 00 |
| К перевёрнутому списку дописаны единицы: | 000, 001, 011, 010 | 110, 111, 101, 100 |
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке Perl:
Рекурсивная функция построение кода Грея на языке C:
Быстрое преобразование 8/16/24/32-разрядного бинарного кода в код Грея на языке BlitzBasic: