код хемминга как решать
Избыточное кодирование, код Хэмминга
Избыточное кодирование (англ. redundant encoding) — вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.
| Определение: |
| Код определяет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования скажет, что есть ошибка. |
| Определение: |
| Код исправляет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования сможет восстановить исходное слово. |
Содержание
Код, определяющий одну ошибку [ править ]
Кодирование Хэмминга [ править ]
| [math]a[/math] | [math]b[/math] | [math]a \oplus b[/math] |
|---|---|---|
| [math]c[/math] | [math]d[/math] | [math]c \oplus d[/math] |
| [math]a \oplus c[/math] | [math] b \oplus d [/math] |
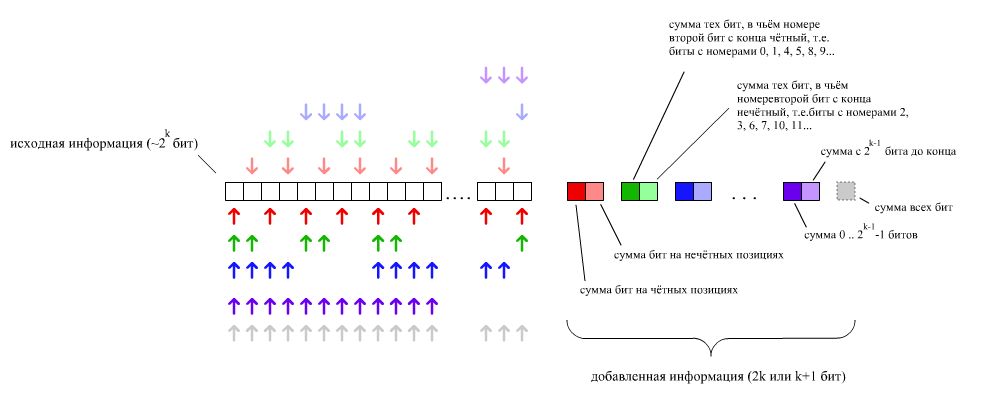
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в [math]2^k[/math] бит. Для получения её кода добавим к ней [math]k[/math] пар бит по следующему принципу:
Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит — [math] \mathrm X \mathrm O \mathrm R[/math] всех битов строки.
Определение и устранение ошибок в общем случае [ править ]
Пусть [math]\Sigma[/math] — исходный алфавит, [math]C: \Sigma \to B^m[/math] — кодирование, [math]B=(0,1)[/math]
[math]d: B^m \times B^m \to \mathbb
Определим [math]d_0 = \min[/math] [math]
Тогда легко понять, что код, полученный преобразованием [math]C[/math] может исправлять [math]
Light
ВНИМАНИЕ! Это разжёванная версия замечательной статьи, которая есть на хабре!
Если вам нужно лаконичное объяснение, то вам туда! Если же вы в этом ничего не понимаете и требуется пошаговое разбирательство, то милости прошу читать дальше. То есть, где вам понятнее — там и читайте. Статья на хабре не моя, но я считаю, что она шикарна!
Итак. Задача. Использовать код Хэмминга для двоичного сообщения, длина слова у которого составляет 16 бит. Исходное сообщение возьмём такое «0100010000111101». То есть в слове 16 «букв», каждая из которых может принимать значение либо «0», либо «1».
Кодирование
Сначала в исходное сообщение добавляем контрольные биты и устанавливаем их в нуль.
Контрольные биты располагаются в тех номерах битов, которые равны степеням двойки (ибо алфавит двоичный).
То есть. Два в степени нуль — это единица, два в степени 1 = два, два в степени 2 = четыре, а два в степени 3 = восемь, два в степени 4 = 16
Значит контрольные биты будут находиться в «буквах»(битах) под номерами 1, 2, 4, 8 и 16.
В остальные номера бит переписываем исходное сообщение.
Видно, что длина «слова» из-за такой избыточности увеличилась на пять «букв». В данном случае, конечно. У вас количество дополнительных бит будет зависеть от длины исходного «слова».
Теперь нужно вычислить эти контрольные биты.
Каждый контрольный бит с номером N «контролирует» непрерывную последовательность из N битов, через каждые N битов.
Вот на картинке отмечено иксами (X), какие биты нужно использовать для вычисления первого контрольного бита (с номером «1»)
Для вычисления контрольно бита нужно просто сложить все «буквы» нашего «слова», которые он контролирует, а затем принять нелёгкое решение: если сумма получилась чётная, то пишем в результате нуль, а если нечётная — единицу.
Вычисляем первый бит.
Складываем биты под номерами 3,5,7,9,11,13,15,17,19,21
Это будет 0 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 = 5
Получилось 5 (пять). Сумма нечётная (на два нацело не делится). Значит пишем в первый бит единицу:
Теперь вычислим контрольный бит номер 2. Для него нужно будет найти сумму каждых двух бит следующих друг за другом непрерывно, через каждые два бита. Такие биты я тоже отметил на картинке.
То есть будем теперь суммировать биты, начитая с третьего по номеру, и далее те, которые отмечены иксом (X).
Их номера 3, 6, 7, 10, 11, 14, 15, 18, 19.
Это будет 0 + 0 + 0 + 1 + 0 + 0 + 1 + 1 + 1 = 4
Четыре — число чётное, значит оставляем в нашем втором бите нуль.
Переходим к вычислению третьего контрольного бита. Но это у нас он контрольный — третий. А в сообщении этот бит записан под номером 4 — четыре.
Значит и использовать будем все попадающие под наше правило биты, начиная с пятого.
А это биты под номерами 5, 6, 7, 12, 13, 14, 15, 20, 21.
Складываем их: 1 + 0 + 0 + 0 + 0 + 0 + 1 + 0 + 1 = 3
В итоге у нас нечётное число, значит пишем в наш контрольный бит единицу.
Осталось всего ничего — вычислить два оставшихся контрольных бита, которые под номерами 8 и 16.
В восьмом оставляем нуль потому, что в той последовательности, которую мы используем для вычисления присутствуют две единицы, дающие в сумме чётное число.
А в 16-м тоже сумма бит получается чётной — оставляем нуль:
В итоге мы получили слово с кодом Хэмминга, которое содержит избыточные биты (в сумме 21): «100110000100001011101».
Декодирование
А теперь представим, что к нам пришло сообщение с ошибкой. Вот оно «100110001100001011101».
Мы знаем, что в него добавлены избыточные биты по алгоритму Хемминга, и нам надо проверить, есть в нём ошибка или нет.
Для этого нужно поступить следующим образом. Сначала вычисляем заново все контрольные биты по предыдущему алгоритму.
Для этого сначала обнуляем все биты, находящиеся на номерах степеней двойки:
В первом оставляем нуль, ибо в подконтрольных битах чётное число единиц.
Вычисляем все остальные контрольные биты по описанному выше алгоритму (мне лень заново его описывать тут), и получаем, что не совпадают контрольные биты под номерами 1 и 8:
Теперь складываем номера этих контрольных бит: 1 + 8, и получаем 9 — номер бита, в котором закралась ошибка! Ура! Теперь просто меняем девятый бит на обратный — с единицы на нуль, — и получаем исходное сообщение!
Отметим, что это самый простейший алгоритм Хемминга, который может исправить только одну ошибку в слове. Об остальных алгоритмах данная статья умалчивает. 🙂
Помехоустойчивое кодирование. Часть 1: код Хэмминга
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
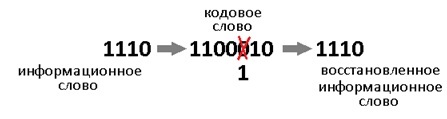
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Код хемминга как решать
Код Хэ́мминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построен применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную.
Предположим, что нужно сгенерировать код Хемминга для некоторого информационного кодового слова. В качестве примера возьмём 15-битовое кодовое слово x1…x15, хотя алгоритм пригоден для кодовых слов любой длины. В приведённой ниже таблице в первой строке даны номера позиций в кодовом слове, во второй — условное обозначение битов, в третьей — значения битов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Вставим в информационное слово контрольные биты r0…r4 таким образом, чтобы номера их позиций представляли собой целые степени двойки: 1, 2, 4, 8, 16… Получим 20-разрядное слово с 15 информационными и 5 контрольными битами. Первоначально контрольные биты устанавливаем равными нулю. На рисунке контрольные биты выделены розовым цветом.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
В общем случае количество контрольных бит в кодовом слове равно двоичному логарифму числа, на единицу большего, чем количество бит кодового слова (включая контрольные биты); логарифм округляется в большую сторону. Например, информационное слово длиной 1 бит требует двух контрольных разрядов, 2-, 3- или 4-битовое информационное слово — трёх, 5…11-битовое — четырёх, 12…26-битовое — пяти и т. д.
Добавим к таблице 5 строк (по количеству контрольных битов), в которые поместим матрицу преобразования. Каждая строка будет соответствовать одному контрольному биту (нулевой контрольный бит — верхняя строка, четвёртый — нижняя), каждый столбец — одному биту кодируемого слова. В каждом столбце матрицы преобразования поместим двоичный номер этого столбца, причём порядок следования битов будет обратный — младший бит расположим в верхней строке, старший — в нижней. Например, в третьем столбце матрицы будут стоять числа 11000, что соответствует двоичной записи числа три: 00011.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
В правой части таблицы мы оставили пустым один столбец, в который поместим результаты вычислений контрольных битов. Вычисление контрольных битов производим следующим образом. Берём одну из строк матрицы преобразования (например, r0) и находим её скалярное произведение с кодовым словом, то есть перемножаем соответствующие биты обеих строк и находим сумму произведений. Если сумма получилась больше единицы, находим остаток от его деления на 2. Иными словами, мы подсчитываем сколько раз в кодовом слове и соответствующей строке матрицы в одинаковых позициях стоят единицы и берём это число по модулю 2.
Если описывать этот процесс в терминах матричной алгебры, то операция представляет собой перемножение матрицы преобразования на матрицу-столбец кодового слова, в результате чего получается матрица-столбец контрольных разрядов, которые нужно взять по модулю 2.
Например, для строки r0:
r0 = (1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·1+0·1+1·1+0·0+1·0+0·0+1·0+0·1) mod 2 = 5 mod 2 = 1.
Полученные контрольные биты вставляем в кодовое слово вместо стоявших там ранее нулей. По аналогии находим проверочные биты в остальных строках. Кодирование по Хэммингу завершено. Полученное кодовое слово — 11110010001011110001.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Алгоритм декодирования по Хэммингу абсолютно идентичен алгоритму кодирования. Матрица преобразования соответствующей размерности умножается на матрицу-столбец кодового слова и каждый элемент полученной матрицы-столбца берётся по модулю 2. Полученная матрица-столбец получила название «матрица синдромов». Легко проверить, что кодовое слово, сформированное в соответствии с алгоритмом, описанным в предыдущем разделе, всегда даёт нулевую матрицу синдромов.
Матрица синдромов становится ненулевой, если в результате ошибки (например, при передаче слова по линии связи с шумами) один из битов исходного слова изменил своё значение. Предположим для примера, что в кодовом слове, полученном в предыдущем разделе, шестой бит изменил своё значение с нуля на единицу (на рисунке обозначено красным цветом). Тогда получим следующую матрицу синдромов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r0 | r1 | x1 | r2 | x2 | x3 | x4 | r3 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | r4 | x12 | x13 | x14 | x15 | ||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | s0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | s1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | s2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | s3 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | s4 | 0 |
Заметим, что при однократной ошибке матрица синдромов всегда представляет собой двоичную запись (младший разряд в верхней строке) номера позиции, в которой произошла ошибка. В приведённом примере матрица синдромов (01100) соответствует двоичному числу 00110 или десятичному 6, откуда следует, что ошибка произошла в шестом бите.