код хемминга сколько ошибок обнаруживает
Кодирование с помощью кода Хэмминга
Теоретическая часть
Для этого используются k – контрольных розрядов. И так если у нас задача закодировать m двоичных разрядов, то k должно удовлетворять неравенство 2k ≥ k+m+1 или k ≥ log2(k+m+1)
Таким образом мы можем найти минимальные значения k для заданных m: 
Теперь, мы можем построить самокорректирующийся код m+k разрядов. Приступим.
Запишем эти разряды и пронумеруем в двоичной системе.
Будем считать, что разряд принадлежит n-той контрольной группе, если в двоичном представлении эго номера стоит единица в n-том разряде.
Среди m+k разрядов мы будем иметь k разрядов, которые принадлежат только одной группе (степени двойки, так как они в двоичном представлении имеют только одну единицу).
Эти k разрядов мы будем считать контрольными. Остальные m разрядов будут информационными разрядами.
В информационные разряды переписываем наши исходные m разрядов.
В каждый из контрольных разрядов запишем такую цифру (0 или 1), чтоб общее количество единиц в его контрольной группе была парной. Для этого нам надо просто просуммировать по модулю два двоичных представления тех информационных разрядов, в которых стоит единица. Таким образом, мы узнаем контрольные разряды, ну и соответственно все m+k закодированных разрядов.
Пример
Давайте рассмотрим пример.
Например, нам дана последовательность 1001000. В данном случае m = 7, значит k = 4.
Запишем наши m + k разряды.

Узнаем теперь контрольные разряды:

Запишем контрольные разряды. 
Таким образом получаем закодированную последовательность 01100010000
Реализация
$input = «1001000» ; // задаем последовательость
$m = strlen($input); // узнаем длину
$result = Array(); // заводим массив разрядов
Избыточное кодирование, код Хэмминга
Избыточное кодирование (англ. redundant encoding) — вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.
| Определение: |
| Код определяет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования скажет, что есть ошибка. |
| Определение: |
| Код исправляет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования сможет восстановить исходное слово. |
Содержание
Код, определяющий одну ошибку [ править ]
Кодирование Хэмминга [ править ]
| [math]a[/math] | [math]b[/math] | [math]a \oplus b[/math] |
|---|---|---|
| [math]c[/math] | [math]d[/math] | [math]c \oplus d[/math] |
| [math]a \oplus c[/math] | [math] b \oplus d [/math] |
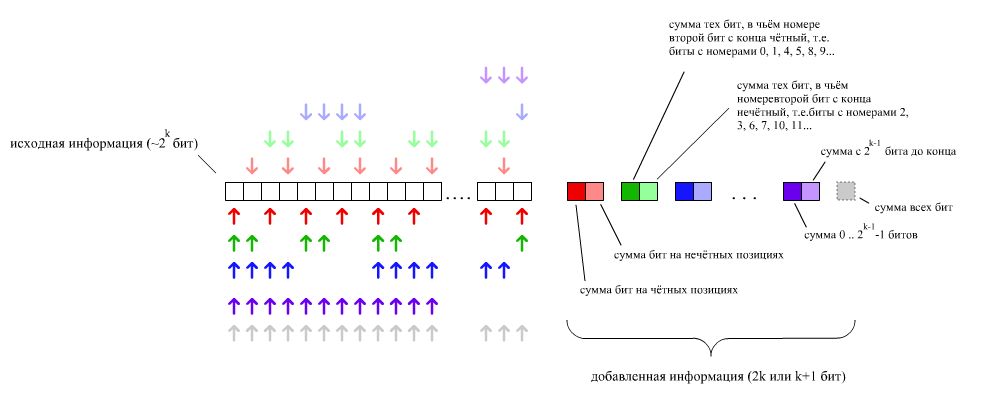
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в [math]2^k[/math] бит. Для получения её кода добавим к ней [math]k[/math] пар бит по следующему принципу:
Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит — [math] \mathrm X \mathrm O \mathrm R[/math] всех битов строки.
Определение и устранение ошибок в общем случае [ править ]
Пусть [math]\Sigma[/math] — исходный алфавит, [math]C: \Sigma \to B^m[/math] — кодирование, [math]B=(0,1)[/math]
[math]d: B^m \times B^m \to \mathbb
Определим [math]d_0 = \min[/math] [math]
Тогда легко понять, что код, полученный преобразованием [math]C[/math] может исправлять [math]
СОДЕРЖАНИЕ
История
Коды до Хэмминга
До кодов Хэмминга использовался ряд простых кодов обнаружения ошибок, но ни один из них не был так эффективен, как коды Хэмминга, в том же объеме служебных данных.
Паритет
Более того, четность не указывает, какой бит содержит ошибку, даже если он может ее обнаружить. Данные должны быть полностью отброшены и повторно переданы с нуля. В зашумленной среде передачи успешная передача может занять много времени или может никогда не произойти. Однако, хотя качество проверки четности оставляет желать лучшего, поскольку он использует только один бит, этот метод приводит к наименьшим накладным расходам.
Код два из пяти
Повторение
Однако такие коды не могут правильно исправить все ошибки. В нашем примере, если канал переворачивает два бита и получатель получает 001, система обнаружит ошибку, но сделает вывод, что исходный бит равен 0, что неверно. Если мы увеличим размер битовой строки до четырех, мы сможем обнаружить все двухбитовые ошибки, но не сможем исправить их (количество битов четности четное); при пяти битах мы можем как обнаруживать, так и исправлять все двухбитовые ошибки, но не все трехбитные ошибки.
Более того, увеличение размера строки битов четности неэффективно, снижая пропускную способность в три раза в нашем исходном случае, а эффективность резко падает, когда мы увеличиваем количество дублирований каждого бита для обнаружения и исправления большего количества ошибок.
Описание
Если в сообщение включено больше исправляющих ошибок битов и если эти биты могут быть расположены так, что разные неправильные биты дают разные результаты ошибок, то плохие биты могут быть идентифицированы. В семибитном сообщении существует семь возможных однобитовых ошибок, поэтому три бита контроля ошибок потенциально могут указывать не только на то, что произошла ошибка, но и на то, какой бит вызвал ошибку.
Хэмминга интересовали сразу две проблемы: как можно больше увеличить расстояние и в то же время как можно больше увеличить скорость кода. В 1940-х годах он разработал несколько схем кодирования, которые значительно улучшили существующие коды. Ключом ко всем его системам было перекрытие битов четности, чтобы им удавалось проверять друг друга, а также данные.
Общий алгоритм
Алгоритм можно вывести из следующего описания:
Выбор четности, четной или нечетной, не имеет значения, но один и тот же выбор должен использоваться как для кодирования, так и для декодирования.
Это общее правило можно показать наглядно:
| Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | … | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Биты закодированных данных | p1 | p2 | d1 | p4 | d2 | d3 | d4 | p8 | d5 | d6 | d7 | d8 | d9 | d10 | d11 | p16 | d12 | d13 | d14 | d15 | ||
| Покрытие битов четности | p1 |  |  |  |  |  |  |  |  |  |  | |||||||||||
| p2 |  |  |  |  |  |  |  |  |  |  | ||||||||||||
| p4 |  |  |  |  |  |  |  |  |  | |||||||||||||
| p8 |  |  |  |  |  |  |  |  | ||||||||||||||
| p16 |  |  |  |  |  | |||||||||||||||||
Коды Хэмминга с дополнительной четностью (SECDED)
Коды Хэмминга имеют минимальное расстояние 3, что означает, что декодер может обнаруживать и исправлять одиночную ошибку, но он не может отличить двойную битовую ошибку некоторого кодового слова от одиночной битовой ошибки другого кодового слова. Таким образом, некоторые двухбитовые ошибки будут неправильно декодированы, как если бы они были одноразрядными ошибками, и поэтому останутся необнаруженными, если не будет предпринята попытка исправления.
Чтобы исправить этот недостаток, коды Хэмминга могут быть расширены дополнительным битом четности. Таким образом, можно увеличить минимальное расстояние кода Хэмминга до 4, что позволяет декодеру различать одиночные битовые ошибки и двухбитовые ошибки. Таким образом, декодер может обнаруживать и исправлять одиночную ошибку и в то же время обнаруживать (но не исправлять) двойную ошибку.
Этот расширенный код Хэмминга популярен в системах памяти компьютеров, где он известен как SECDED (сокращенно от « исправление одиночных ошибок», «обнаружение двойных ошибок» ). Особенно популярен код (72,64), усеченный (127,120) код Хэмминга плюс дополнительный бит четности, который имеет такие же объемы служебных данных, как и код четности (9,8).
Код Хэмминга. Пример работы алгоритма
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:
Стало:
Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее: 
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее: 
и для второй части:
Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно): 
Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину: 
Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.