код определяющий количество вариантов добраться до ступенек
Программа Python для подсчета путей, чтобы добраться до n-й ступени
Есть n лестниц, человек, стоящий внизу, хочет достичь вершины. Человек может подняться на 1 или 2 ступеньки одновременно. Подсчитайте количество способов, которыми человек может достичь вершины.
Рассмотрим пример, показанный на диаграмме. Значение n равно 3. Есть 3 способа достичь вершины. Диаграмма взята из пазлов Легче Фибоначчи
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная программа для поиска n-го числа Фибоначчи
# возвращает нет. способов добраться до лестницы
# Предоставлено Харшитом Агравалом
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная функция, используемая countWays
def countWaysUtil(n, m):
while i = m and i = n:
# Возвращает количество способов добраться до лестницы
# Предоставлено Харшитом Агравалом
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная функция, используемая countWays
def countWaysUtil(n, m):
res = [ 0 for x in range (n)] # Создает список со всеми элементами 0
while j = m and j = i:
# Возвращает количество способов добраться до лестницы
# Предоставлено Харшитом Агравалом
Пожалуйста, обратитесь к полной статье о способах подсчета, чтобы добраться до n-й ступени, чтобы узнать больше!
Посчитай способы добраться до n-й ступени
Есть n лестниц, человек, стоящий внизу, хочет достичь вершины. Человек может подняться на 1 или 2 ступеньки одновременно. Подсчитайте количество способов, которыми человек может достичь вершины.
Рассмотрим пример, показанный на диаграмме. Значение n равно 3. Есть 3 способа достичь вершины. Диаграмма взята из пазлов Легче Фибоначчи
Больше примеров:
путей (1) = фиб (2) = 1
пути (2) = фиб (3) = 2
пути (3) = фиб (4) = 3
Таким образом, мы можем использовать функцию для чисел Фибоначчи, чтобы найти значение путей (n). Ниже приводится реализация вышеуказанной идеи на C ++.
// Простая рекурсивная программа для поиска n-го числа Фибоначчи
return fib(n-1) + fib(n-2);
// Возвращает количество способов добраться до лестницы
int countWays( int s)
// Программа драйвера для проверки вышеуказанных функций
// Простая рекурсивная программа для поиска n-го числа Фибоначчи
static int fib( int n)
return fib(n- 1 ) + fib(n- 2 );
// Возвращает количество способов добраться до лестницы
static int countWays( int s)
/ * Программа драйвера для проверки вышеуказанной функции * /
public static void main (String args[])
System.out.println( «Number of ways = » + countWays(s));
> / * Этот код предоставлен Раджатом Мишрой * /
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная программа для поиска n-го числа Фибоначчи
# возвращает нет. способов добраться до лестницы
# Предоставлено Харшитом Агравалом
// C # программа для подсчета
// количество способов достичь
// н ая лестница
// программа для поиска n
static int fib( int n)
// Возвращает количество способов
// чтобы добраться до лестницы
static int countWays( int s)
static public void Main ()
Console.WriteLine( «Number of ways = » +
// Этот код добавлен
// от akt_mit
// Простая рекурсивная
// функция для поиска n
// число Фибоначчи
// Возвращает количество
// способы добраться до лестницы
// Этот код добавлен
// от m_kit
?>
Выход:
Обобщение вышеуказанной проблемы
Как посчитать количество способов, если человек может подняться до m ступеней по заданному значению m? Например, если m равно 4, человек может одновременно подниматься на 1 ступеньку, 2 ступеньки, 3 ступеньки или 4 ступеньки.
Мы можем написать повторение следующим образом.
Ниже приводится реализация вышеупомянутых повторений.
// AC программа для подсчета количества способов добраться до лестницы, когда
// человек может подниматься на 1 или 2 ступеньки одновременно
#include
// Рекурсивная функция, используемая countWays
int countWaysUtil( int n, int m)
res += countWaysUtil(n-i, m);
// Возвращает количество способов добраться до лестницы
int countWays( int s, int m)
return countWaysUtil(s+1, m);
// Программа драйвера для проверки вышеуказанных функций
// Рекурсивная функция, используемая countWays
static int countWaysUtil( int n, int m)
res += countWaysUtil(n-i, m);
// Возвращает количество способов добраться до лестницы
static int countWays( int s, int m)
/ * Программа драйвера для проверки вышеуказанной функции * /
public static void main (String args[])
System.out.println( «Number of ways = » + countWays(s,m));
> / * Этот код предоставлен Раджатом Мишрой * /
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная функция, используемая countWays
while i = m and i = n:
# Возвращает количество способов добраться до лестницы
# Предоставлено Харшитом Агравалом
// C # программа для подсчета путей достижения
// н-й ступень
// Рекурсивная функция, используемая
static int countWaysUtil( int n, int m)
res += countWaysUtil(n-i, m);
// Возвращает количество способов достижения
static int countWays( int s, int m)
return countWaysUtil(s+1, m);
/ * Программа драйвера для проверки вышеуказанной функции * /
public static void Main ()
Console.Write( «Number of ways = «
// Этот код предоставлен нитин митталь.
// PHP-программа для подсчета
// количество способов достичь
// н ая ступенька, когда человек
// может подняться либо на 1, либо на 2
// лестницы за один раз
// рекурсивная функция
// используется countWays
// Возвращает количество способов
// чтобы добраться до лестницы
// Этот код добавлен
// от akt_mit
?>
Выход:
Временная сложность вышеуказанного решения является экспоненциальной. Его можно оптимизировать до O (mn) с помощью динамического программирования. Ниже приводится решение на основе динамического программирования. Мы строим таблицу res [] снизу вверх.
// Рекурсивная функция, используемая countWays
int countWaysUtil( int n, int m)
// Возвращает количество способов добраться до лестницы
int countWays( int s, int m)
return countWaysUtil(s+1, m);
// Программа драйвера для проверки вышеуказанных функций
// Рекурсивная функция, используемая countWays
static int countWaysUtil( int n, int m)
int res[] = new int [n];
res[ 0 ] = 1 ; res[ 1 ] = 1 ;
// Возвращает количество способов добраться до лестницы
static int countWays( int s, int m)
public static void main(String[] args)
System.out.println( «Nuber of ways = » + countWays(s, m));
# Программа для подсчета количества способов добраться до n ступени
# Рекурсивная функция, используемая countWays
res = [ 0 for x in range (n)] # Создает список со всеми элементами 0
while j = m and j = i:
# Возвращает количество способов добраться до лестницы
# Предоставлено Харшитом Агравалом
static int countWaysUtil( int n, int m)
int []res = new int [n];
// Возвращает количество способов
// чтобы добраться до лестницы
static int countWays( int s, int m)
return countWaysUtil(s + 1, m);
public static void Main()
Console.WriteLine( «Number of ways = » + countWays(s, m));
// Этот код предоставлен anuj_67.
// Рекурсивная функция, используемая countWays
// Возвращает количество способов
// чтобы добраться до лестницы
// Этот код предоставлен m_kit
?>
Опасные ступеньки: количество способов
Вася каждый день поднимается по одной и той же лестнице. Одним шагом он может встать на следующую ступеньку или перешагнуть через одну ступеньку. Он уже знает, сколькими способами он может подняться на верхнюю ступеньку. Но недавно он обнаружил, что некоторые ступеньки обветшали, и ступать на них небезопасно. Он составил список таких ступенек, и теперь интересуется, сколькими способами можно подняться по лестнице, не наступая на эти ступеньки.
Входные данные
В первой строке вводится одно натуральное число N (N ≤ 40): количество ступенек.
Во второй строке вводится одно натуральное число K (K ≤ N): количество опасных ступенек.
В третьей строке вводятся K различных натуральных чисел в диапазоне от 1 до N: номера опасных ступенек.
Выходные данные
Выведите одно число: количество способов попасть на N-ю ступеньку.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Опасные ступеньки: количество способов
Задача: Вася каждый день поднимается по одной и той же лестнице. Одним шагом он может встать на.
Опасные ступеньки
Вася каждый день поднимается по одной и той же лестнице. Одним шагом он может встать на следующую.
Опасные ступеньки: количество способов
есть код,но проходит 9 из 15, помогите, пожалуйста условие: Вася каждый день поднимается по.
Определить сколькими способами можно подняться по лестнице, не наступая на опасные ступеньки
Вася каждый день поднимается по одной и той же лестнице. Одним шагом он может встать на следующую.
Вам нужно подняться по лестнице. За один раз можно подняться на одну или две ступеньки. Сколько существует способов добраться до N-й ступеньки?
Начало здесь простое. Вы стоите на лестничном марше и хотите подняться на первую ступеньку — № 1. Для этого надо сделать всего одно действие — подняться на одну ступеньку вверх. Теперь давайте рассмотрим вторую ступеньку, то есть N = 2. Чтобы подняться на неё, имеются два варианта. Вы можете сделать два шага — по одной ступеньке за раз или сразу подняться на вторую ступеньку.
Это практически вся информация, которая нужна вам для решения этой задачи. Чтобы понять, почему, представьте, что вашей целью является ступенька № 3. Впервые в этой ситуации вы не можете попасть на неё одним движением. здесь потребуется комбинация шагов. Существует только два способа попадания на ступеньку № 3: либо в виде короткого одиночного шага (со ступеньки № 2), либо двойного шага (со ступеньки № 1). Мы уже знаем, что для подъема на ступеньку № 1 имеется лишь один вариант. Мы также знаем, что есть всего два способа подняться на ступеньку № 2. Сложите эти варианты (1 + 2 = 3), и вы получите число способов, позволяющих подняться на ступеньку № 3.
Та же самая логика применяется для подъема на каждую следующую ступеньку. Существует два способа, чтобы подняться на ступеньку № 4 — со ступеньки № 2 или со ступеньки № 3. Добавьте число способов подъема на ступеньку № 2 (2) к числу способов, позволяющих оказаться на ступеньке № 3 (3). Это даёт 5 вариантов — число способов, позволяющих оказаться на ступеньке № 4.
Легко продолжить эту серию и дальше. С увеличением числа ступенек число способов подниматься по ним нарастает, как снежный ком, что можно представить в следующем виде:
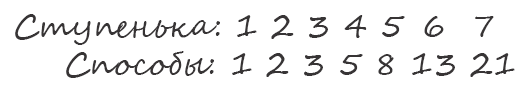
Это просто число Фибоначчи под номером N. Леонардо Фибоначчи, также известный как Леонардо Пизанский, был самым влиятельным итальянским математиком в Средние века. Именно Фибоначчи понял невероятное превосходство арабскo-индийской позиционной системы исчисления по сравнению с римским обозначением цифр, которое все ещё использовалось в средневековой Европе. При помощи арабско-индийской системы умножение и деление можно было свести к алгоритму (еще одно арабское слово). При применении римских чисел эти операции на практике выполнять было сложно. Торговцам приходилось приглашать экспертов и дорого им платить за вычисления, которые те осуществляли при помощи абаков. В 1202 году Фибоначчи написал Liber abaci — руководство по использованию абака, в котором он расхваливал арабские числа своим читателям, которые были, скорее всего, настроены к ним скептически. В этой книге также описывается и та серия чисел, которую мы теперь называем по его фамилии. Однако её изобрел не Фибоначчи. Эта последовательность была известна еще индийским ученым, жившим в VI веке.
Напишите 1, а затем добавьте еще 1 рядом. Сложите их и получите сумму (2), которая затем добавляется к формируемой последовательности:
Для получения каждого нового члена лишь складывайте последние два числа в ряду/ Серия примет следующий вид.
1 1 2 3 5 8 13 21 34 55 89 144…
Поклонники теории заговоров отыскивают серии Фибоначчи в самых неожиданных местах. Хотите перевести расстояние из миль в километры? Воспользуйтесь соседними числами Фибоначчи (55 миль в час = 89 километров в час). В следующий раз, когда у вас окажется свободное время, посчитайте небольшие дольки, из которых состоит кожура ананаса, и вы обнаружите, что они образуют два накладывающихся друг на друга набора спиралей, идущих в противоположных направлениях. В одной из них восемь долей, в другой тринадцать. Оба этих числа относятся к серии Фибоначчи. Аналогичные закономерности можно увидеть в сосновых шишках, подсолнухах и артишоках. Случайность? Вряд ли, если учесть тот факт, что последовательность Фибoначчи проявила себя и в Коде Да Винчи (в виде комбинации для вскрытия сейфа), и в этом вопросе на собеседовании, который задают в компании, стремящейся к информационному доминированию во всем мире (Google, если вы не поняли).
Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.
Перейти к регистрации
сколько различных способов есть у зайца добраться до вершины лестницы при заданных значениях K и N
Доброго времени суток, уважаемые форумчане!
Есть задача:
В нашем зоопарке появился заяц. Его поместили в клетку, и чтобы ему не было скучно, директор зоопарка распорядился поставить в его клетке лесенку. Теперь наш зайчик может прыгать по лесенке вверх, перепрыгивая через ступеньки. Лестница имеет определенное количество ступенек N. Заяц может одним прыжком преодолеть не более К ступенек. Для разнообразия зайчик пытается каждый раз найти новый путь к вершине лестницы. Директору любопытно, сколько различных способов есть у зайца добраться до вершины лестницы при заданных значениях K и N. Помогите директору написать программу, которая поможет вычислить это количество. Например, если K=3 и N=4, то существуют следующие маршруты: 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2, 1+3, 3+1. Т.е. при данных значениях у зайца всего 7 различных маршрутов добраться до вершины лестницы.
В единственную строку выходного файла OUTPUT.TXT нужно вывести количество возможных вариантов различных маршрутов зайца на верхнюю ступеньку лестницы без ведущих нулей.
Примеры
INPUT.TXT OUTPUT.TXT
1 3 1
2 7 21
3 10 274[/SIZE][/QUOTE]
Так же нашел решение. Все работает, но не понимаю как это работает =)
Приведу пример, где k=3, n=4. Значит формула должна выглядеть так:
Заранее спасибо. Целый день сегодня бьюсь ((
Помощь в написании контрольных, курсовых и дипломных работ здесь.


