код прюфера для дерева код
Код Прюфера
Деревья. Кратко напомним
Дерево – частный случай графа. Деревья широко применяются в программировании. Дерево – это связный граф без циклов. Дерево называется помеченным, если каждой вершине соответствует уникальная метка. Обычно это число.
Определение. Построение кода Прюфера для заданного дерева
Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.
Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.
Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.
На вход подается список ребер. Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом. Эта процедура повторяется n-2 раза. В конце концов, в дереве останется только 2 вершины, и алгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.
Таким образом, код Прюфера для заданного дерева – это последовательность из n-2 чисел, где каждое число – номер вершины, связанной с наименьшим на тот момент листом – то есть это число в отрезке [1,n].
Пример
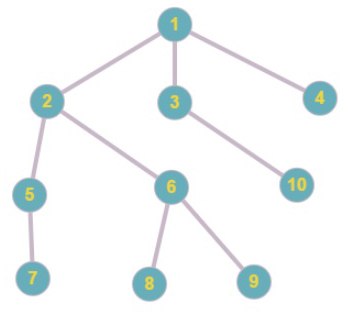
Исходное дерево
Код Прюфера: 1
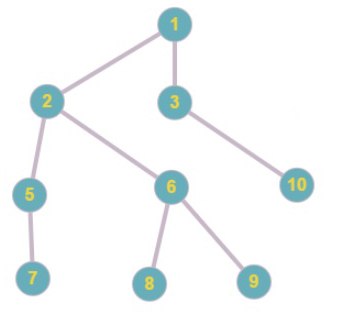
Код Прюфера: 1 5
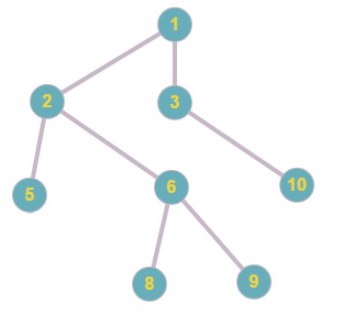
Код Прюфера: 1 5 2
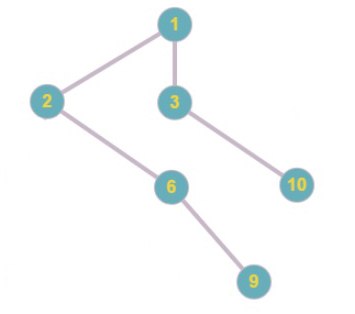
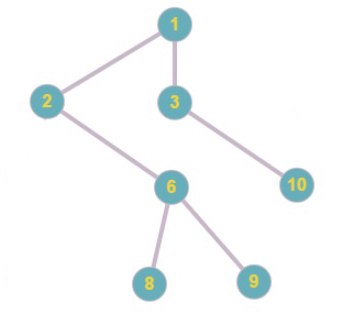
Код Прюфера: 1 5 2 6
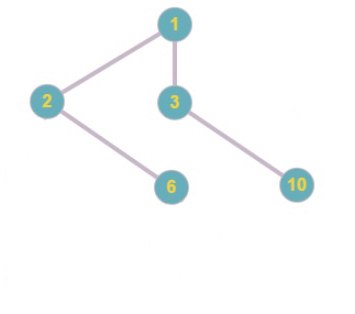
Код Прюфера: 1 5 2 6 6
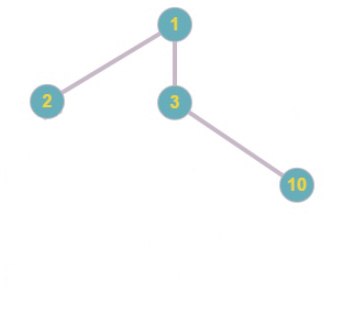
Код Прюфера: 1 5 2 6 6 2
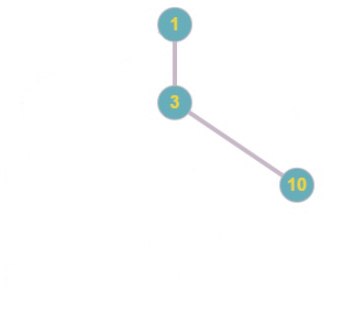
Код Прюфера: 1 5 2 6 6 2 1
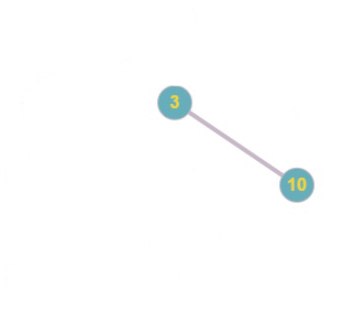
Код Прюфера: 1 5 2 6 6 2 1 3
Восстановление дерева по его коду Прюфера
Рядом с задачей построения кода Прюфера стоит задача восстановления закодированного дерева. Будем рассматривать алгоритм восстановления дерева со следующими условиями: на вход подается последовательность цифр (вершин), которая представляет код Прюфера, результатом будет список ребер дерева. Таким образом, задача будет решена.
Рассмотрим алгоритм декодирования подробно. Помимо кода нам нужен список всех вершин графа. Мы знаем, что код Прюфера состоит из n-2 вершин, где n – это число вершин в графе. То есть, мы можем по размеру кода определить число вершин в закодированном дереве.
В результате, в начале работы алгоритма мы имеем массив из кода Прюфера размера n-2 и массив всех вершин графа: [1… n]. Далее n-2 раза повторяется такая процедура: берется первый элемент массива, содержащего код Прюфера, и в массиве с вершинами дерева производится поиск наименьшей вершины, не содержащейся в массиве с кодом. Найденная вершина и текущий элемент массива с кодом Прюфера составляют ребро дерева. Данные вершины удаляются из соответствующих массивов, и описанная выше процедура повторяется, пока в массиве с кодом не закончатся элементы. В конце работы алгоритма в массиве с вершинами графа останется две вершины, они составляют последнее ребро дерева. В результате получаем список всех ребер графа, который был закодирован.
Пример
Восстановим дерево по коду Прюфера, который был получен в примере кодирования.
Первый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 4
Список ребер: 1 4
Второй шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 7
Список ребер: 1 4, 5 7
Третий шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 5
Список ребер: 1 4, 5 7, 2 5
Четвертый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 8
Список ребер: 1 4, 5 7, 2 5, 6 8
Пятый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 9
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9
Шестой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 6
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6
Седьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 2
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2
Восьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1
Завершение алгоритма
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10
Заключение
Код Прюфера был предложен как наглядное и простое доказательство формулы Кэли о числе помеченных деревьев. На практике же его используют чаще для решения комбинаторных задач.
Источники
Тема 7.7 Деревья. Код Пруфера
Деревом называется всякий несвязный граф без циклов.
 |
Граф, состоящий из изолированной вершины, тоже считается деревом.
Вершина дерева, степень которой равна 1, называется висячей.
Лесом называется граф представленный в виде объединения деревьев.
Теорема: Если у дерева n вершин, то ребер n-1.
Рассмотрим произвольное дерево с 11 вершинами, пронумерованными в произвольном порядке.
 |  |
В результате возникает вопрос: сколько существует таких деревьев с 11 вершинами?
Немецкий математик Пруффер продолжил решать эту проблему и указал алгоритм, согласно которому любому дереву можно поставить во взаимно-однозначное соответствие – код.
1. выбираем висячую вершину с наименьшим номером.
2. удаляем ее вместе с принадлежащим ей ребром.
3. записываем номер вершины полученного дерева ближайшей к удаленной.
4. 
2. записываем вершину № 1
3. выбираем вершину № 3
4. записываем вершину № 1
и т.д., в результате получаем код: (1, 1, 5, 5, 6, 6, 6, 6, 5)
И наоборот, зная код можно изобразить дерево.
Алгоритм составления дерева по коду:
1. находим наименьшее натуральное число, которое не встречается в последовательности.
2. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.
3. находим следующее число
Дан код (1, 5, 5, 3, 6, 4).
Количество вершин = 8,
1. наименьшее число, не встречающееся в последовательности – 2
2. строим эту вершину и соединяем ребром с вершиной №1
3. аналогично перебираем все цифры не встречающиеся в последовательности до 8.
 |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Код Прюфера
Деревья. Кратко напомним
Дерево – частный случай графа. Деревья широко применяются в программировании. Дерево – это связный граф без циклов. Дерево называется помеченным, если каждой вершине соответствует уникальная метка. Обычно это число.
Определение. Построение кода Прюфера для заданного дерева
Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.
Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.
Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.
На вход подается список ребер. Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом. Эта процедура повторяется n-2 раза. В конце концов, в дереве останется только 2 вершины, и алгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.
Таким образом, код Прюфера для заданного дерева – это последовательность из n-2 чисел, где каждое число – номер вершины, связанной с наименьшим на тот момент листом – то есть это число в отрезке [1,n].
Пример 
Исходное дерево 
Код Прюфера: 1 
Код Прюфера: 1 5 
Код Прюфера: 1 5 2 
Код Прюфера: 1 5 2 6 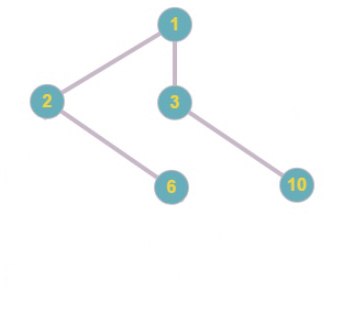
Код Прюфера: 1 5 2 6 6 
Код Прюфера: 1 5 2 6 6 2 
Код Прюфера: 1 5 2 6 6 2 1 
Код Прюфера: 1 5 2 6 6 2 1 3
Восстановление дерева по его коду Прюфера
Рядом с задачей построения кода Прюфера стоит задача восстановления закодированного дерева. Будем рассматривать алгоритм восстановления дерева со следующими условиями: на вход подается последовательность цифр (вершин), которая представляет код Прюфера, результатом будет список ребер дерева. Таким образом, задача будет решена.
Рассмотрим алгоритм декодирования подробно. Помимо кода нам нужен список всех вершин графа. Мы знаем, что код Прюфера состоит из n-2 вершин, где n – это число вершин в графе. То есть, мы можем по размеру кода определить число вершин в закодированном дереве.
В результате, в начале работы алгоритма мы имеем массив из кода Прюфера размера n-2 и массив всех вершин графа: [1… n]. Далее n-2 раза повторяется такая процедура: берется первый элемент массива, содержащего код Прюфера, и в массиве с вершинами дерева производится поиск наименьшей вершины, не содержащейся в массиве с кодом. Найденная вершина и текущий элемент массива с кодом Прюфера составляют ребро дерева. Данные вершины удаляются из соответствующих массивов, и описанная выше процедура повторяется, пока в массиве с кодом не закончатся элементы. В конце работы алгоритма в массиве с вершинами графа останется две вершины, они составляют последнее ребро дерева. В результате получаем список всех ребер графа, который был закодирован.
Пример
Восстановим дерево по коду Прюфера, который был получен в примере кодирования.
Первый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 4
Список ребер: 1 4
Второй шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 7
Список ребер: 1 4, 5 7
Третий шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 5
Список ребер: 1 4, 5 7, 2 5
Четвертый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 8
Список ребер: 1 4, 5 7, 2 5, 6 8
Пятый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 9
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9
Шестой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 6
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6
Седьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 2
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2
Восьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1
Завершение алгоритма
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10
Заключение
Код Прюфера был предложен как наглядное и простое доказательство формулы Кэли о числе помеченных деревьев. На практике же его используют чаще для решения комбинаторных задач.
Алгоритм построения кода Прюфера по дереву
Вход: дерево с n вершинами.
Выход: код Прюфера длины n – 2.
Повторить n – 2 раза
Выбрать вершину v – лист дерева с наименьшим номером;
Добавить номер единственного соседа v в последовательность кода Прюфера;
Удалить вершину v из дерева;
Пример 1. Построение всех кодов Прюфера длины 2. Для этого следует рассмотреть все возможные деревья из 4 вершин. Под каждым деревом приведен соответствующий код.
Алгоритм составления дерева по коду:
1.Выписываем висячие вершины, всего вершин на 2 больше чем значений в коде дерева.
2. находим наименьшее натуральное число, которое не встречается в последовательности.
3. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.
4. находим следующее число.
Рассмотрим применение данного алгоритма на примере.
Пример 1. Постройте дерево, которому соответствует код
1. Выписываем висячие вершины. Всего вершин на 2 больше чем значений в коде дерева, в данном случае такими будут 3,4,5,6,7.
2. Вершину с минимальным номером (3) соединяем с первым значением кода (1).
Дальше вершины (2) больше нет в коде, потому она становится висячей с наименьшим номером, потому следующим шагом я соединяю ее (2) со следующим значением кода (1).
Далее 6 – 7. Код закончился, осталась 6. Соединяем ее с 1.
Задана матрица инцидентности неориентированного графа G:
Тема 7.7 Деревья. Код Пруфера
Деревом называется всякий несвязный граф без циклов.
 |
Граф, состоящий из изолированной вершины, тоже считается деревом.
Вершина дерева, степень которой равна 1, называется висячей.
Лесом называется граф представленный в виде объединения деревьев.
Теорема: Если у дерева n вершин, то ребер n-1.
Рассмотрим произвольное дерево с 11 вершинами, пронумерованными в произвольном порядке.
 |  |
В результате возникает вопрос: сколько существует таких деревьев с 11 вершинами?
Немецкий математик Пруффер продолжил решать эту проблему и указал алгоритм, согласно которому любому дереву можно поставить во взаимно-однозначное соответствие – код.
1. выбираем висячую вершину с наименьшим номером.
2. удаляем ее вместе с принадлежащим ей ребром.
3. записываем номер вершины полученного дерева ближайшей к удаленной.
4. 
2. записываем вершину № 1
3. выбираем вершину № 3
4. записываем вершину № 1
и т.д., в результате получаем код: (1, 1, 5, 5, 6, 6, 6, 6, 5)
И наоборот, зная код можно изобразить дерево.
Алгоритм составления дерева по коду:
1. находим наименьшее натуральное число, которое не встречается в последовательности.
2. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.
3. находим следующее число
Дан код (1, 5, 5, 3, 6, 4).
Количество вершин = 8,
1. наименьшее число, не встречающееся в последовательности – 2
2. строим эту вершину и соединяем ребром с вершиной №1
3. аналогично перебираем все цифры не встречающиеся в последовательности до 8.
 |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
