код знака перпендикулярности в ворде
Значок перпендикулярности в ворде
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Вопрос решен и закрыт.
Лучший ответ
Енот 8 (337417) 6 26 633 6 лет
Ответы
FighteR (30) 7 (88378) 7 26 967 6 лет
ПРОЖЕКТОР 6 (9106) 3 13 43 6 лет
Ylarya 6 (6586) 2 4 15 6 лет
Vadinho 6 (16535) 3 41 85 6 лет
Похожие вопросы
Это лого фирмы Ямаха. 3 скрещённых камертона (небольшой портативный прибор, точно и ясно издающий звук определённой высоты со слабыми гармоническими призвуками.)
Скорее всего на уроках музыки вам это рассказывали.
Для обозначения перпендикулярности имеется общепринятый символ: ⊥ 
, предложенный в 1634 году французским математиком Пьером Эригоном. Например, перпендикулярность прямых m и n записывают как m ⊥ n .
Содержание
На плоскости [ править | править код ]
Перпендикулярные прямые на плоскости [ править | править код ]
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую m перпендикулярную к прямой ℓ проведённую через точку P вне прямой ℓ , говорят, что m есть перпендикуляр опущенный из P на ℓ . Если же точка P лежит на прямой ℓ , то говорят, что m есть перпендикуляр к восстановленный из P к ℓ (устаревший термин восставленный [1] ).
В координатах [ править | править код ]
В аналитическом выражении прямые, заданные линейными функциями
y = a ⋅ x + b
y = k ⋅ x + m
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
a ⋅ k = − 1.
Построение перпендикуляра [ править | править код ]
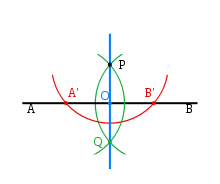
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.
Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой [ править | править код ]
Если x a = x b (вертикаль), то x o = x a =x_> и y o = y p =y_
> . Если y a = y b (горизонталь), то x o = x p =x_
> и y o = y a =y_> .
Во всех остальных случаях:
x o = x a ⋅ ( y b − y a ) 2 + x p ⋅ ( x b − x a ) 2 + ( x b − x a ) ⋅ ( y b − y a ) ⋅ ( y p − y a ) ( y b − y a ) 2 + ( x b − x a ) 2 = +x_
-y_)> +(x_-x_)^ >>> ; y o = ( x b − x a ) ⋅ ( x p − x o ) ( y b − y a ) + y p = -x_)cdot (x_
> .
В трёхмерном пространстве [ править | править код ]
Перпендикулярные прямые [ править | править код ]
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямой к плоскости [ править | править код ]
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости [ править | править код ]
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
В многомерных пространствах [ править | править код ]
Перпендикулярность плоскостей в 4-мерном пространстве [ править | править код ]
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно ( 4 2 ) = 6 >=6> : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).
Перпендикулярность прямой и гиперплоскости [ править | править код ]
Прямая l называется перпендикулярной гиперплоскости Π k > , если подпространство L 1 > ортогонально подпространству L k > , то есть ( ∀ a → ∈ L 1 ) ( ∀ b → ∈ L k ) a → b → = 0 in L_ ) (forall in L_ ) =0>
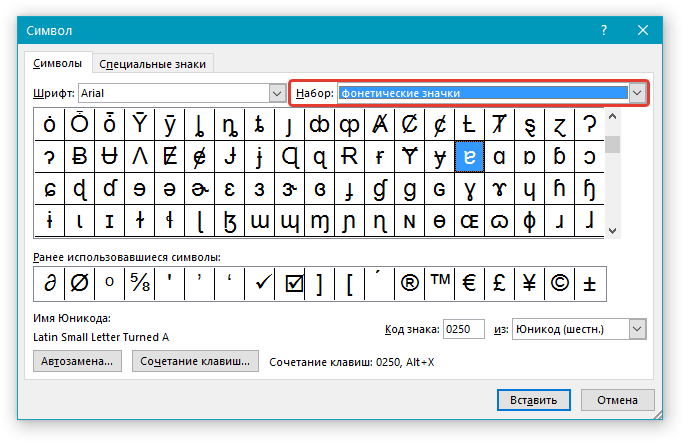
Знак перпендикулярности в ворде
Наборы с этим символом:
© Таблица символов Юникода, 2012–2020.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.
Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее
Таблица. Математические символы и греческие буквы
Лень искать код вставки — скопипасть отсюда.
В какой программе?
В Ворде сделать таблицу
тупо писать Т
потом указать метод ориентации букв — и перевернуть
Куча возможностей в любой проге.
Таки в какой же?
Математические тексты в научном сообществе принято набирать в TeX (LaTeX, XeLaTeX и т. д. ) Делается так:
Вероятнее всего, вы хотя бы раз сталкивались с необходимостью вставить в MS Word знак или символ, которого нет на компьютерной клавиатуре. Это могло быть, к примеру, длинное тире, символ градуса или правильной дроби, а также много чего другого. И если в некоторых случаях (тире и дроби) на помощь приходит функция автозамены, то в других все оказывается намного сложнее.
Мы уже писали о вставке некоторых специальных символов и знаков, в этой статье мы расскажем о том, как быстро и удобно добавлять в документ MS Word любые из них.
Вставка символа
1. Кликните в том месте документа, куда необходимо вставить символ.
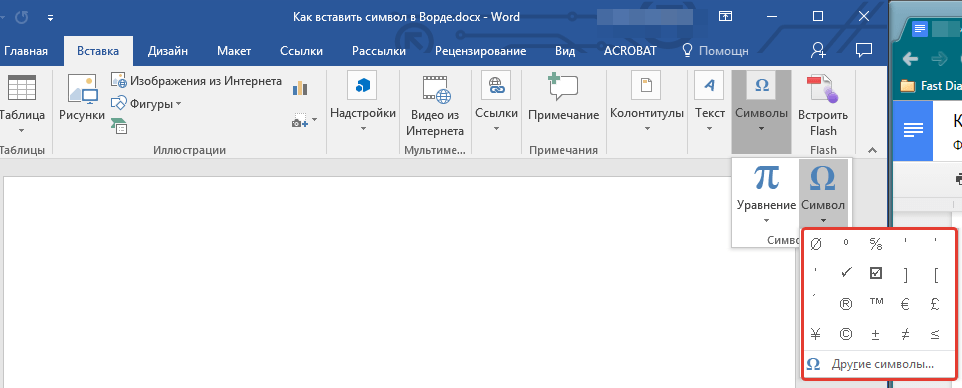
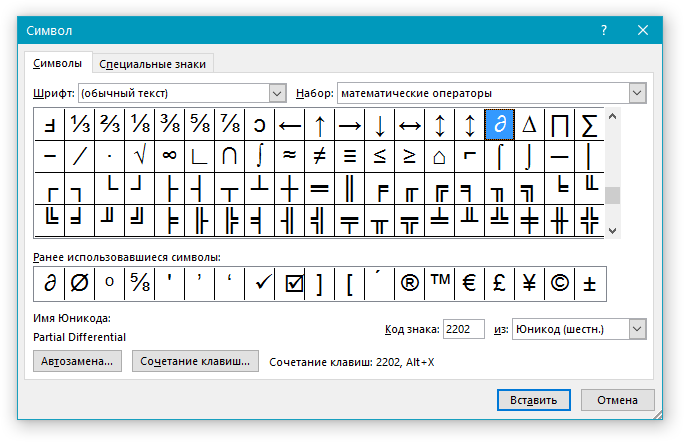
2. Перейдите во вкладку “Вставка” и нажмите там кнопку “Символ”, которая находится в группе “Символы”.
3. Выполните необходимое действие:
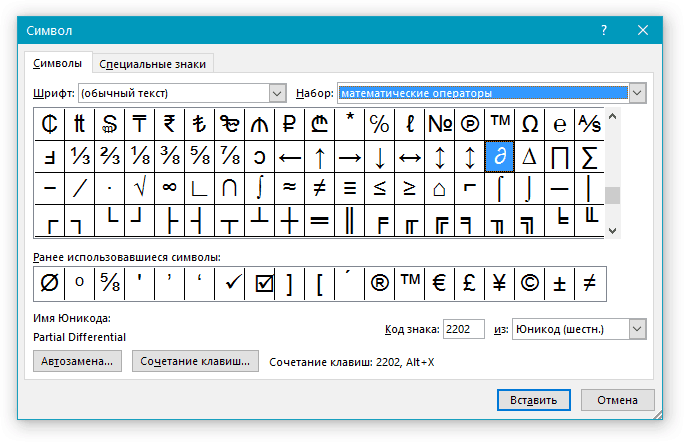
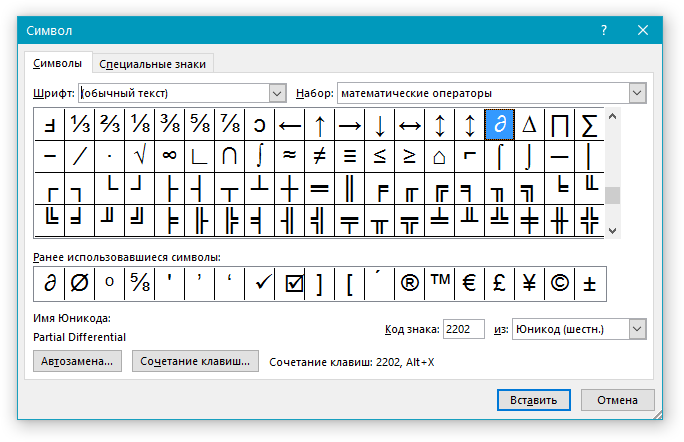
Примечание: В диалоговом окне “Символ” содержится очень много различных символов, которые сгруппированы по тематикам и стилям. Для того, чтобы быстрее найти нужный символ, вы можете в разделе “Набор” выбрать характерный для этого символа, например, “Математические операторы” для того, чтобы найти и вставить математические символы. Также, можно изменять шрифты в соответствующем разделе, ведь во многих из них тоже есть различные символы, отличные от стандартного набора.
4. Символ будет добавлен в документ.
Вставка специального знака
1. Кликните в том месте документа, куда необходимо добавить специальный знак.
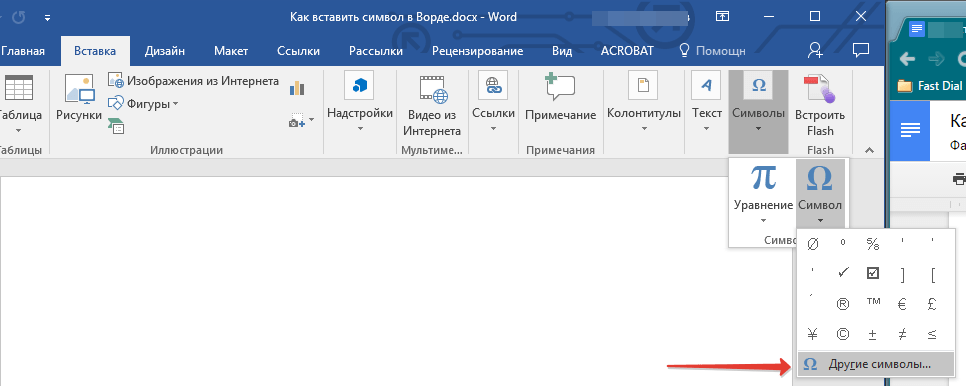
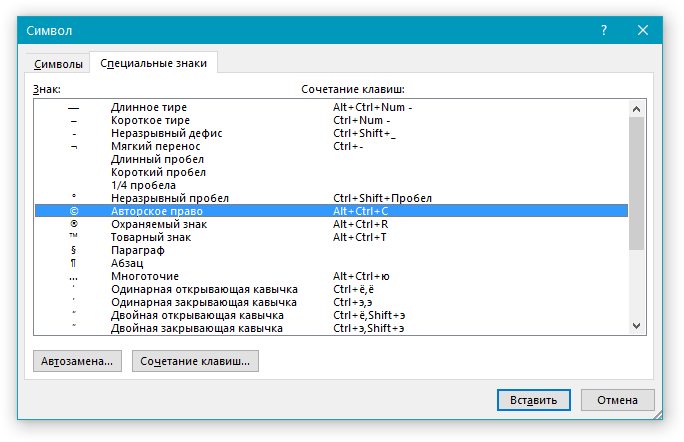
2. Во вкладке “Вставка” откройте меню кнопки “Символы” и выберите пункт “Другие символы”.
3. Перейдите во вкладку “Специальные знаки”.
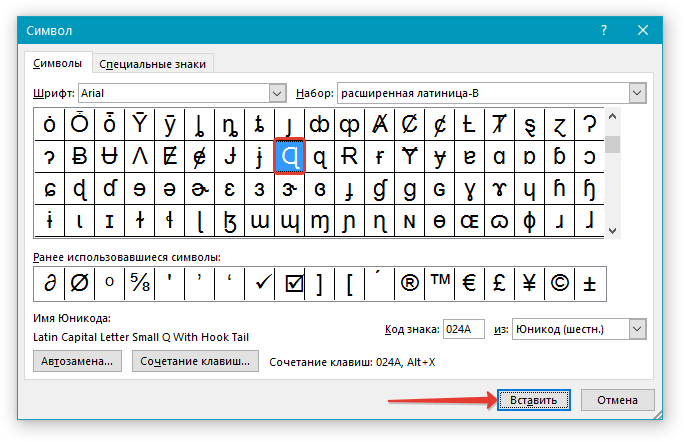
4. Выберите необходимый знак, кликнув по нему. Нажмите кнопку “Вставить”, а затем “Закрыть”.
5. Специальный знак будет добавлен в документ.
Примечание: Обратите внимание, что в разделе “Специальные знаки” окна “Символ”, помимо самих специальных знаков вы также можете увидеть горячие комбинации клавиш, которые можно использовать для их добавления, а также настроить автозамену для конкретного символа.
Вставка символов Юникода
Вставка знаков Юникода мало чем отличается от вставки символов и специальных знаков, за исключением одного важного преимущества, заметно упрощающего рабочий процесс. Более подробная инструкция о том, как это сделать, изложена ниже.
Выбор знака Юникода в окне “Символ”
1. Кликните в том месте документа, куда нужно добавить знак Юникода.
2. В меню кнопки “Символ” (вкладка “Вставка”) выберите пункт “Другие символы”.
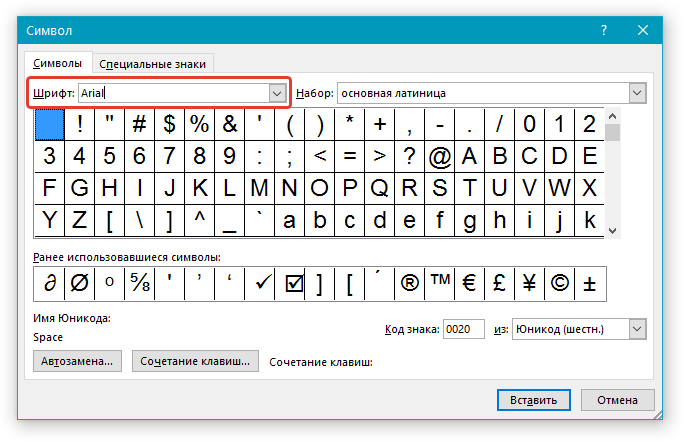
3. В разделе “Шрифт” выберите необходимый шрифт.
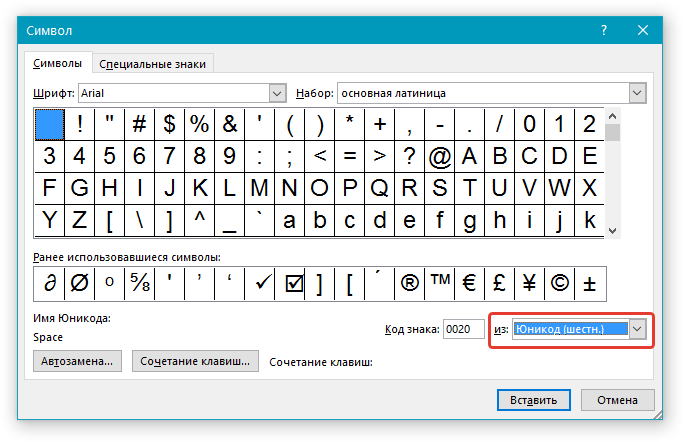
4. В разделе “Из” выберите пункт “Юникод (шестн)”.
5. Если поле “Набор” будет активно, выберите необходимый набор символов.
6. Выбрав нужный символ, кликните по нему и нажмите “Вставить”. Закройте диалоговое окно.
7. Знак Юникода будет добавлен в указанное вами место документа.
Урок: Как в Word поставить символ галочки
Добавление знака Юникода с помощью кода
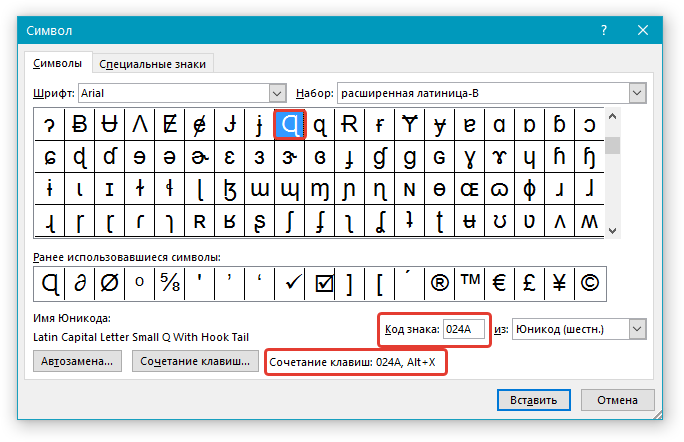
Как уже было сказано выше, у знаков Юникода есть одно важное преимущество. Заключается оно в возможности добавления знаков не только через окно “Символ”, но и с клавиатуры. Для этого необходимо ввести код знака Юникода (указан в окне “Символ” в разделе “Код”), а затем нажать комбинацию клавиш.
Очевидно, что запомнить все коды этих знаков невозможно, но самые необходимые, часто используемые выучить точно можно, ну, или хотя бы записать их где-нибудь и хранить под рукой.
1. Кликните левой кнопкой мышки там, где требуется добавить знак Юникода.
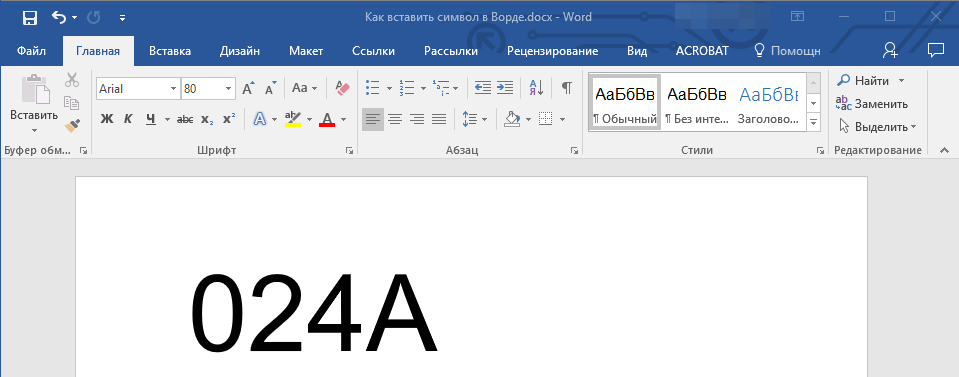
2. Введите код знака Юникода.
Примечание: Код знака Юникода в Word всегда содержит буквы, вводить их необходимо в английской раскладке заглавным регистром (большими).
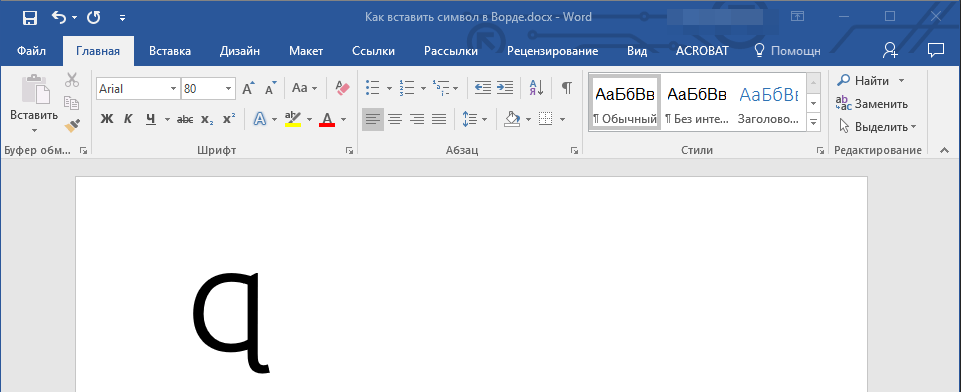
3. Не перемещая указатель курсора с этого места, нажмите клавиши “ALT+X”.
4. В указанном вами месте появится знак Юникода.
Вот и все, теперь вы знаете о том, как вставить в Майкрософт Ворд специальные знаки, символы или знаки Юникода. Желаем вам положительных результатов и высокой продуктивности в работе и обучении.
Вставка кодов символов ASCII или Юникода в Word
Вставка символа с помощью клавиатуры с кодами символов ASCII или Юникода
Символы и специальные знаки вставляются с помощью кодов ASCII или Юникода. Вы можете укассировать код при подытовом коде для знака.
Перейдите на вкладку > символ > другие символы.
Найдите нужный символ.
Совет: Шрифт Segoe UI Symbol содержит очень большой набор символов Юникода, которые можно выбрать.
В правой нижней части вы увидите код знака и от:. Код знака используется для вставки этого символа с клавиатуры. Поле «От»: указывает, является ли это кодом Юникода или символом ASCII.
Юникод
ASCII
Вставка символов Юникод
Введите код символа там, куда необходимо вставить знак в кодировке Юникод.
Нажмите клавиши ALT + X, чтобы преобразовать код в символ.
Если символ Юникода нужно поместить сразу после другого, выделите код, прежде чем нажимать ALT+X.
Совет: Если вы не получили символ, который вы ожидали, убедитесь в том, что выбран правильный шрифт.
Вставка символов ASCII
На цифровой клавиатуре с помощью клавиши Num Lock введите номера ASCII, а не номера в верхней части клавиатуры.
Все коды символов ASCII имеют четыре цифры. Если код символа меньше четырех цифр, добавьте нули в начале, чтобы получить 4 цифры.
На вкладке Главная в группе Шрифт измените шрифт на Wingdings (или другой набор шрифтов).
Нажмите клавишу ALT и, удерживая ее, введите код символа с помощью цифровой клавиатуры.
После вставки символа измените шрифт на предыдущий.
Департамент ИТ
Одно из основных правил для правильного создания документов в Word – правописание. Не поймите неправильно, так как это не имеет ничего общего с грамматикой или стилем написания.
Если вы хотите, чтобы Word красиво выравнивал текст и соблюдал интервалы между абзацами, то вы должны убедиться в том, что вы не ставили лишние пробелы между словами и в ячейках, что начало абзацев расположены правильно и отступы настроены так, что документ выглядит правильно оформленным.
Было бы очень трудоемко определить определенные пространства или места в документе, где использовалось случайное двойное нажатие TAB (ТАБУЛЯЦИЯ) вместо одного, если не было бы знаков форматирования. Эти знаки являются непечатающимися символами и показывают нам места, где были использованы клавиши SPACE (ПРОБЕЛ), TAB, ENTER (ВВОД), или где находится скрытый текст.
Без них было бы практически невозможно создать документ в правильном оформлении: это займет очень много времени, чтобы исправить ошибки, которые мешают правильному выравниванию текста и объектов.
Как правило, знаки форматирования скрыты, пока вы не сделаете их видимыми нажатием ¶ на вкладке «Главная» в Word (рис. 1).
Кроме того, вы можете использовать сочетания клавиш Ctrl + * или Ctrl + Shift + 8 для переключения «Показать\Скрыть» символов форматирования. Переключение отображения символов форматирования имеет два положения:
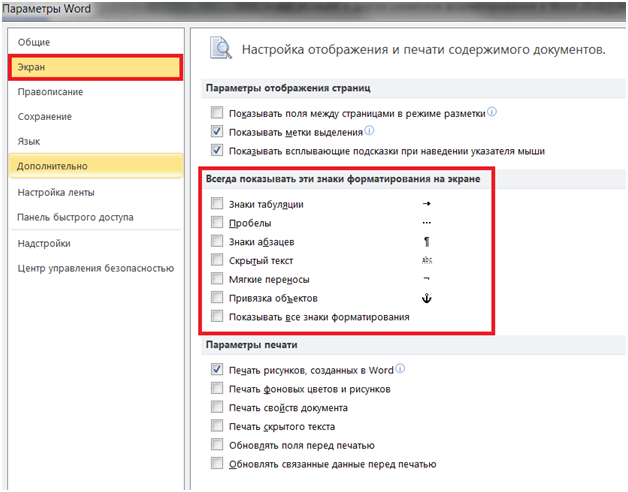
Нажмите «Экран» и с лева, под «Всегда показывать эти знаки форматирования» выберите какие знаки форматирования вы хотите сделать видимыми всегда, даже после отключения (рис. 3).
Существуют различные знаки форматирования, или иногда их называют непечатающимися символами, в Word. Рассмотрим основные из них.
Символ пробела
Точки это знаки форматирования пробелов между словами. Одно нажатие на пробел – одна точка (рис. 4).
Символ абзаца
Символ (¶) представляет собой конец абзаца. После этого символа Word начинает новый абзац и перемещает курсор на новую строку (рис. 5).
Знак абзаца помещается в документе при нажатии клавиши Enter на вашей клавиатуре. Текст между двумя этими символами определяется как абзац и имеет ряд свойств, которые можно регулировать независимо от остального текста (или абзацев), такие как выравнивание (по левому и правому краям, по центру и ширине), интервалы перед и после абзаца, интервалы между строками, нумерация и др.
Знак табуляции
Нажатие табуляции (TAB) отображается знаком стрелки, направленной вправо (рис. 6):
Перевод строки
Знак перевода строки или 
представляет собой место, где строка обрывается и текст продолжается с новой строки. Вы можете вставить перевод строки, нажав Shift+Enter.
Функции знака перевода строки во многом схожи со знаком абзаца и имеет аналогичный эффект, за исключением, что при переводе строки не определяются новые абзацы (рис. 7).
Скрытый текст
Скрытый текст представляет собой пунктирную линию под текстом, который определен как скрытый (рис. 8).
Когда вы отключите знаки форматирования вышеуказанный текст будет выглядеть вот так (рис. 9):
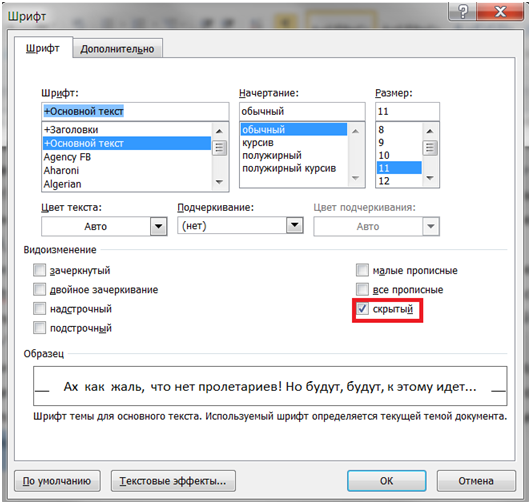
Скрытый текст не печатается. НО! Как же скрыть текст? Это очень просто 😉
Нажмите на «Скрытый» (рис. 11)
Зачем нам прятать текст? В первую очередь для настройки документа или шаблона текста, чтобы соответствовать специфическим требованиям. Вы также можете скрывать текст, если вы не хотите выводить его на печать в данный момент, но не хотите удалять.
Возвращаемся к знакам форматирования.
Якорь
Якорь представляет собой небольшую иконку в виде якоря корабля (рис. 12).
Конец ячейки
Установлено, что в ячейках данный знак означает собой конец последнего абзаца в ячейке или в ее конце. Она отражает форматирование ячейки (рис. 13).