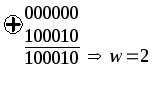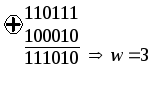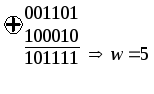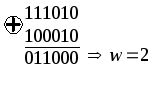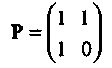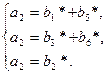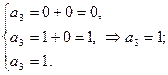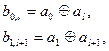кодирование и декодирование линейных кодов
1.4.2. Методы кодирования и декодирования линейных кодов
Правила кодирования линейного кода задает проверочная матрица.
Пусть матрица H определена следующим образом:
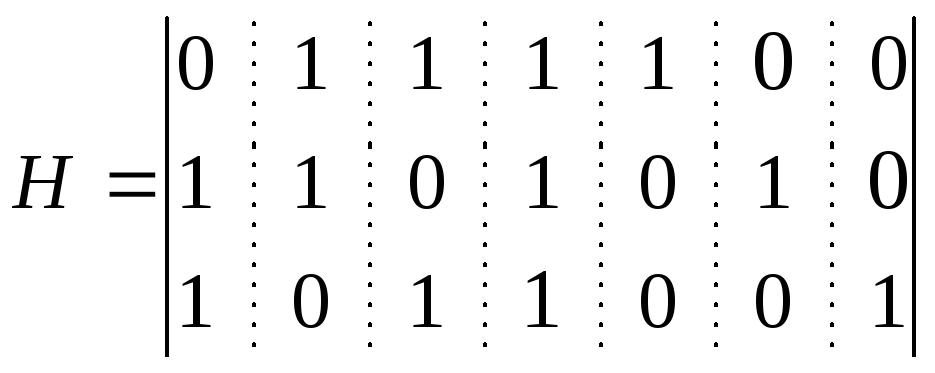
Матрица 
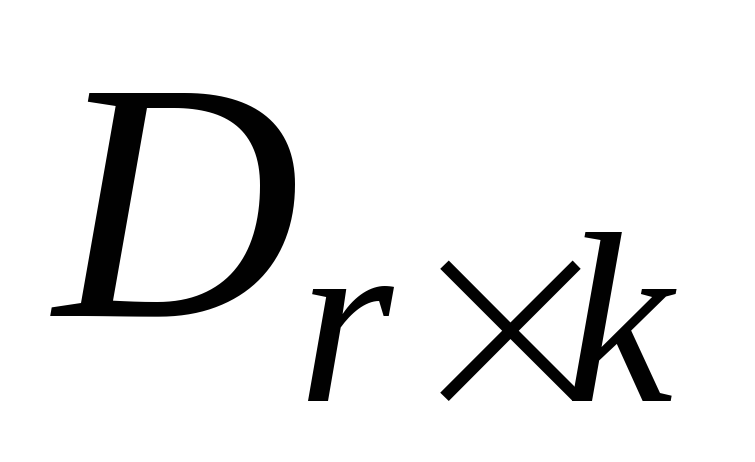
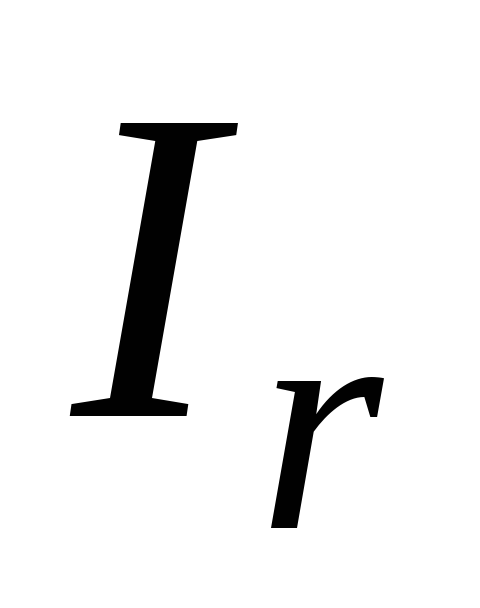
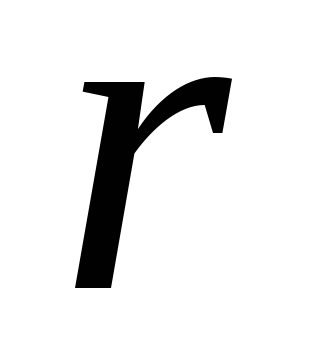
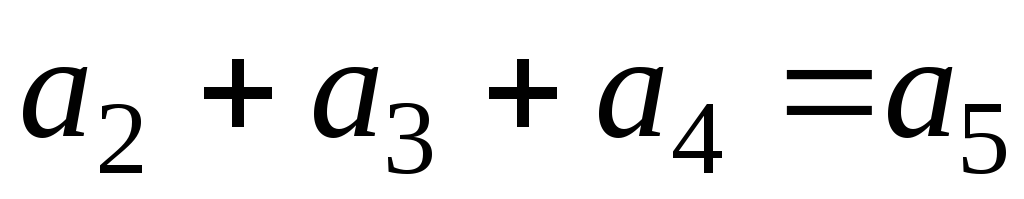
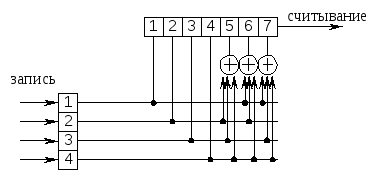
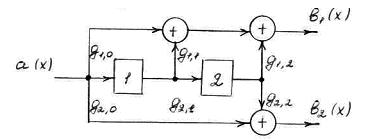
Структурная схема кодирующего устройства, задаваемого проверочной матрицей 
Алгоритм декодирования включает в себя вычисление и анализ синдрома 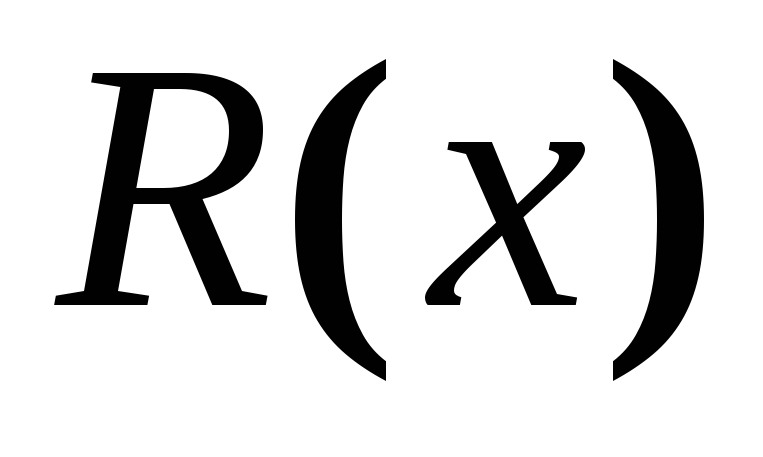
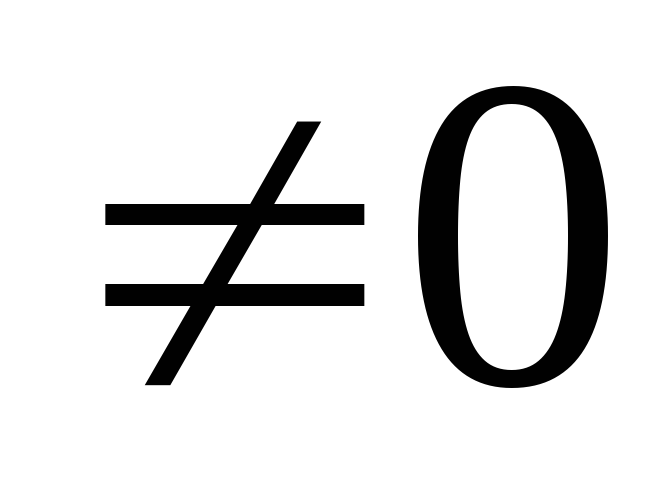
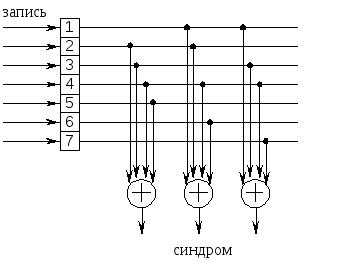
Структурная схема декодера, определенного проверочной матрицей (1.33), представлена на рис.1.10.
1.4.3. Методы кодирования и декодирования свёрточных кодов
При сверточном кодировании поток данных разбивается на блоки длины k0, которые называют кадрами информационных символов. Кадры информационных символов кодируются кадрами кодового слова длины n0 каждый. Причем кодирование каждого кадра информационных символов в отдельный кадр кодового слова производится с учетом предыдущих т кадров информационных символов.
Структура кодера определяется длиной регистра, числом сумматоров и связями каждого сумматора с регистром. Связи выражают двоичным числом (или порождающим полиномом). Единицы в разрядах числа указывают на наличие связей соответствующих отводов регистра с сумматором.
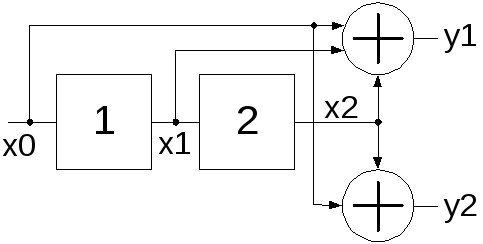
Например, приведенная на рис.1.11 схема кодера соответствует сверточному коду, определенному порождающими полиномами 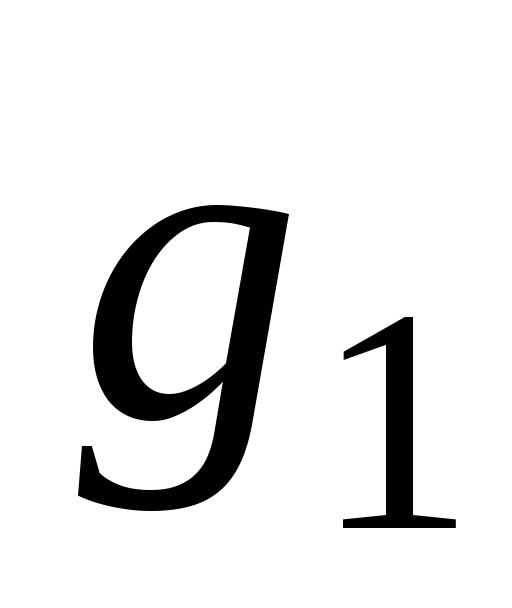
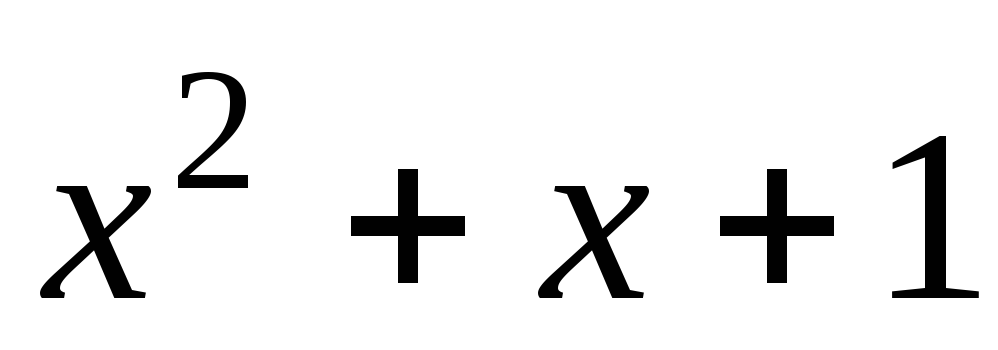
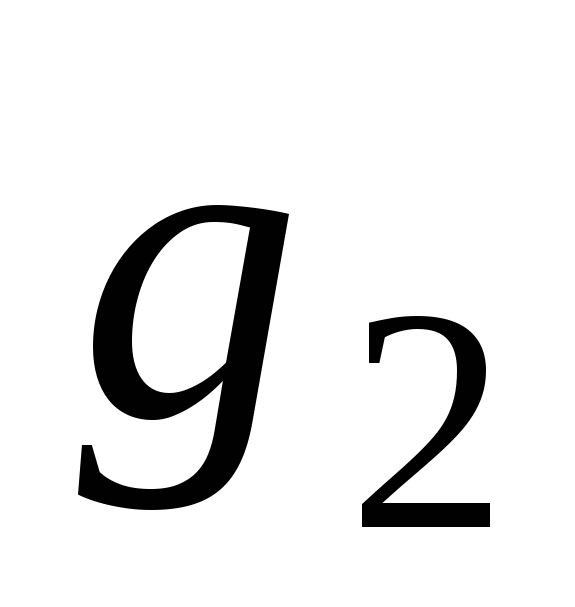
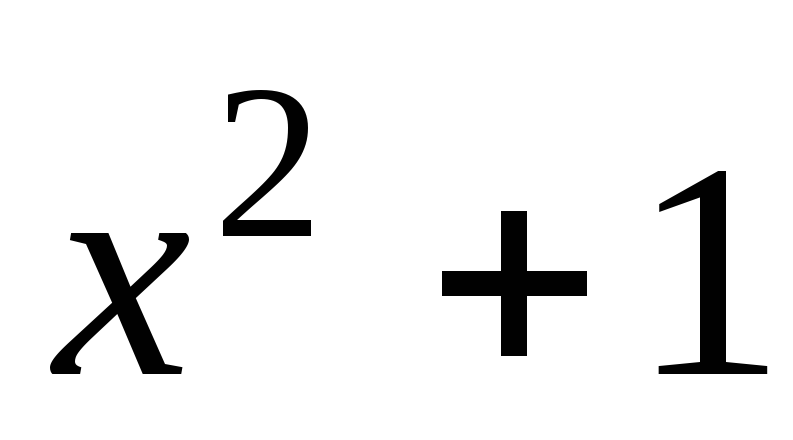
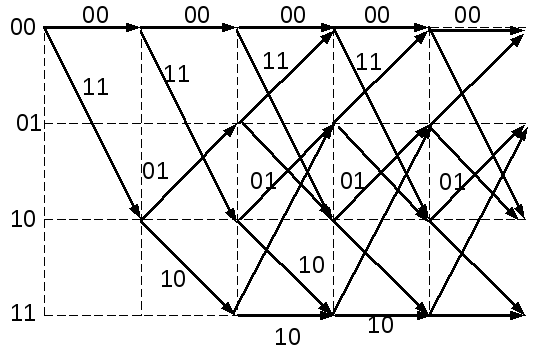
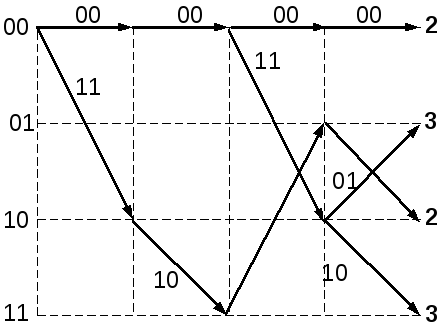
Способ представления связи между входными и выходными последовательностями называется решетчатой диаграммой (рис.1.12). Для решетчатой диаграммы характерны следующие утверждения:
состоит из узлов и ребер (ветвей);
число ребер, исходящих из узла, равно основанию кода;
выходные символы записываются над ветвями;
надписи около узлов характеризуют логическое состояние кодирующего устройства;
каждой информационной последовательности символов соответствует определенный путь на диаграмме;
процесс кодирования заключается в выборе одного из путей диаграммы.
Декодирование сверточных кодов осуществляется одним из трех методов: c вычислением проверочной последовательности, по принципу максимума правдоподобия или методом Витерби.
С вычислением проверочной последовательности. На приемной стороне из принятых информационных символов формируют проверочные по тому же закону, что и на передающей стороне, которые затем сравнивают с принимаемыми проверочными символами. Закон формирования проверочных символов выбирается таким образом, чтобы по структуре проверочной последовательности можно было определить искаженные символы. Метод применим только для систематических сверточных кодов.
Декодирование по принципу максимума правдоподобия сводится к задаче отождествления принятой последовательности с одной из 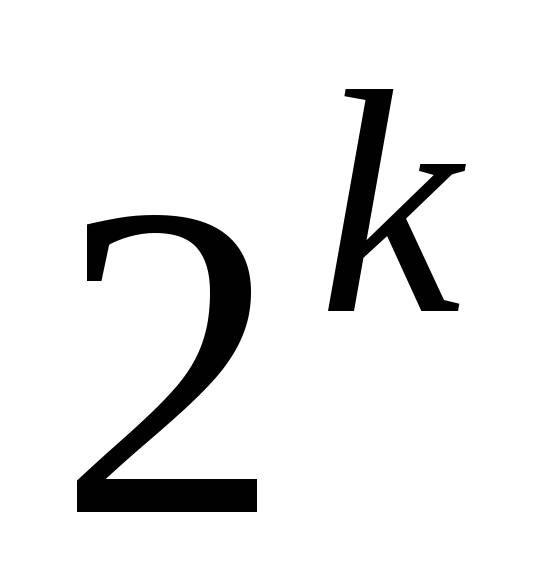
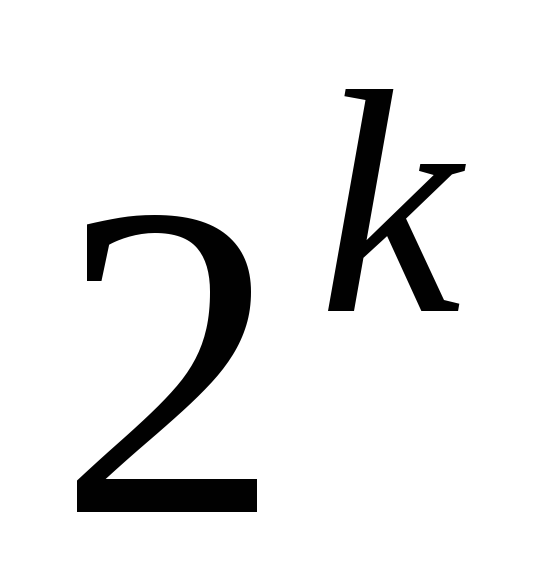
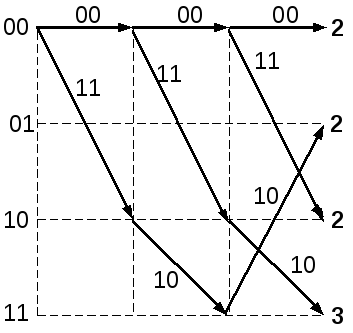
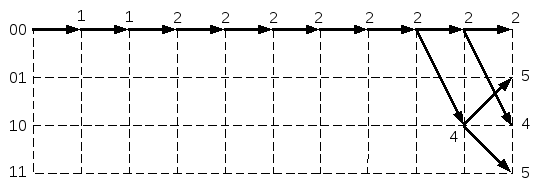
На третьем такте работы декодера (рис.1.13а) общее число путей равно 8. Декодер сравнивает метрики для пар путей, ведущих в каждый узел, и из каждой пары оставляет путь с меньшим весом:
Расчет веса пути для первого узла
Расчет веса пути для второго узла
Таким образом, для первого узла на диаграмме выбирается путь с весом 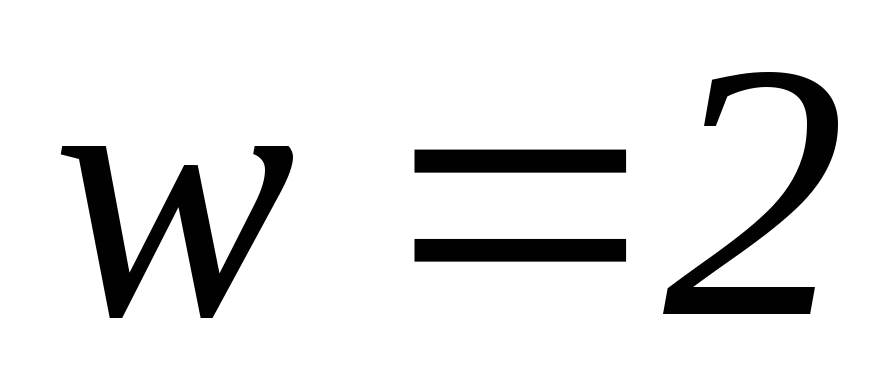
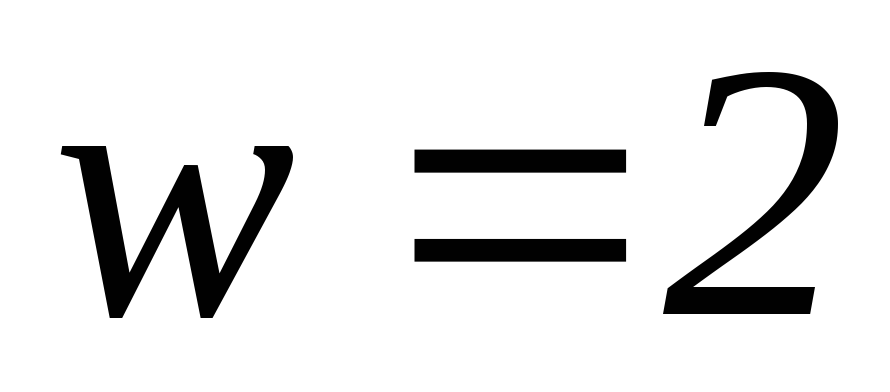

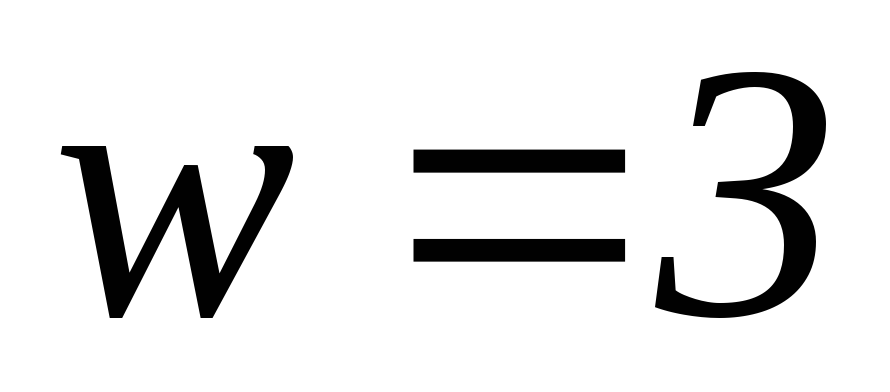
Глубина (число тактов), на которой происходит слияние путей, является случайной величиной, зависящей от ошибок в принятой последовательности, и заранее не может быть вычислена. Поэтому при практической реализации декодера устанавливают некоторую фиксированную глубину декодирования. В примере на 10-м такте первые восемь ветвей всех «выживших» путей совпадают (рис.1.13в). В этот момент согласно алгоритму Витерби, принимается решение о принятых символах.
1.3. Кодирование и декодирование линейных блоковых кодов
1.3.1. Кодирование с помощью матриц g и н
Равенство (1.10) определяет по существу правило кодирования для линейного блокового кода, которое может быть использовано непосредственно. Если кодирование должно быть систематическим, то произвольная порождающая матрица G линейного блокового (n, к, dmin) кода С может быть преобразована к систематической форме Gsys (иначе, к канонической форме) с помощью элементарных операций и перестановок столбцов матрицы. Матрица Gsys состоит из двух подматриц: k×k единичной матрицы, обозначаемой Ik, и k× (n-k) проверочной подматрицы Р. Таким образом,


Так как GH T = 0, то отсюда следует, что систематическая форма проверочной матрицы имеет вид

Пример 3. Рассмотрим двоичный линейный (4,2,2) код с порождающей матрицей
Перестановкой второго и четвертого столбцов преобразуем эту матрицу в систематическую форму
Таким образом, проверочная подматрица равна
В дальнейшем будет использовано обозначение u = (u0, u1,…,uk-1) для информационного сообщения и обозначение v = (v0, vl. vn-1) для соответствующего кодового слова кода С.
Если параметры С таковы, что k (n-k) или k/n > 1/2, тогда кодирование с помощью проверочной матрицы Н требует меньшего количества вычислений. Этот вариант кодирования основан на уравнении (1.12) (u, vp)H T = 0. Проверочные позиции (vk, vk+1, …, vn-1) вычисляются следующим образом:

Можно сказать, что элементами систематической формы проверочной матрицы являются коэффициенты проверочных уравнений, из которых вычисляются проверочные символы. Этот факт будет использован при обсуждении кодов с низкой плотностью проверок.
Пример 4. Рассмотрим двоичный линейный (4,2,2) код из примера 3. Пусть сообщение и кодовые слова обозначены u = (u0,u1) и v = (v0, v1, v2, v3), соответственно. Из уравнения (1.18) получаем
Соответствие между 2 2 = 4 двух битными сообщениями и кодовыми словами имеет следующий вид:
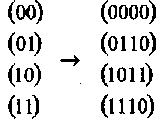
1.3.2. Декодирование по стандартной таблице
В этом разделе представлена процедура декодирования, которая находит кодовое слово v, ближайшее к принятому с искажениями слову r = v + е, где вектор ошибок е 
Рис. 5. Модель двоичного симметричного канала.
Стандартной таблицей (или стандартной расстановкой) для двоичного линейного (n, k, dmin) кода С называется таблица всех возможных принятых из канала векторов r, организованная таким образом, что может быть найдено ближайшее к r кодовое слово v.
Таблица 1. Стандартная таблица двоичного линейного блокового кода.
Стандартная таблица содержит 2 n — k строк и 2 к + 1 столбцов. Правые 2 к столбцов таблицы содержат все вектора из пространства V2= <0,1>n
Для описания процедуры декодирования необходимо ввести понятие синдрома. Определение синдрома произвольного слова из V2 следует из уравнения (1.12),

где Н проверочная матрица кода С. Покажем, что синдром является индикатором вектора ошибок. Предположим, что кодовое слово v 
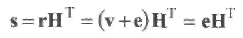
Таким образом, вычисление синдрома можно рассматривать как линейное преобразование вектора ошибок.
Процедура построения стандартной таблицы
Правые столбцы первой строки заполним кодовыми словами кода С, начиная с нулевого кодового слова. В первую ячейку первого столбца запишем нулевой синдром. Положим j = 0.
Для j =j + 1, найдем слово еj 
3. Повторяем шаг 2 процедуры, пока все вектора из V2 не окажутся включенными в таблицу. Эквивалентно, повторяем шаг 2 пока j п-к , иначе Стоп.
Пример 5. Стандартная таблица двоичного линейного (4,2,2) кода:
Декодирование с помощью стандартной таблицы выполняется следующим образом. Пусть r = v +е принятое слово. Найдем это слово в таблице и возьмем в качестве результата декодирования сообщение u, записанное в верхней (первой) ячейке того столбца, в котором лежит принятое слово r. По идее, этот процесс требует хранения в памяти всей таблицы и поиска в ней заданного слова.
Синдром всех элементов i-ой строки равен

и не зависит от конкретного значения кодового слова v 
и найти его в левом столбце стандартной таблице; взять лидер смежного класса еj из второго столбца той же строки и прибавить его к принятому слову, получив ближайшее к принятому r = е’j + v’ кодовое слово v’.
Пример 6. Снова рассмотрим двоичный линейный (4, 2, 2) код из Примера 3. Положим, что передано было кодовое слово (0110), а принято слово (0010). Тогда синдром равен
Находим в стандартной таблице лидер смежного класса (0100) и получаем декодированное кодовое слово (0010)+(0100)=(0110). Одиночная ошибка в слове исправлена! Это может показаться странным, так как минимальное кодовое расстояние равно 2 и, согласно условию (1.8), исправление однократных ошибок невозможно. Однако объяснение этому может быть найдено в стандартной таблице (Пример 5). Заметим, что третья строка таблицы содержит два различных двоичных вектора веса 1. Это означает, что только три из возможных четырех одиночных ошибок могут быть исправлены. В Примере 6 дана одна из исправляемых ошибок.
В случае систематического кодирования рассмотренная выше процедура находит оценку переданного сообщения на первых k позициях декодированного слова. Это может быть одной из возможных причин применения систематического кодирования.
ДЕКОДИРОВАНИЕ ЛИНЕЙНЫХ КОДОВ
Существует три основных метода декодирования линейных кодов:
— декодирование по максимуму правдоподобия (по минимуму расстояния);
— мажоритарное декодирование (по большинству проверок);
— декодирование по синдрому.
Декодирование по максимуму правдоподобия
В качестве переданного слова 

Рисунок 5.1 – Структурная схема декодера по минимуму расстояния.
На рисунке: УСр – устройство сравнения; ГКС – генератор кодовых слов; РУ – решающее устройство.
Данный метод используется, когда число информационных символов 
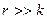
Мажоритарное декодирование
Основано на том, что каждый информационный символ можно выразить через другие символы кодового слова с помощью линейных соотношений. Окончательное решение о значении символа принимается по мажоритарному принципу (по большинству) результатов таких проверок.
Существует три способа построения систем проверочных уравнений для декодирования символа:
— системы с разделенными проверками – символ, относительно которого разделяется система, входит во все уравнения. Любой другой символ входит не более, чем в одно уравнение. Для коррекции 

— системы с 



— системы с квазиразделенными проверками – система разделима относительно некоторой суммы символов. На первом этапе она разрешается относительно суммы символов, а на втором – относительно конкретного символа.
Рисунок 5.2 – Структурная схема мажоритарного декодера.
На рисунке: 1…k – устройства, реализующие проверки для соответствующей системы; МЭ – мажоритарный элемент, принимающий решение о значении символа по большинству результатов проверок.
Код (8,4) задан матрицей:

Система уравнений по матрице Н:
Система проверочных уравнений для 
Система проверочных уравнений для 
Система проверочных уравнений для 
Система проверочных уравнений для 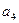
Пусть 

Результат декодирования: 
Декодирование по синдрому
Основано на стандартной таблице – таблице всех возможных принятых из канала слов, организованной таким образом, что может быть найдено ближайшее к принятому кодовое слово. Она содержит 

Таблица – Стандартная таблица.
| s1=(0…0) r | b1=(0…0) n | b2 | … | bM |
| s2 … sN | e2 … eN | b2+e2 … b2+eN | … … … | bM+e2 … bM+eN |
bi – кодовые слова;
ej – векторы ошибок – образцы ошибок минимального веса;
bi+ej – слова, не являющиеся кодовыми;
si=ei∙H T – синдромы – векторы размерностью r, указывающие на наличие и расположение ошибок в принятом слове.
1. Вычисляется синдром 


Если 



2. По 

3. Ближайшее к принятому кодовое слово 


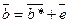
Рисунок 5.3 – Структурная схема декодера по синдрому.
На рисунке: Б – буфер хранения принятого слова; БВС – блок вычисления синдрома; С – селектор (дешифратор) синдрома; К – корректор.
Данный метод используется, когда число проверочных символов 
Пусть 
1. 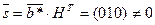
2. 
3. 
1. [3.1.2] с. 309…312, 317…318;
[3.1.5] с. 147.. 149, 150…151;
[3.1.14] с. 258…261, 271…273.
2. Код (7,4) задан порождающей матрицей:

Провести декодирование по синдрому принятого слова 
6 НЕПРЕРЫВНЫЕ (РЕКУРРЕНТНЫЕ) КОДЫ
Общие сведения
Непрерывные коды используют непрерывную обработку информации короткими фрагментами. Кодер для непрерывного кода обладает памятью, т.е. символы на его выходе зависят не только от очередного фрагмента информационных символов на входе, но и предыдущих символов на его входе и (или) выходе. Поэтому коды называются рекуррентными (recur – возвращаться, повторяться).
Эти коды применяют для обнаружения и исправления пакетов ошибок. Пакет ошибок – ошибка, затрагивающая цепочку символов. Описывается длиной 

Пакеты ошибок длиной 4 могут быть такими:
К непрерывным кодам относят цепной и сверточные. Цепной код является простейшим случаем сверточных.
Цепной код
В таком коде после каждого информационного символа следует проверочный. Закодированная последовательность имеет вид:
где 


Код позволяет исправить пачки ошибок длиной 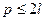

Сверточные коды (ск)
Это линейные, рекуррентные коды. Название обусловлено тем, что кодирование информации СК представляет собой операцию свертки двух функций:
где 
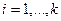



Набор порождающих полиномов определяет внутреннюю конструкцию кодера.
Рисунок 6.1 – Обобщенная структурная схема кодера СК.
Кодирующее устройство содержит 

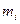



На практике чаще используются коды с единственным входным потоком ( 

Рисунок 6.2 – Структурная схема кодера несистематического СК с