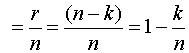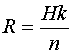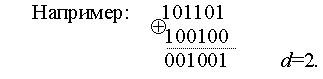кодовые комбинации кода максимальной длины содержат число единиц
Электронные средства сбора, обработки и отображения информации
Оглавление
Помехоустойчивое кодирование
Понятие корректирующего кода
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.
Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).
В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.
Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой букве сообщения соответствует блок из п символов.
Блоковый код называется равномерным, если п (значность) остается одинаковой для всех букв сообщения.
Различают разделимые и неразделимые блоковые коды.
При кодировании разделимыми кодами кодовые операции состоят из двух разделяющихся частей: информационной и проверочной. Информационные и проверочные разряды во всех кодовых комбинациях разделимого кода занимают одни и те же позиции.
При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.
Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.
Общие принципы использования избыточности
Способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. На ввод кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из п двоичных символов, причем n>k. Всего может быть 





— 
— 

— 


Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:
Кобн 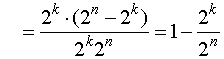
Рассмотрим, например, обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (п=k+1). Общее число выходных последовательностей составит 

Кобн 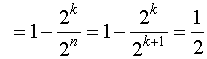
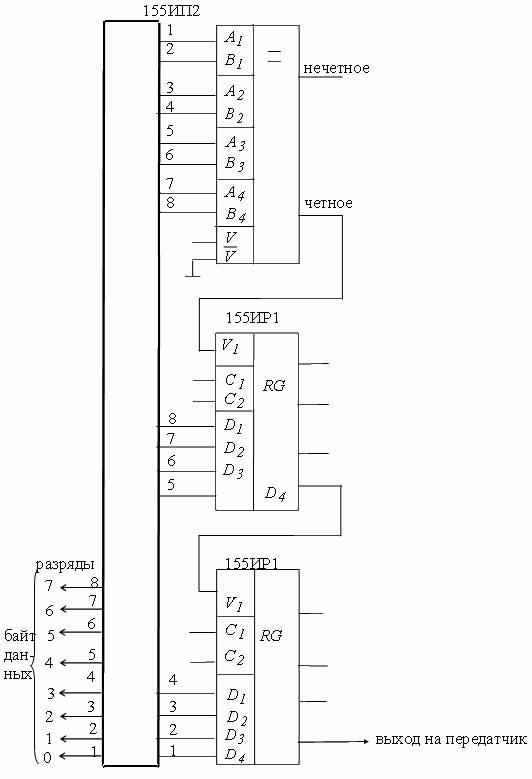
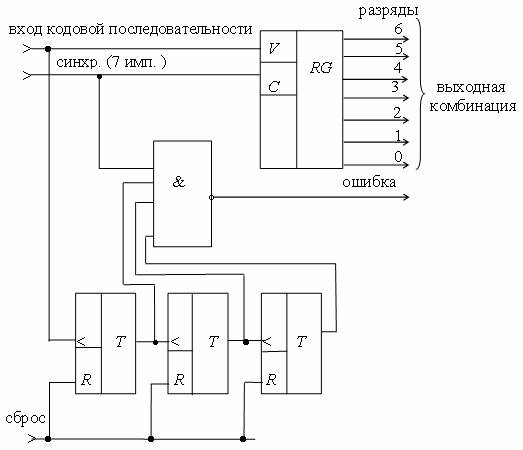
Пример кодирующего устройства с проверкой на четность показан на рис.
Основные параметры корректирующих кодов
Основными параметрами, характеризующими корректирующие свойства кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых или исправленных ошибок.
Рассмотрим суть этих параметров.
Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов
Относительной избыточностью корректирующего кода называют величину
отн
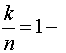
Эта величина показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы. Ее еще называют относительной скоростью передачи информации.
Если производительность источника равна Н символов в секунду, то скорость передачи после кодирования этой информации будет равна
поскольку в последовательности из п символов только k информационных.
Если число ошибок, которое нужно обнаружить или исправить, значительно, необходимо иметь код с большим числом проверочных символов. Скорость передачи информации при этом будет уменьшена, так как появляется временная задержка информации. Она тем больше, чем сложнее кодирование.
Кодовое расстояние характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом символов, которыми комбинации отличаются одна от другой.
Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2.
Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до п, равной значности кода.
Число обнаруживаемых ошибок определяется минимальным расстоянием 
В безызбыточном коде все комбинации являются разрешенными, 
Теорема. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух.
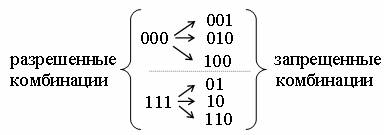
Доказательство. Возьмем значность кода п=3. Возможные комбинации натурального кода образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111. Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как 

Пусть подмножество разрешенных комбинаций образовано по принципу четности числа единиц. Тогда подмножества разрешенных и запрещенных комбинаций будут такие:
Очевидно, что искажение помехой одного разряда (одиночная ошибка) приводит к переходу комбинации в подмножество запрещенных комбинаций. То есть этот код обнаруживает все одиночные ошибки.
В общем случае при необходимости обнаруживать ошибки кратности 


В этом случае никакая ошибка кратности 
Ошибки можно не только обнаруживать, но и исправлять.
Теорема. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех.
Доказательство. Пусть, как и в предыдущем примере, п=3. Примем разрешенные комбинации 000 и 111 (кодовое расстояние между ними равно 3). Разрешенной комбинации 000 поставим в соответствие подмножество запрещенных комбинаций 001, 010, 100. Эти запрещенные комбинации образуются в результате возникновения единичной ошибки в комбинации 000.
Аналогично разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных комбинаций 110, 011, 101. Если сопоставить эти подмножества запрещенных комбинаций, то очевидно, что они не пересекаются:
В общем случае исправляемые ошибки кратности 


где 
Если, например, п=7, 
Нужно отметить, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала связи.
Групповой код с проверкой на четность
Недостатком кода с четным числом единиц является необнаружение четных групповых ошибок. Этого недостатка лишены коды с проверкой на четность, где комбинации разбиваются на части, из них формируется матрица, состоящая из некоторого числа строк и столбцов:
Строки образуются последовательно по мере поступления символов исходного кода. Затем после формирования т строк матрицы производится проверка на четность ее столбцов и образуются контрольные символы 
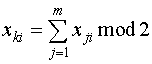
При таком кодировании четные групповые ошибки обнаруживаются. Не обнаруживаются лишь такие ошибки, при которых искажено четное число символов в столбце.
Можно повысить обнаруживающую способность кода путем одновременной проверки на четность по столбцам и строкам или столбцам и диагоналям (поперечная и диагональная проверка).
Если проверка проводится по строкам и столбцам, то код называется матричным.
Проверочные символы располагаются следующим образом:
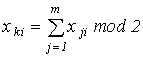
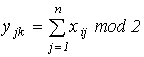
В этом случае не обнаруживаются только ошибки четной кратности с кратностью 4, 8, 16 и т.д., при которых происходит искажение символов с попарно одинаковыми индексами строк столбцов. Наименьшая избыточность кода получается в том случае, когда образуемая матрица является квадратной.
Недостатком такого кода является необходимость внесения задержки в передачу информации на время, необходимое для формирования матрицы.
Матричный код позволяет исправлять одиночные ошибки. Ошибочный элемент находится на пересечении строки и столбца, в которых имеется нарушение четности.
Коды с постоянным весом
Весом называется число единиц, содержащихся в кодовых комбинациях.
В коде «3 из 7» возможных комбинаций сто двадцать восемь (
Схема устройства определения веса комбинаций кода «3 из 7» приведена на рис. 2.6.
Циклические коды
Циклические коды характеризуются тем, что при циклической перестановке всех символов кодовой комбинации данного кода образуется другая кодовая комбинация этого же кода.


Например, комбинация 1001111 (п=7) будет представлена многочленом
При таком представлении действия над кодовыми комбинациями сводятся к действиям над многочленами. Эти действия производятся в соответствии с обычной алгебры, за исключением того, что приведение подобных членов осуществляется по модулю 2.
Обнаружение ошибок при помощи циклического кода обеспечивается тем, что в качестве разрешенных комбинаций выбираются такие, которые делятся без остатка на некоторый заранее выбранный полином G(x). Если принятая комбинация содержит искаженные символы, то деление на полином G(x) осуществляется с остатком. При этом формируется сигнал, свидетельствующий об ошибке. Полином G(x) называется образующим.
Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением подобных членов по модулю 2:
Таким образом, все полиномы, отображающие комбинации циклического кода, будут иметь степень ниже п.
Часто в качестве полинома, на который осуществляется деление, берется полином G(x)=
Большим преимуществом циклических кодов является простота построения кодирующих и декодирующих устройств, которые по своей структуре представляют регистры сдвига с обратными связями.
Число разрядов регистра выбирается равным степени образующего полинома.
Обратная связь осуществляется с выхода регистра на некоторые разряды через сумматоры, число которых выбирается на единицу меньше количества ненулевых членов образующего полинома. Сумматоры устанавливаются на входах тех разрядов регистра, которым соответствуют ненулевые члены образующего полинома.
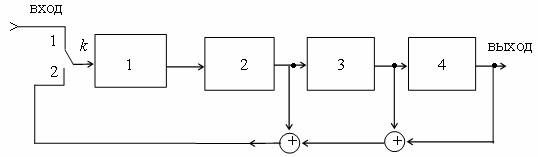
На рис. 2.7 приведена схема кодирующего регистра для преобразования четырехразрядной комбинации в семиразрядную.
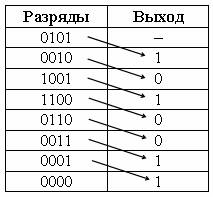
В табл. 2.3 показано, как путем сдвигов исходной комбинации 0101 получается комбинация циклического кода 1010011. п=7, k=4. Комбинация 0101, ключ в положении 1. В течение первых четырех тактов регистр будет заполнен, затем ключ переводится в положение 2. Обратная связь замыкается. Под действием семи сдвигающих тактов проходит формирование семиразрядного циклического кода.
Свойства циклического кода:
1) циклический код обнаруживает все одиночные ошибки, если образующий полином содержит более одного члена. Если G(x)=x+1, то код обнаруживает одиночные ошибки и все нечетные;
2) циклический код с G(x)=(x+1)G(x) обнаруживает все одиночные, двойные и тройные ошибки;
Кодовые комбинации кода максимальной длины содержат число единиц
Так, для передачи букв русского алфавита (их 32) необходимо передать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача одной из десяти цифр от 0 до 9 для каждого десятичного разряда. То есть для передачи букв русского алфавита нужно иметь техническую возможность передачи и приема десяти различных сигналов, соответствующих различным цифрам.
На практике при кодировании дискретных сообщений широко применяется двоичная система счисления.
6.1.2.2. Корректирующие коды
Говорят, что в канале произошла ошибка кратности q, если в кодовой комбинации q символов приняты ошибочно. Легко видеть, что кратность ошибки есть не что иное, как расстояние Хэмминга между переданной и принятой кодовыми комбинациями, или, иначе, вес вектора ошибки.
Рассматривая все разрешенные кодовые комбинации и определяя кодовые расстояния между каждой парой, можно найти наименьшее из них d = min d(i; j), где минимум берется по всем парам разрешенных комбинаций. Это минимальное кодовое расстояние является важным параметром кода. Очевидно, что для простого кода d=1.
Обнаруживающая способность кода характеризуется следующей теоремой. Если код имеет d>1 и используется декодирование по методу обнаружения ошибок, то все ошибки кратностью q ³ d, то одни из них обнаруживаются, а другие нет.
Таким образом, применение достаточно эффективных (а значит, и достаточно длинных) кодов при табличном методе кодирования и декодирования технически невозможно.
Поэтому основное направление теории помехоустойчивого кодирования заключается в поисках таких классов кодов, для которых кодирование и декодирование осуществляются не перебором таблицы, а с помощью некоторых регулярных правил, определенных алгебраической структурой кодовых комбинаций.
6.1.2.3. Линейные коды
Одним из таких классов являются линейные блоковые коды. Линейными называются такие двоичные коды, в которых множество всех разрешенных блоков является линейным пространством относительно операции поразрядного сложения по модулю 2.
Если записать k линейно-независимых блоков в виде k строк, то получится матрица размером n ´ k, которую называют порождающей или производящей матрицей кода G.
Множество линейных комбинаций образует линейное пространство, содержащее 2 k блоков, т.е. линейный код, содержащий 2 k блоков длиной n, обозначают (n, k). При заданных n и k существует много различных (n, k)-кодов с различными кодовыми расстояниями d, определяемых различными порождающими матрицами. Все они имеют избыточность e k =1-k/n или относительную скорость R k =k/n.
Преимуществом линейных, в частности систематических, кодов является то, что в кодере и декодере не нужно хранить большие таблицы всех кодовых комбинаций, а при декодировании не нужно производить большое количество сравнений.
Однако, для получения высокой верности связи следует применять коды достаточно большой длины. Применение систематического кода в общем случае, хотя и позволяет упростить декодирование по сравнению с табличным способом, все же при значениях n порядка нескольких десятков не решает задачу практической реализации.
6.1.2.4. Совершенные и квазисовершенные коды
Число известных совершенных кодов ограничено кодами Хэмминга значности и бинарным циклическим кодом Голея.
Класс квазисовершенных кодов значительно шире, чем класс плотно упакованных кодов.
Совершенные и квазисовершенные коды обеспечивают максимум вероятности правильного приема комбинации при равновероятных ошибках в канале связи.
6.1.2.5. Циклические коды
Рассмотрим данный класс кодов подробнее. Название циклических кодов связано с тем, что каждая кодовая комбинация, получаемая путем циклической перестановки символов, также принадлежит коду. Так, например, циклические перестановки комбинации 1000101 будут также кодовыми комбинациями 0001011, 0010110, 0101100 и т.д.
Представление кодовых комбинаций в виде многочленов F(x) позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2. Деление осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложения по модулю 2. Циклическая перестановка кодовой комбинации эквивалентна умножению полинома F(x) на x с заменой на единицу переменной со степенью, превышающую степень полинома.
Особую роль в теории циклических кодов играют неприводимые многочлены G(x), т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней.
Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x).
Делим полином Q(x)x r на порождающий полином G(x) степени r, при этом получаем частное от деления C(x) такой же степени, что и Q(x).
Полином F(x) делится без остатка на G(x), т.е. представляет собой разрешенную комбинацию циклического (n,k)-кода.
Таким образом, разрешенную кодовую комбинацию циклического кода можно получить двумя способами: умножением кодовой комбинации простого кода C(x) на полином G(x) или умножением кодовой комбинации Q(x) простого кода на одночлен x r и добавлением к этому произведению остатка R(x).
В первом случае информационные и проверочные разряды не отделены друг от друга (код получается неразделимым ). Во втором случае получается разделимый код. Этот код достаточно широко используется на практике, поскольку процесс декодирования и обнаружения ошибок при использовании разделимого кода выполняется проще.
Умножение Q(x) на x r эквивалентно повышению степени многочлена на r. Q(x) = ® 10111.
Формирование проверочной группы осуществляется в процессе деления Q(x)x r на G(x).
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | ||||
| 0 | 1 | 0 | 0 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | 1 | 1 | |||||||||
| 0 | 0 | 1 | 1 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 0 | 1 | 1 | 0 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 1 | 0 | 0 |
Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок.
Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью и будут рассмотрены ниже в подразделе 6.1.2.8.
6.1.2.6. Прочие классы кодов
Наряду с циклическими кодами на практике используются другие типы кодов, обладающие различными свойствами. Подробное рассмотрение классов кодов выходит за рамки настоящего курса, поэтому приведем только их краткую характеристику.
Если интервал между символами, входящими в одну комбинацию, сделать больше максимально возможной длины группы ошибок, то в пределах комбинации группирования ошибок не будет. Группа ошибок распределится в виде одиночных ошибок на группу комбинаций. Одиночные ошибки будут легко обнаружены (исправлены) декодером.
6.1.2.8. Системы с обратной связью
Нередко встречаются случаи, когда информация может передаваться не только от одного абонента к другому, но и в обратном направлении. В таких условиях появляется возможность использовать обратный поток информации для существенного повышения верности сообщений, переданных в прямом направлении. При этом не исключено, что по обоим каналам (прямому и обратному) в основном непосредственно передаются сообщения в двух направлениях («дуплексная связь») и только часть пропускной способности каждого из каналов используют для передачи дополнительных данных, предназначенных для повышения верности.
Возможны различные способы использования системы с обратной связью в дискретном канале. Обычно их подразделяют на два типа: системы с информационной обратной связью и системы с управляющей обратной связью.
Системами с информационной обратной связью (ИОС) называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения:
В системах с управляющей обратной связью (УОС) приемное устройство на основании анализа принятого сигнала само принимает решение о необходимости повторения, изменения способа передачи, временного перерыва связи и передает об этом указание передающему устройству. Возможны и смешанные методы использования обратной связи, когда в некоторых случаях решение принимается на приемном устройстве, а в других случаях на передающем устройстве на основании полученной по обратному каналу информации.