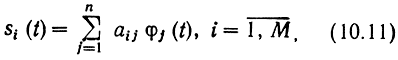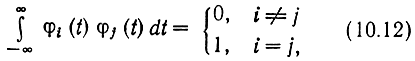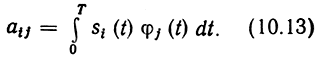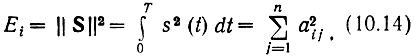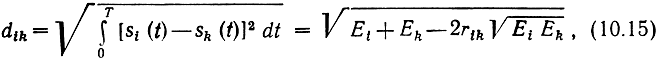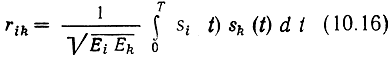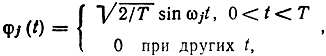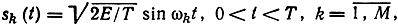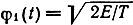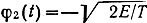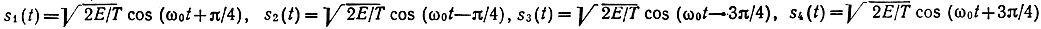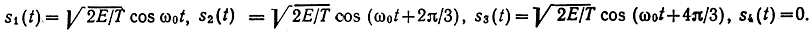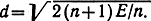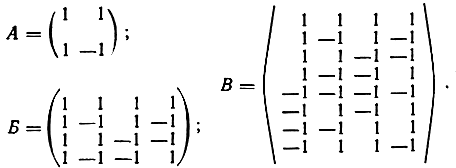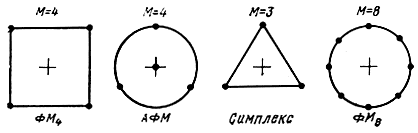коды подразделяются по величине позиционности на двухпозиционные и многопозиционные
Позиционный принцип в системах счисления.



Наиболее распространенными и совершенными являются позиционные системы счисления, т.е. системы, в которых значение каждой цифры в изображении числа зависит от ее положения (позиции) в ряду других чисел, изображающих число. Они обладают большим преимуществом наглядности и простотой выполнения арифметических операций.
Базис системы счисления – это последовательность так называемых ключевых чисел, каждое из которых задает значение цифры «по месту».
Число q называют основанием системы. Основанием системы является число, означающее количество символов, используемых в системе счисления. Это любое целое число не равное единице.
В десятичной системе счисления десять символов (цифр): 0,1,2,3,4,5,6,7,8,9;
В двоичной системе счисления два символа (цифры): 0,1;
Системы счисления, в которых веса смежных позиций цифр (разрядов) отличаются по величине в постоянное количество раз, равное основанию q системы счисления называются системы со степенными весами разрядов. Каждое число в таких системах может быть записано в цифровой и многочленной форме:
a – символы из алфавита системы счисления, целые числа меньше q;
Цифровую форму записи еще называют условно сокращенной формой записи числа в позиционной системе счисления, т.е. кодом числа.
Десятичная система счисления:
Двоичная система счисления:
Если десятичное число записать в двоичном виде, то оно в 3,3 раза больше содержит цифр, тем не менее именно двоичная форма записи используется в компьютере непосредственно для проведения различных вычислений.
Любой элемент, имеющий два устойчивых состояния, может использоваться для запоминания информации в компьютера.
Арифметические действия над одноразрядными двоичными числами выполняются по следующим правилам:
Дальше мы будем рассматривать позиционные системы счисления со степенными весами разрядов, в которых веса смежных позиций цифр (разрядов) отличаются по величине в постоянное количество раз, равное основанию q системы счисления.
Любое число в такой системе счисления может быть представлено в виде полинома разложения:
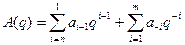
где: q – основание системы счисления,
n – количество цифр целой части числа,
m – количество цифр дробно части числа
Это же число с помощью этой формулы можно представить в виде разложения по степеням двойки.
В восьмеричной системе счисления алфавит состоит из восьми символов (цифр): 0, 1, … 7. Основание системы счисления q = 8. Для записи произвольного числа в восьмеричной системе счисления необходимо по формуле (1.1) найти его разложение по степеням восьмерки, а затем воспользоваться условно сокращенной записью.
Например, десятичное число 28(10) = 3×8 1 +4×8 0 = 34(8)
Шестнадцатеричная система. В этой системе алфавит включает в себя шестнадцать символов (цифр и букв): 0, 1, …, 9, A, B, C, D, E, F.
Например, число 75(10) = 4×16 1 + В×16 0 = 4В(16)
Наряду с двоичными кодами компьютере для ввода и вывода десятичных чисел используют специальное двоично-десятичное кодирование. При этом кодировании каждая десятичная цифра заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются в порядке следования десятичных цифр. При обратном преобразовании двоично-десятичный код разбивается на тетрады вправо и влево от запятой, отделяющей дробную и целую часть числа, которые затем заменяются десятичными цифрами.
Например, число 15,49(10) = 0001 0101,0100 1001(2-10)
Коды подразделяются по величине позиционности на двухпозиционные и многопозиционные
10.3. Многопозиционные сигналы и корректирующие коды
Ансамбль сигналов
Геометрически каждому сигналу ансамбля соответствует точка (или ректор) в n-мерном пространстве с координатами (ai1, ai2. ain i = 1. М. Энергия сигнала при этом равна квадрату
а расстояние между сигналами
— коэффициент взаимной корреляции рассматриваемых сигналов. В дальнейшем будем рассматривать ансамбли сигналов с одинаковыми энергиями Ei = Ek = E.
Наиболее распространенными многопозиционными сигналами являются ортогональные, биортогональные и симплексные. Если сигнальные точки выбрать на линиях, совпадающих с ортами φ на расстояниях √E от начала координат, то получим систему ортогональных сигналов. Число сигналов в таком ансамбле М = n. Так, если принять
Ортогональные сигналы образуют эквидистантную систему, расстояния между любыми двумя сигнальными точками которой одинаковы и, согласно выражению (10.15), равны d = √2E. Биортогональные сигналы образуются по следующему правилу: к каждому ортогональному сигналу добавляется противоположный. Здесь число сигналов М = 2n. Простейшим из биортогональных
является ансамбль с М = 4. Сигналы имеют одинаковые энергии и находятся на одинаковом расстоянии от начала координат. На (плоскости они образуют квадрат (рис. 10.4). При выборе в качестве базисных функций
Известные сигналы с амплитудно-фазовой модуляцией (АФМ) образуют круговую сеть (см. рис. 10.4): например, три сигнала равномерно распределены по окружности, а четвертый расположен в центре окружности. В том же базисе они могут быть представлены так:
Многопоэиционные сигналы с фазовой модуляцией (ФМ) образуют круговую сеть с равномерным распределением точек по окружности. Построить ансамбли ортогональных и биортогональных многопозиционных сигналов можно и на основе двоичных последовательностей. Для этого обычно используют элементарную матрицу Адамара А, повторением которой трижды в позитивной и один раз в негативной форме можно увеличить размеры матрицы каждый раз вдвое и получить матрицу Б, которая представляет ансамбль ортогональных сигналов с М = 4:
Каждая строка этой матрицы (последовательность двоичных символов) образует один сигнал. Нетрудно проверить, что эти строки (сигналы) взаимноортогональны. Дополняя матрицу Б инверсиями строк, получим матрицу В, представляющую ансамбль М = 8 биортогональных сигналов. Аналогично строятся ансамбли с большим числом сигналов М. Симплексные сигналы также могут быть получены на основе двоичных последовательностей [12].
Рис. 10.4. Примеры ансамблей двумерных сигналов
Помехоустойчивость систем связи в общем случае зависит как от вида передаваемых сигналов, так и от способа приема. При оптимальном приеме реализуется потенциальная помехоустойчивость. Алгоритм оптимального приема М-позиционных сигналов определяется системой неравенств (6.23), а вероятность ошибки вычисляется как вероятность невыполнения этих неравенств.
В § 6.5 получены выражения для вероятности ошибки при М = 2. Для не двоичных систем (М>2) получить такие простые выражения не всегда удается. Для некоторых ансамблей сигналов такие формулы имеются в [8], а для других, путем численного интегрирования, получены графики зависимости p = f(E/N0) [12, 18], которые ниже используются для вычисления энергетической эффективности р. Для приближенных вычислений при симметричных системах можно воспользоваться верхней оценкой (6.60)
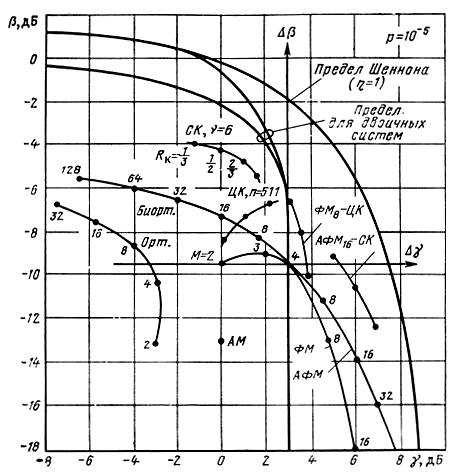
Различают два класса многопозиционных сигналов. Первый образуют «плотные» сигналы, когда с ростом объема ансамбля М при фиксированной размерности n расстояние между сигналами уменьшается, а удельная скорость γ, согласно (10.18) возрастает при соответствующем снижении энергетической эффективности β. В качестве примера таких сигналов на рис. 10.5 приведены кривые для многопозиционных сигналов ФМ и АФМ.
Рис. 10.5. Кривые энергетической и частотной эффективности систем с многопозиционными сигналами и корректирующими кодами
Приведенные на рис. 10.5 βγ-диаграммы позволяют количественно оценить обменный выигрыш (проигрыш) различных систем. Так, например, применение биортогональных сигналов с М = 16 позволяет получить энергетический выигрыш Др = 2,4 дБ в обмен на снижение удельной скорости γ в 2 раза (3 дБ). Обмен энергетической эффективности на частотную можно осуществить с помощью многопозиционных сигналов с ФМ. Однако более эффективными являются АФМ сигналы.
Расчетные кривые на рис. 10.5 показывают, что применение циклического кода в канале с ФМ или сверточного кода в канале с АФМ позволяет получить одновременно выигрыш как по энергетической, так и по частотной эффективности или во всяком случае выигрыш по одному показателю без ухудшения другого. Построение таких высокоэффективных систем (η>0,5) на основе сложных сигнально-кодовых конструкций ведет к неизбежному увеличению сложности системы. Не пропускная способность (предел Шеннона), а сложность является ограничивающим фактором при построении высокоэффективных систем. Задача состоит в том, чтобы построить систему удовлетворяющую высоким показателям эффективности, при минимальной (допустимой) сложности, а следовательно, и стоимости системы.
Корректирующие коды
Весьма важным направлением в системах защиты информации компьютерных технологий является обеспечение достоверности и целостности передачи информационных сигналов по каналам теледоступа в информационно-телекоммуникационных системах. Это направление связано с построением систем передачи информации на основе методов помехоустойчивого кодирования – корректирующих кодов с обнаружением и исправлением ошибок, возникающих за счет случайного или преднамеренного воздействия помех в каналах теледоступа к вычислительным ресурсам.
Формируемые передающими устройствами кодовые комбинации, являющиеся носителями информации, при передаче по каналам связи от источника сообщений к приемнику могут подвергаться искажениям за счет воздействия на них различного рода помех (флуктуационных, импульсных, сосредоточенных по спектру или (и) по времени). При воздействии таких помех на кодовые комбинации искажениям подвергаются отдельные их элементы. В результате такого случайного воздействия элементы кодовых комбинаций могут переходить из состояния 1 в 0 и наоборот. При изменении только одного элемента кодовой комбинации это искажение называется одиночным искажением (D=1). Если переходные искажения 1 ® 0 или 0 ® 1 происходит в двух элементах кодовых комбинаций, то они называются двойным искажением (D = 2) и т.д.
В цифровых системах передачи данных для борьбы с помехами применяют корректирующие коды, обладающие определенной избыточностью, что позволяет специальным устройствам приемной аппаратуры (синдромам) анализировать принимаемые кодовые комбинации, обнаруживать и исправлять искажения, возникающие за счет воздействия помех. Такие коды относятся к классу помехоустойчивых кодов, их построение основывается на выборе из всех N=2 n комбинаций кода с n элементами некоторого подмножества кодовых комбинаций Np Ì N(Np
Позиционные и непозиционные системы счисления



Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
Например, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления – система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. В каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 | |
| Троичная | 0,1,2 | |
| Четвертичная | 0,1,2,3 | |
| Пятиричная | 0,1,2,3,4 | |
| Восьмиричная | 0,1,2,3,4,5,6,7 | |
| Десятиричная | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В | |
| Шестнадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В,D,E,F |
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 10 2 + 4 * 10 1 + 6 * 10 0
В нашем числе три цифры. Старшая цифра «2» имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра «4» имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
12310 = 1 * 10 2 + 2 * 10 1 + 3 * 10 0 ;
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х8 2 + 2 х 8 1 + 3 х 8 0 = 8310;
1012 = 1 х 2 2 + 0 х 2 1 + 1 х 2 0 = 510;
1Е316 = 1 х 16 2 + 14 х 16 1 + 3 х 16 0 = 48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (т.е. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа могут быть представлены следующим образом:
Таким образом, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
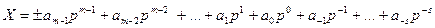
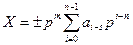
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n = m + s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (т.е. должен принадлежать множеству <0,1, p-1>).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число может быть представлено в виде последовательности нулей и единиц.
110100102 = 1 * 2 7 + 1 * 2 6 + 0 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 1 * 2 1 + 0 * 2 0 = 16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
2428 = 2 * 8 2 + 4 * 8 1 + 2 * 8 0 = 16210
В шестнадцатеричной системе допустимыми символами являются 0, 1, 9, A, B, C, D, E, F.
A216 = 10 * 16 1 + 2 * 16 0 = 16210
Коды подразделяются по величине позиционности на двухпозиционные и многопозиционные
Математика счетной логики
Любая предлагаемая система математической логики должна опираться на математику. Только, какую? Д. Буль разрабатывая свою математическую логику вкладывал в нее одну математику, а какая в ней заложена сейчас?
Математика логики не очень зависит от конкретного технического исполнения логических схем, синхронности проведения операций и других технологических факторов. В это смысле она абстрактна.
В статье [2] изложены самые первые логические обоснования предлагаемой системы без математических основ. На тот момент математики предлагаемой мною логики еще не было. Были какие-то мозаичные соображения.
Только сейчас, наконец-то, сформировалась какая-то система. Она и сейчас еще находится в процессе развития. Но, начало математики появилось.
В этой работе изложена математика основных логических операций. В некоторых моментах она повторяет и дополняет материал, изложенный в статье [2].
Получился какой-то симбиоз Булевой логики, и … многозначной надстройки.
Мне и самому пока не очень понятно, куда это приведет…
Логические и математические основы.
Сформулируем начальные правила формирования системы счетной логики:
Логическое пространство.
Что это такое – логическое пространство?
Это место, где решаются логические задачи. И средства, применяемые для их решения. Электронные схемы и программы. А, в общем, и то, и другое, и третье… — все, что необходимо для получения решения. Многоплановое понятие, включающее много компонентов.
Логическое пространство объединяет задача.
Для ее решения необходимы:
Вроде бы все основное есть. С этого начинается логическое пространство. Пока понятий и связей мало, все, кажется просто. Сложности появляются по мере развития. Тут все взаимосвязано. Новые цели требуют решения новых задач по их достижению, это требует увеличения количества понятий и связей, их систематизации и запоминания. Для этого нужно увеличение пространства хранения и проведения решений. И пошло, поехало…, и, кажется, нет этому конца.
Но, бесконечность развития призрачна. Все, хоть чем-то, но ограничено. И ограничения начинают препятствовать росту. В результате, ограниченным оказывается все. Пространство, время, память,… а решать задачи надо. Жизнь требует. Цели множатся. И задачи становятся все сложнее. Для их решения необходимо постоянно наращивать логическое пространство.
В ход идут все средства. Понятия и их связи все больше формализуются и систематизируются. Прошлые решения, хранящиеся в памяти, перепроверяются и переоцениваются, также систематизируются и группируются. Надо экономить пространство памяти. И саму память неплохо бы организовать и систематизировать, это позволяет сэкономить время на поиск.
О технической стороне этого пространства думать приходится постоянно. Все это логическое пространство функционирует на основе вполне конкретных конструкций. И не важно, «железо» это или живые клетки, это материальное воплощение механизма логики. Механизм требует материалов для строительства и поддержания его работоспособности, необходимой модернизации и развития. И места для его размещения. Реального физического объема.
Решение внутренних проблем поддержания, модернизации и дальнейшего расширения внутреннего логического пространства становится постоянной задачей для размещаемой в этом пространстве логической системы. В какой-то момент сложность и важность внутренних задач становится сопоставимой с внешними.
Этот момент наступает когда-нибудь при любой системе организации логического пространства. Рано или поздно. Но, лучше бы поздно. И чем позднее он наступит, тем лучше. Логическая система успеет развиться до более высокого уровня.
Вот когда проявляются стратегические начальные принципы организации системы, те, что мы заложили в самом начале ее развития.
Бинарная запись.
Как мне кажется, самым главным событием в области машинной математики 20 века было применение в системах автоматических вычислений бинарной записи. Несмотря на все остальные выдающиеся достижения.
Это событие стало началом нового пути развития вычислительной техники. Бинарная запись закрепила применение двоичной системы в качестве основной в системах автоматических вычислений. Я не знаю, что было вначале, доработка Булевой логики под систему бинарной записи с целью совмещения ее основ с двоичной системой счисления или события разворачивались в другом порядке, но победу одержала бинарная запись. Она стала нерушимым основанием вычислительной техники.
Вдруг оказалось, что бинарная форма записи числа имеет очень мощную философскую аргументацию. Настолько мощную, что не смотря на обнаруженные недостатки двоичной системы и Булевой логики все попытки отказаться от бинарной записи стали очевидно напрасными.
Бинарная запись, это предельная простота числа. Не надо определять количество разрядных единиц в разряде, достаточно просто зафиксировать, что там что-то есть. Это замена счета простой регистрацией изменения состояния разряда. Вычисления совместились с логическими операциями. На уровне граничных условий — 0 и 1.
Да, в каком-то смысле, это противоположные значения, отражающие состояние разряда. Это понимание сразу связало бинарную запись с философским пониманием дилеммы выбора противоположностей: ДА – НЕТ, правда – ложь, тепло — холодно, верх – низ, вперед – назад, … и т.д. Список бесконечен.
Бинарная запись из всех рациональных систем счисления возможна только в двоичной системе. Все остальные системы с любым рациональным основанием требуют отказа от бинарной записи.
Даже введение счетного значения (-1), это уже третье состояние разряда, а значит и отказ от бинарной записи. И любые аргументы в пользу троичной и любой другой счетной системы для принятия ее в качестве основной в системах автоматических вычислений рассыпаются в прах. Бинарная запись побеждает. Именно она, а не двоичная система.
Каждый, кто обнаруживает те или иные недостатки в двоичной системе, старается найти и «противоядие» в виде другой счетной системы. И, кажется, что надо только получше объяснить достоинства найденной системы, и все поймут, что двоичную систему просто необходимо срочно менять. Надо только объяснить и надежно аргументировать, и поймут,… но их почему-то упорно не понимают. Уже полвека.
Мне кажется, что в этом «виновата» бинарная запись. Все и всё понимают, но … отказаться от простоты и очевидности бинарной записи, начать все сначала, ради чего? Чтобы вместо одних уже известных недостатков одной системы получить новые неизвестные пока недостатки другой? Срабатывает правило: Бесплатный сыр – только в мышеловке. Зачем рисковать? Проще, чем есть, все равно уже не придумаешь. А все усложнения оборачиваются когда-нибудь новыми проблемами.
Под надежной защитой бинарной записи оказалась неуязвимой двоичная система счисления. И Булева логика, не самая логичная — тоже.
Но, попытки сломить сопротивление бинарной записи продолжаются с завидным упорством и постоянством.
Со стороны математической логики все сложнее. Логический аппарат математической логики растет. Он давно вырос из бинарной записи. И вроде бы, еще шаг, и … придет, наконец, многозначная логика. Все давно готовы к ее появлению.
Нет, бинарная запись и здесь пока прочно удерживает свои позиции. Булева логика практически «слилась» с двоичной математикой. И союз этот пока нерушим.
В связи с этим у меня уже достаточно давно зародилось сомнение в необходимости борьбы с бинарной записью. Пусть будет. Я стал внимательно присматриваться к ее сегодняшнему применению. В ней много хорошего, может быть только, слишком уж формально и ограниченно мы ее применяем, а так, больше и нет недостатков…
И двоичная система, это вполне удобная рациональная система, легкая и доступная. Позволяет проводить все математические действия в обычном порядке, не требует особенного подхода, и предельно проста в отображении и формировании чисел. Видимо, вопрос не в системе, а в направленности ее применения. Для вычислений она годится не хуже остальных. Хранить и передавать – не очень, но можно для этих целей какую-то иррациональную систему приспособить. Оставив при этом для чисел бинарную запись. Просто и надежно.
Нет, не так просто, и не надежно. В составе одного компьютера это — бесконечные преобразования. Для однопроцессорного аппарата – роскошь, кажется, неоправданная. А вот, для многопроцессорных систем – почему бы и нет?
Но, это для вычислительной техники, а для логики, применяемой в этой технике, такого компромисса пока не нашлось. Тут, как мне кажется, все же что-то надо менять…
Основы классических систем математической логики.
Булева логика.
Булева логика имеет два логических состояния: 0(НЕТ); 1(ДА).
Единицей информации является бит, имеющий одно знакоместо для отображения логического состояния, и системный байт, состоящий из 4 битов. Байт, как системный идентификатор адреса или операции еще сохраняет свое значение, а вот бит уже давно стал только единицей измерения информации, содержащейся в машинном слове. Длина этого слова все время увеличивается. Еще недавно она приближалась к 128 битам, но, сегодня и 256 бит или 64 байта в слове уже не предел.
Булева логика стала первичной основой вычислительной техники, в силу своего «ключевого» характера. В ее основе был выключатель. Включено – выключено, и ничего другого. Выключатель или замыкает цепь, или размыкает. Полярность питания значения не имеет. Цифры 0 и 1 подходят для фиксации этих состояний как нельзя лучше.
Троичная логика.
Троичная логика вынуждена учитывать не только состояние цепи, но и полярность питания. Иначе трех различных состояний не получить. В основе троичной логики – переключатель. Вверх, вниз, и нейтральное, среднее положение.
К моменту начала применения троичной логики техника уже стала широко использовать ключевой режим Булевой логики и других вариантов даже не пыталась применить. Потребовалось достаточно много времени для разработки своей технической базы и время было упущено, несмотря на, кажется, очевидные преимущества троичной логики по сравнению с Булевой. Но, очевидны ли преимущества?
Они бесспорны в отношении потенциального развития, как аппарата самой математической логики, так и применения ее для математических вычислений. Но, вот с технической стороны это не так очевидно. Второй источник питания, разнополярные импульсы и особая электронная техника для их обработки резко усложняют задачу применения троичной логики.
В этом случае надо поменять не только технику, но, и людей, привыкших к этой логике, и философию, и большую часть программных наработок, и т.д. и т.п. Полвека назад троичная логика, при всех ее достоинствах, сражение проиграла. Но и Булева логика с того времени лучше не стала. Сейчас для Булевой логики ситуация еще более драматична. Ее недостатки проявились во всей красе.
Но, несмотря ни на что, Булева логика продолжает пока удерживать монополию в цифровой технике. Сегодня ей все труднее сохранять свои позиции.
Сейчас в цифровой технике уже происходит определенное разделение труда. Компьютерные системы уже так разошлись в разных направлениях применения, что стали отдельными и узко специализированными системами. По архитектуре, применяемой технической базе, программному обеспечению это уже разные устройства, объединенные только каналами передачи информации с общими стандартами. И двоичной системой счета, да Булевой логикой.
Возможно, что и настал момент истины для Компьютера?
И снова нужен выбор основ для дальнейшего развития. На горизонте все чаще маячит троичная логика. Она уже не кажется невозможным решением сегодняшних проблем цифровой техники.
«…Рассмотрено два варианта построения троичных элементов:
· Двухпроводный с электрическими сигналами двух уровней (Е, 0) и кодированием троичных значений, например 01 – «+1», 00 – «0» и 10 – «-1». Четвертое состояние «11» либо блокируется, либо используется в целях обеспечения безопасности или достоверности информации – этой проблемой заинтересовался академик Амербаев В.М., математик. « [7]
Вот почему автор этой цитаты Д.Б.Малашевич рассматривает и другой вариант использования троичной логики. Так как в построении логических элементах используется Булева логика, то почему бы и не принять, что в трите два знакоместа. Это необходимо для отображения всех логических состояний в неотрицательном виде.
Очень близко к рассматриваемому вопросу, надо с к азать…
Возможно ли объединение систем?
Давайте, рассмотрим логическую систему с минимально допустимым количеством логических состояний и максимально возможным количеством логических ответов на уровне регистрации предельных граничных состояний. Т.е. четко различимых на уровне пороговой регистрации наличия или отсутствия этого ответа.
Минимально возможное количество логических состояний на уровне пороговой регистрации с технической стороны ограничивает количество источников питания и, соответственно, регистрируемых потенциалов до одного. Это требование и обеспечивает Булева логика.
А сколько логических ответов, вообще, можно получить при этих ограничениях?
Если информационный импульс опережает – (+), отстает – (-), совпадает — |1|, отсутствует – (0). Полярность импульса значения не имеет, так как мы ограничены одним источником питания и, соответственно одним потенциалом для регистрации. Все состояния технически четко различимы.
В глобальности логических состояний такой ключевой режим регистрации должен соблюдаться.
Пассивное логическое состояние – 0.
Активное логическое состояние – наличие информационного импульса в пункте приема.
(+);(-);1; — варианты логических ответов в пределах активного состояния.
Возможно ли объединение Булевой и троичной логики в какую-то подобную единую систему?
Этот вопрос возник у меня, когда я, в который уж раз смотрел на математические эквиваленты записи логических состояний Булевой и троичной логики. Уж очень близко их обозначения и исходят они от одного и того же – потенциала источника питания…
Это странно, но, если мы объедим логические состояния Булевой и троичной логики, то получим точно такую же логическую систему. У них много общего.
0,1,-1,+1, если состояние 0 одинаково.
Где-то мы уже видели нечто подобное, … не правда ли? Только с другими условиями фиксации. В данном случае мы уже не говорим о времени, фазах и синхронизации, мы говорим о формальных различиях для математической интерпретации. Есть формально различимые логические состояния. Чем они различаются, мы постараемся понять позже. Пока мы лишь отметим совпадение технических характеристик пороговой фиксации фазы информационного импульса и результата объединения логических систем Булевой и троичной логики.
Теперь попробуем дать первое объяснение каждому состоянию с новых позиций.
0 – состояние отсутствия информационного потенциала.
|1| – наличие информационного потенциала любой полярности.
-1 – наличие информационного потенциала (-) полярности.
+1 – наличие информационного потенциала (+) полярности.
В них можно выделить начальное состояние ожидания действий (0). И три активных единичных состояния. Мы можем дать им значения соответствующих логических ответов: ДА, НЕТ, и НЕ ЗНАЮ.
Если все логические состояния, как это понимается сегодня, имеют статус глобальной величины, то с технической стороны состояние |1| имеет двойственное понимание. Или мы принимаем импульс любой полярности, или – сразу двух, чтобы отличить его от однополярных импульсов. Если любой, то, как он будет отличаться от остальных активных состояний? А если сразу двухполярный импульс, то это – как?
Двухполяный импульс технически возможен. Было бы, чем его регистрировать. Это импульс от дифференцирующей цепи. Прямоугольный импульс, проходя через такую цепь, теряет постоянную составляющую наполнения импульса и превращается в две серии остроконечных импульсов. Причем, первая пара импульсов каждой из серий часто превышает по амплитуде напряжение питания и составляет разнополярную пару с резким перепадом потенциала. При этом полярность первого импульса в серии зависит от перепада потенциала начального прямоугольного импульса. От начала прямоугольного импульса получается одна полярность первого в серии выходных импульсов, от окончания – другая. Остальные импульсы серии имеют существенно меньшую затухающую амплитуду.
Это реактивная составляющая прямоугольного импульса, выделяемая на дифференцирующей цепи. Её, то применяют, то борются с ней, как с помехой в работе устройства.
Так что, вариант возможен. И зарегистрировать такой импульс или перепад потенциалов технической трудности не представляет. Только, может быть, не совсем это удобно. А вот получать разнополярные информационные импульсы таким способом – вполне. Но, при этом сразу возникают проблемы с синхронизацией работы схемы, и еще масса других вопросов.
Это уже пройденный не единожды этап, ведущий пока – в Н икуда.
Как я уже говорил, логический ответ имеет, в основном, локальное значение. Как Результат в Ответе логической операции. И лучше рассматривать его как локальную переменную в Результате.
Результат.
Давайте вспомним формулу:
Выражение 

В этой формуле Результат, величина, соотносящаяся и с Эквивалентом, и
с Выражением, так как они имеют взаимную эквивалентность. Как на рис.1.
Рис..1. Схема связей Результат – ответ – решение.
Эквивалент в нашей формуле, это логический Ответ, получаемый из логического Выражения — Решения задачи.
Решение 

Таким образом, Результатом Решения логической задачи становится один из Эквивалентов – Ответов задачи.
Перепишем формулу еще раз в сокращенном виде:
Решение 

Теперь рассмотрим данное выражение через создание пар противоположностей.
Решение 
Э 
Отметим, что, в общем случае, противоположность не является отрицательной величиной, а противоположной. Для продолжения рассмотрения вопроса нам придется принять такое равенство:
Р = | 
Величина равна своей противоположности, взятой по абсолютной величине.
Решение
2. Решение 
Для равенства: Решение = Р , наличие равносильности Решения и Результата может быть только в одном случае: Решение существует и его Ответ является Результатом этого Решения.
Для выражения Решение 

Решение =
Для равенства 
Действительным Результатом задачи является отсутствие Решения.
Заметим при этом, что отсутствие Решения эквивалентно отсутствию Ответа.
Для равенства Решение = 
Действительным Решением может считаться только вариант отсутствия Результата.
Так как вариантом Результата может быть любой Ответ, то отсутствие Результата означает отсутствие любого логического Ответа, принятого в системе.
При этих условиях для логической системы оба равенства можно объединить в систему справедливых равенств только в одном случае:
Где 0 может интерпретироваться только как отсутствие Ответа в Результате или — Ожидание Результата. Включим этот вывод в формулу эквивалентности Результата:
При такой интерпретации равенств (10) состояние 0 является одним из логических состояний, выражающее ожидание Ответа.
Теперь возьмем вторую пару эквивалентов из (5):
Э 
Ее также можно рассмотреть с позиций противоположностей:
2. Э 
Первое равенство можно рассматривать, как утверждение, что любой логический Ответ является Результатом решения.
Неравенство утверждает, что, если состояние Э не может быть Результатом решения, но существует в системе в качестве эквивалента, то оно не является Ответом.
Неравенство можно преобразовать в равенство через введение противоположности:


Одновременное выполнение этих равенств возможно только в случае:
Это и означает, что, состояние 0 не является ни Ответом системы, ни ее Результатом, являясь при этом одним из логических состояний системы.
Нам осталось рассмотреть эквивалентность:
Решение 
Это несколько вариантов перехода к математическим равенствам:
2. 
3. | 

4. 
5. Э =
Первое равенство утверждает, при действительности Решения все Эквиваленты Ответа существуют и равенство сохраняется.
Второе равенство утверждает, что при переходе Решения в свою противоположность в качестве эквивалента может существовать только противоположность Эквивалента Ответа. Их отсутствие.
Третье равенство устанавливает одинаковый математический вес противоположностей.
Четвертое равенство утверждает, что действительное решение может привести к противоположности Ответа — отсутствию Ответа. И эквивалентность, и равенство при этом сохраняются.
Последнее равенство утверждает, что Эквивалент будет существовать при отсутствии Решения.
В этих утверждениях есть несколько противоречий. Для разрешения этих противоречий необходимо перегруппировать равенства:
1.
3.
5. | 

В первой группе равенств при выполнении условия, что Э = Ответ возможно только одно общее решение:
При равносильности всех логических ответов системы и одном математическом весе всех ответов равном 1 равенства существуют.
Вторая группа равенств дает также единственное решение для существования системы равенств:
Такое решение системы равен ств пр иводит к равенству сравниваемых величин и их противоположностей. Это возможно только при отсутствии и того и другого.
0 противоположности не имеет. Мы уже находили это решение.
Логическое состояние 0 может существовать в процессе Решения, но Ответом не является. Эквивалент 0, вместо логического Ответа, может существовать, но Результатом не является. 0 — это устойчивое логическое состояние системы, не являющееся Ответом системы.
Локальные ответы и глобальные логические состояния.
Как мы уже выяснили логические состояния – основа любой базовой компьютерной логики, это электрические потенциалы примененных источников питания, появляющиеся в установившихся режимах на выходах электронных логических элементов. Как их не обозначай и не называй. В Булевой логике таких состояний — два, в троичной – три.
Как называется состояние, которое возникает сразу после включения схемы, когда никаких действий еще не производилось? Еще нет логических операций и нет их результатов в виде каких-то логических состояний. Это состояние не вызывает никаких действий или других изменений. Что это?
Ни в Булевой, ни в троичной логике этому логическому состоянию нет отдельного названия. Если мы оцениваем его по состоянию информационных входов логических элементов, то это состояние совпадает с состоянием 0. Дальнейшие же действия предполагает только состояние 1. С любой полярностью.
С этих позиций можно условно разделить логические состояния системы на активные (1) и пассивное состояние ожидания действий — (0).
В Булевой логике одно активное состояние, а в троичной – два. Они, в конечном итоге и определяют возможности системы.
Но, это скорее теоретическое деление, в реальности все сложнее. От недостатка логических состояний системы и состоянию 0 нашли достаточное действенное применение. В электрических схемах все состояния относительны.
Как надо понимать все эти ДА, НЕТ, НЕ ЗНАЮ при решении задачи? Как написано, или в контексте задачи? Любой иностранец, наверное, чокнется при переводе такого простейшего диалога:
Мы же, не задумываясь, определим, что основное в ответе — НЕТ. Оказывается, что контекстное, локальное значение логического ответа почти всегда важнее его формального понимания. Так ли нам необходимо глобальное формальное различие логических состояний, как логических ответов системы, например, на уровне полярности источника питания?
Возможно, что вполне достаточным будет их различие только в пределах логической операции?
Что действительно требует глобального определения, так это состояние (0). Отсутствие всякого присутствия…, ждем-с. Начальное состояние ожидания или просто, ждущий режим. Все остальные, кстати, активные логические состояния (вот это и есть их глобальное определение), вполне могут иметь лишь локальные различия. ДА, НЕТ, НЕ ЗНАЮ, в конце концов…, так они называются в пределах логической операции. А вне ее –только единичные импульсы или потенциалы. Независимо от бывших различий.
Ситуация не такая уж заумная. И вполне разрешимая. Как математически, так и технически.
А пока, глобальные логические состояния можно разделить на два класса:
Пассивное состояние у нас пока одно, начальное. Когда никаких действий еще не производилось, или это состояние введено, как прерывание. В последнем случае оно может отображать только состояние входов логической схемы любого уровня, независимо от остальных ее внутренних состояний.
Активные логические состояния отражают все логические ответы той или иной логической системы. В этом случае Булева логика имеет одно такое состояние, а принятая троичная логика – два.
В связи с вышесказанным возникает некоторое противоречие. Состояние 0, это логическое состояние, которое не должно быть логическим ответом системы. Все логические ответы системы должны описываться только активными логическими состояниями. Только так можно надежно отделить начальное состояние или введенное прерывание работы логической системы от состояния неопределенного, но разрешенного системой логического ответа, полученного в результате решения задачи.
Таким образом, активные логические состояния определяют все логические ответы системы.
И как следствие из этого – логические ответы системы локальны. Они различны только в пределах Результата решения одной операции или задачи.
На любом другом уровне это лишь информационный импульс. Как наличие Результата после проведения логической операции.
Такое понимание логического состояния и логического ответа в корне отличается от принятого сегодня в математической и электронной логике. Сегодня нет различий между логическими состояниями и логическими ответами. И в Булевой, и в троичной логике это – одно и то же.
Разделение понятий глобальных логических состояний и локальных логических ответов дает возможность посмотреть на математическую логику с другой стороны.
Логический ответ и логическое состояние, это не одно и то же.
Логическое состояние не всегда может быть логическим ответом системы, но любой логический ответ является одним из логических состояний системы.
Начнем мы с логических ответов системы. Минимальный состав логических ответов нам знаком еще со времен греческой софистики, это — ДА и НЕТ.
Рассмотрим эти ответы с точки зрения логики, математики и условий бинарной записи.
Главное условие системы: Ни логические ответы, ни их противоположности не должны быть равными. Установим это условие через неравенства:
ДА 


А так выглядит взаимная противоположность логических ответов:
ДА = 
НЕТ =
Такая запись противоположности говорит, что логическая противоположность еще не означает их однозначной математической противоположности.
Отрицательности может и не быть. Это мы уже знаем.
С другой стороны, и каждый логический ответ имеет свою противоположность:
ДА = | 
НЕТ = | 
Это выражается в математическом равенстве величины ответа и абсолютной величины противоположности этого ответа.
Вводим условие неотрицательности ответов:
ДА 
НЕТ 
Равносильность логических ответов можно выразить через равенство их абсолютных величин:
|ДА | = |НЕТ|
| 

При: ДА 
Бинарная запись, являющаяся пока единственным математическим аналогом логического ответа оставляет нам только один вариант, подтверждающий математическую справедливость выражений:
| 

Математический эквивалент логических ответов оказывается одинаковым, но это противоречит условию их неравенства.
Это противоречие можно преодолеть введение понятия направления действия. Логические ответы имеют одинаковый вес по абсолютной величине, но различное направление действия, являясь при этом взаимно противоположными величинами и не имея однозначной математической отрицательности.
Вводим направление действия логического ответа:
ДА = 
НЕТ | =
Введением этого параметра мы сохраняем равный абсолютный вес величины математического эквивалента 1 вместе с сохранением взаимной противоположности действенных логических ответов системы.
Этим действием мы ввели пространственную координату в математику логики.
Логические ответы получили противоположную направленность при сохранении положительного математического весового эквивалента.
С одной стороны, это логическая неопределенность. А с другой – равенство аргументов ДА и НЕТ в Результате решения. Или их недостаточность для четкого выбора определенного действенного ответа.
В конце концов, количество НЕ ЗНАЮ в решении задачи определяет достоверность появления ДА или НЕТ в Результате. Если НЕ ЗНАЮ появилось многократно, то любой из ответов ДА или НЕТ в Результате уже не может быть признан абсолютно достоверным.
Мы введем этот логический ответ в нашу систему:
Его математический эквивалент, естественно будет:
И в то же время, неопределенный ответ (Х) не является определенным логическим ответам, т.к. не имеет направления действия:
ДА, НЕТ 




Прямую противоположность здесь ввести трудно. Но, на основании формул (25,26, 29, 30) можно установить, что:
| 


И логический ответ НЕ ЗНАЮ можно получить из ДА и НЕТ.
ДА 









С точки зрения математики это эквивалентно только одному выражению:
1 
Так как абсолютная величина всех логических ответов одинакова и равна 1.
С другой стороны, ответ НЕ ЗНАЮ — сумма аргументов, т.е. ДА и НЕТ, и для него должно быть справедливым выражение:
ДА + НЕТ = 





ДА + НЕТ = 





Утверждения (34) и (35) согласуются с ответом, получаемым в утверждении (32).
Операция дизъюнкции в Булевой логике имеет альтернативный характер по отношению к конъюнкции. В то же время эти операции очень взаимосвязаны.
Если в электронной схеме «И» изменить подключение к общему «0» с одного вывода питания на другой не меняя полярности питания, то мы получим «ИЛИ», и наоборот.
Для математики такой давно известный в электронике «электрический фокус» означает изменение умножения на сложение и обратно для одной и той же электронной схемы, в зависимости от изменения условий ее работы.
Это отражено и математике Булевой логики:
1+1 =1, 1 
1 
Формально, верный для Булевой логики вариант равенства. Вынужденное равенство.
Это же равенство можно использовать в интересном примере.