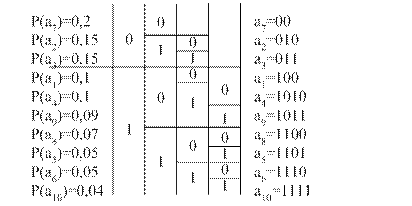коды шеннона фано и хаффмена
Сравнительная характеристика Шеннона-Фано и Хаффмана (кодов)
Primary tabs
Forums:
Методика Шеннона–Фано не всегда приводит к однозначному построению кода.
Ведь при разбиении на подгруппы на 1-й итерации можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. В результате среднее число символов на букву окажется другим.
Таким образом, построенный код может оказаться не самым лучшим.
От указанного недостатка свободна методика Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Метод Хаффмана производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Результаты эффективного кодирования по методу Хаффмана всегда лучше результатов кодирования по методу Шеннона-Фано.
Предложенный Хаффманом алгоритм построения оптимальных неравномерных кодов – одно из самых важных достижений теории информации, как с теоретической, так и с прикладной точек зрения. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия.
Трудно поверить, но этот алгоритм был придуман в 1952 г. студентом Дэвидом Хаффманом в процессе выполнения домашнего задания =).
Кодирование методом Хаффмана называют двухпроходным, так как его реализация распадается на два этапа:
Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана.
Код Шеннона-Фано
Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.
Рис. Кодовое дерево кода Шеннона – Фано
Методика Шеннона – Фано не всегда приводит к однозначному построению кода, поскольку при разбиении на части можно сделать больше по вероятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспечивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмеченных недостатков.
Код Хаффмана
Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.
Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последовательное ветвление продолжается до тех пор, пока не дойдем до вероятности каждой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.
Коды шеннона фано и хаффмена
Коды Фано и Хаффмана являются оптимальными и префиксными. При построении искомых кодов будем применять как традиционный табличный способ кодирования, так и использовать «кодовые деревья».
При кодировании по Фано все сообщения записываются в таблицу по степени убывания вероятности и разбиваются на две группы примерно (насколько это возможно) равной вероятности. Соответственно этой процедуре из корня кодового дерева исходят два ребра, которым в качестве весов присваиваются полученные вероятности. Двум образовавшимся вершинам приписывают кодовые символы 0 и 1. Затем каждая из групп вероятностей вновь делится на две подгруппы примерно равной вероятности. В соответствии с этим из каждой вершины 0 и 1 исходят по два ребра с весами, равными вероятностям подгрупп, а вновь образованным вершинам приписывают символы 00 и 01, 10 и 11. В результате многократного повторения процедуры разделения вероятностей и образования вершин приходим к ситуации, когда в качестве веса, приписанного ребру бинарного дерева, выступает вероятность одного из данных сообщений. В этом случае вновь образованная вершина оказывается листом дерева, т.к. процесс деления вероятностей для нее завершен. Задача кодирования считается решенной, когда на всех ветвях кодового бинарного дерева образуются листья.
Пример 151. Закодировать по Фано сообщения, имеющие следующие вероятности:
| сообщение | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| вероятность | 0,4 | 0,2 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 |
Решение 1 (с использованием кодового дерева)
Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами.
Решение 2 (табличный способ)
Цена кодирования (средняя длина кодового слова является критерием степени оптимальности кодирования. Вычислим ее в нашем случае.
Для того, чтобы закодировать сообщения по Хаффману, предварительно преобразуется таблица, задающая вероятности сообщений. Исходные данные записываются в столбец, две последние (наименьшие) вероятности в котором складываются, а полученная сумма становится новым элементом таблицы, занимающим соответствующее место в списке убывающих по величине вероятностей. Эта процедура продолжается до тех пор, пока в столбце не останутся всего два элемента.
Пример 152. Закодировать сообщения из предыдущего примера по методу Хаффмана.
Решение 1. Первый шаг
Вторым шагом производим кодирование, «проходя» по таблице справа налево (обычно это проделывается в одной таблице):
Решение 2. Построение кодового дерева начинается с корня. Двум исходящим из него ребрам приписывается в качестве весов вероятности 0,6 и 0,4, стоящие в последнем столбце. Образовавшимся при этом вершинам дерева приписываются кодовые символы 0 и 1. Далее «идем» по таблице справа налево. Поскольку вероятность 0,6 является результатом сложения двух вероятностей 0,4 и 0,2, из вершины 0 исходят два ребра с весами 0,4 и 0,2 соответственно, что приводит к образованию двух новых вершин с кодовыми символами 00 и 01. Процедура продолжается до тех пор, пока в таблице остаются вероятности, получившиеся в результате суммирования. Построение кодового дерева заканчивается образованием семи листьев, соответствующих данным сообщениям с присвоенными им кодами. Дерево, полученное в результате кодирования по Хаффману, имеет следующий вид:
Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами. Таблица кодов имеет вид:
| сообщение | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| код | 1 | 01 | 0010 | 0011 | 0000 | 00010 | 00011 |
Цена кодирования здесь будет равна
Для передачи данных сообщений можно перейти от побуквенного (поцифрового) кодирования к кодированию «блоков», состоящих из фиксированного числа последовательных «букв».
Пример 154. Провести кодирование по Хаффману трехбуквенных комбинаций для алфавита из предыдущего примера.
Построим кодовое дерево.
Найдем цену кодирования
Решение. Составим таблицу тройного «сжатия» по методу Хаффмана
Тогда тринарное дерево выглядит следующим образом:
Вопросы для самоконтроля
1. Как определяется среднее число элементарных сигналов, приходящихся на одну букву алфавита?
3. Сколько требуется двоичных знаков для записи кодированного сообщения?
4. На чем основано построение кода Фано?
5. Что такое сжатие алфавита?
6. Какой код самый выгодный?
7. Основная теорема о кодировании.
8. Энтропия конкретных типов сообщений.
I 301. Проведите кодирование по методу Фано алфавита из четырех букв, вероятности которых равны 0,4; 0,3; 0,2 и 0,1.
302. Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Фано.
304. Проведите кодирование по методу Хаффмана трехбуквенных слов из предыдущей задачи.
305. Проведите кодирование 7 букв из задачи 302 по методу Хаффмана.
306. Проведите кодирование по методам Фано и Хаффмана пяти букв, равновероятно встречающихся.
II 307. Осуществите кодирование двухбуквенных комбинаций четырех букв из задачи 301.
308. Проведите кодирование всевозможных четырехбуквенных слов из задачи 303.
III 309. Сравните эффективность кодов Фано и Хаффмана при кодировании алфавита из десяти букв, которые встречаются с вероятностями 0,3; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05; 0,04; 0,03; 0,03.
310. Сравните эффективность двоичного кода Фано и кода Хаффмана при кодировании алфавита из 16 букв, которые встречаются с вероятностями 0,25; 0,2; 0,1; 0,1; 0,05; 0,04; 0,04; 0,04; 0,03; 0,03; 0,03; 0,03; 0,02; 0,02; 0,01; 0,01.
Разница между кодированием Хаффмана и кодированием Шеннона Фано
Содержание
Здесь код префикса означает код, в котором никакое кодовое слово не образует префикс любого другого кодового слова.
Сравнительная таблица
| Основа для сравнения | Кодирование Хаффмана | Шеннон Фано Кодинг |
|---|---|---|
| Базовый | На основе вероятностей символа источника | На основе кумулятивной функции распределения |
| Эффективность | Лучше | Умеренный |
| Разработано | Дэвид Хаффман | Клод Шеннон и Роберт Фано |
| Изобретено в году | 1952 | 1949 |
| Предусмотрена оптимизация | Высоко | Низкий |
Определение кодирования Хаффмана
Он работает путем перевода символов, содержащихся в файле данных, в двоичный код. Однако основные символы в файле имеют наименьший двоичный код, а наименее встречающиеся символы имеют наибольший двоичный код. Это широко используемый метод сжатия текста без потерь, при котором сжатые данные могут быть восстановлены в исходном формате.
Теперь давайте разберемся с алгоритмом с помощью нескольких шагов:
Определение кодирования Шеннона Фано
Подобно кодированию Хаффмана, алгоритм Шеннона Фано используется для создания уникально декодируемого кода. Он был разработан Клодом Шенноном и Робертом Фано в 1949 году раньше, чем алгоритм кодирования Хаффмана. Этот метод также использует вероятности данных для их кодирования. Хотя это не обеспечивает оптимальную генерацию кода. Он рассматривается как метод построения префиксных кодов в соответствии с группой символов и вероятностей.
Кроме того, длина кодового слова кодов l (x) = [log 1 / P (x)], и они известны как коды Шеннона. Как упомянуто выше, длина кодового слова Шеннона удовлетворяет условию неравенства Крафт и может использоваться для генерации однозначно декодируемых кодов.
Здесь приведены шаги для интерпретации алгоритма:
Вывод
Среди обоих методов кодирования кодирование Хаффмана более эффективно и оптимально, чем кодирование Фано Шеннона.
СОДЕРЖАНИЕ
Именование
Что касается путаницы в двух разных кодах, называемых одним и тем же именем, Крайчи и др. Пишут:
Причин такой путаницы несколько. Во-первых, при обсуждении своей схемы кодирования Шеннон упоминает схему Фано и называет ее «практически такой же» (Шеннон, 1948, стр. 17). С другой стороны, схемы кодирования Шеннона и Фано схожи в том смысле, что они обе являются эффективными, но неоптимальные схемы кодирования без префиксов с аналогичной производительностью.
Код Шеннона: предопределенные длины слов
Алгоритм Шеннона
Метод Шеннона начинается с определения длины всех кодовых слов, а затем выбирается префиксный код с этими длинами слов.
Как только длины кодовых слов определены, мы должны выбрать сами кодовые слова. Один из методов состоит в том, чтобы выбрать кодовые слова в порядке от наиболее вероятных до наименее вероятных символов, выбирая каждое кодовое слово как лексикографически первое слово правильной длины, которое поддерживает свойство отсутствия префиксов.
Пример
В этом примере показано построение кода Шеннона – Фано для небольшого алфавита. Есть 5 разных исходных символов. Предположим, что наблюдались всего 39 символов со следующими частотами, по которым мы можем оценить вероятности символов.
| Символ | А | B | C | D | E |
|---|---|---|---|---|---|
| Считать | 15 | 7 | 6 | 6 | 5 |
| Вероятности | 0,385 | 0,179 | 0,154 | 0,154 | 0,128 |
Мы можем выбирать кодовые слова по порядку, выбирая лексикографически первое слово правильной длины, которое поддерживает свойство отсутствия префиксов. Очевидно, A получает кодовое слово 00. Для сохранения свойства отсутствия префиксов кодовое слово B может не начинаться с 00, поэтому лексикографически первым доступным словом длины 3 является 010. Продолжая таким образом, мы получаем следующий код:
В качестве альтернативы мы можем использовать метод совокупной вероятности.
Обратите внимание, что хотя кодовые слова в двух методах различаются, длины слов одинаковы. У нас есть длина 2 бита для A и 3 бита для B, C, D и E, что дает среднюю длину
2 биты ⋅ ( 15 ) + 3 биты ⋅ ( 7 + 6 + 6 + 5 ) 39 символы ≈ 2,62 бит на символ, <\ displaystyle <\ frac <2 \, <\ text
что находится в пределах одного бита энтропии.
Ожидаемая длина слова
Для метода Шеннона длины слов удовлетворяют
Следовательно, ожидаемая длина слова удовлетворяет
Код Фано: двоичное расщепление
Наброски кода Фано
В методе Фано символы располагаются в порядке от наиболее вероятного к наименее вероятному, а затем делятся на два набора, суммарные вероятности которых максимально близки к равенству. Затем всем символам присваиваются первые цифры их кодов; символы в первом наборе получают «0», а символы во втором наборе получают «1». Пока остаются любые наборы с более чем одним элементом, тот же процесс повторяется для этих наборов, чтобы определить последовательные цифры их кодов. Когда набор сокращен до одного символа, это означает, что код символа завершен и не будет образовывать префикс кода любого другого символа.
Алгоритм производит довольно эффективные кодировки переменной длины; когда два меньших набора, полученные в результате разделения, фактически равновероятны, один бит информации, используемый для их различения, используется наиболее эффективно. К сожалению, кодирование Шеннона – Фано не всегда дает оптимальные префиксные коды; набор вероятностей <0,35, 0,17, 0,17, 0,16, 0,15>является примером того, которому будут назначены неоптимальные коды с помощью кодирования Шеннона – Фано.
Дерево Шеннона – Фано
Дерево Шеннона – Фано строится в соответствии со спецификацией, разработанной для определения эффективной кодовой таблицы. Фактический алгоритм прост:
Пример
Продолжим предыдущий пример.
| Символ | А | B | C | D | E |
|---|---|---|---|---|---|
| Считать | 15 | 7 | 6 | 6 | 5 |
| Вероятности | 0,385 | 0,179 | 0,154 | 0,154 | 0,128 |
Все символы отсортированы по частоте слева направо (как показано на рисунке а). Проведение разделительной линии между символами B и C дает в общей сложности 22 в левой группе и всего 17 в правой группе. Это сводит к минимуму разницу в итогах между двумя группами.
При таком делении каждый из A и B будет иметь код, начинающийся с 0 бита, а коды C, D и E будут начинаться с 1, как показано на рисунке b. Впоследствии левая половина дерева получает новое деление между A и B, которое помещает A на лист с кодом 00 и B на лист с кодом 01.
После четырех процедур деления получается дерево кодов. В окончательном дереве трем символам с наивысшими частотами всем были присвоены 2-битные коды, а двум символам с меньшим счетом присвоены 3-битные коды, как показано в таблице ниже:
| Символ | А | B | C | D | E |
|---|---|---|---|---|---|
| Вероятности | 0,385 | 0,179 | 0,154 | 0,154 | 0,128 |
| Первая дивизия | 0 | 1 | |||
| Второй дивизион | 0 | 1 | 0 | 1 | |
| Третий дивизион | 0 | 1 | |||
| Кодовые слова | 00 | 01 | 10 | 110 | 111 |
Это приводит к длине 2 бита для A, B и C и на 3 бита для D и E, что дает среднюю длину
2 биты ⋅ ( 15 + 7 + 6 ) + 3 биты ⋅ ( 6 + 5 ) 39 символы ≈ 2,28 бит на символ. <\ displaystyle <\ frac <2 \, <\ text
Мы видим, что метод Фано со средней длиной 2,28 превосходит метод Шеннона со средней длиной 2,62.
Ожидаемая длина слова
Сравнение с другими методами кодирования
Кодирование Хаффмана
Несколькими годами позже Дэвид А. Хаффман (1949) дал другой алгоритм, который всегда дает оптимальное дерево для любой заданной вероятности символа. В то время как дерево Шеннона – Фано Фано создается путем деления от корня до листьев, алгоритм Хаффмана работает в противоположном направлении, сливаясь от листьев к корню.
Пример с кодировкой Хаффмана
Мы используем те же частоты, что и в приведенном выше примере Шеннона – Фано, а именно:
| Символ | А | B | C | D | E |
|---|---|---|---|---|---|
| Считать | 15 | 7 | 6 | 6 | 5 |
| Вероятности | 0,385 | 0,179 | 0,154 | 0,154 | 0,128 |
В этом случае D и E имеют самые низкие частоты, поэтому им присваиваются 0 и 1 соответственно, и они сгруппированы вместе с общей вероятностью 0,282. Самой младшей парой теперь являются B и C, поэтому им присваиваются 0 и 1 и они сгруппированы вместе с общей вероятностью 0,333. Это оставляет BC и DE с наименьшими вероятностями, поэтому к их кодам добавляются 0 и 1, и они объединяются. После этого остаются только A и BCDE, к которым добавлены 0 и 1 соответственно, и затем они объединяются. Это оставляет нам единственный узел, и наш алгоритм завершен.
Длина кода для разных символов на этот раз составляет 1 бит для A и 3 бита для всех остальных символов.
| Символ | А | B | C | D | E |
|---|---|---|---|---|---|
| Кодовые слова | 0 | 100 | 101 | 110 | 111 |
Это приводит к длине 1 бита для A и 3 бита для B, C, D и E, что дает среднюю длину
1 немного ⋅ 15 + 3 биты ⋅ ( 7 + 6 + 6 + 5 ) 39 символы ≈ 2,23 бит на символ. <\ displaystyle <\ frac <1 \, <\ text
Мы видим, что код Хаффмана превзошел оба типа кода Шеннона – Фано, которые имели ожидаемые длины 2,62 и 2,28.