кто придумал двоичный код для компьютера
Двоичный код — где и как применяется?
Сегодня я по-особому рад своей встрече с вами, дорогие мои читатели, ведь я чувствую себя учителем, который на самом первом уроке начинает знакомить класс с буквами и цифрами. А поскольку мы живем в мире цифровых технологий, то я расскажу вам, что такое двоичный код, являющийся их основой.
Начнем с терминологии и выясним, что означит двоичный. Для пояснения вернемся к привычному нам исчислению, которое называется «десятичным». То есть, мы используем 10 знаков-цифр, которые дают возможность удобно оперировать различными числами и вести соответствующую запись.
Следуя этой логике, двоичная система предусматривает использование только двух знаков. В нашем случае, это всего лишь «0» (ноль) и «1» единица. И здесь я хочу вас предупредить, что гипотетически на их месте могли бы быть и другие условные обозначения, но именно такие значения, обозначающие отсутствие (0, пусто) и наличие сигнала (1 или «палочка»), помогут нам в дальнейшем уяснить структуру двоичного кода.
Зачем нужен двоичный код?
До появления ЭВМ использовались различные автоматические системы, принцип работы которых основан на получении сигнала. Срабатывает датчик, цепь замыкается и включается определенное устройство. Нет тока в сигнальной цепи – нет и срабатывания. Именно электронные устройства позволили добиться прогресса в обработке информации, представленной наличием или отсутствием напряжения в цепи.
Дальнейшее их усложнение привело к появлению первых процессоров, которые так же выполняли свою работу, обрабатывая уже сигнал, состоящий из импульсов, чередующихся определенным образом. Мы сейчас не будем вникать в программные подробности, но для нас важно следующее: электронные устройства оказались способными различать заданную последовательность поступающих сигналов. Конечно, можно и так описать условную комбинацию: «есть сигнал»; «нет сигнала»; «есть сигнал»; «есть сигнал». Даже можно упростить запись: «есть»; «нет»; «есть»; «есть».
Но намного проще обозначить наличие сигнала единицей «1», а его отсутствие – нулем «0». Тогда мы вместо всего этого сможем использовать простой и лаконичный двоичный код: 1011.
Безусловно, процессорная техника шагнула далеко вперед и сейчас чипы способны воспринимать не просто последовательность сигналов, а целые программы, записанные определенными командами, состоящими из отдельных символов.
Но для их записи используется все тот же двоичный код, состоящий из нулей и единиц, соответствующий наличию или отсутствию сигнала. Есть он, или его нет – без разницы. Для чипа любой из этих вариантов – это единичная частичка информации, которая получила название «бит» (bit — официальная единица измерения).
Условно, символ можно закодировать последовательностью из нескольких знаков. Двумя сигналами (или их отсутствием) можно описать всего четыре варианта: 00; 01;10; 11. Такой способ кодирования называется двухбитным. Но он может быть и:
Скажу честно, единой официальной версии нет, то так сложилось, что именно комбинация из восьми знаков стала стандартной мерой хранящейся информации, именуемой «байт». Таковая могла применяться даже к одной букве, записанной 8-и битным двоичным кодом. Итак, дорогие мои друзья, запомните пожалуйста (если кто не знал):
Так принято. Хотя символ, записанный 2-х или 32-х битным значением так же номинально можно назвать байтом. Кстати, благодаря двоичному коду мы можем оценивать объемы файлов, измеряемые в байтах и скорость передачи информации и интернета (бит в секунду).
Бинарная кодировка в действии
Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:
Расшифровка значений в ней показано в таблице.
Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:
Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.
Язык, понятный современной технике
Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:
Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:
Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.
Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.
Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.
Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.
Двоичный код использовали сотни лет назад
Считается, что двоичная арифметика, основа цифровых вычислений, была изобретена в начале XVIII века немецким математиком Готфридом Лейбницем. Однако исследование, проведенное учеными из Университета Бергена в Норвегии, показывает, что своеобразная система двоичного счисления уже использовалась 300 лет назад народом, проживающим на крошечном тихоокеанском острове Мангареву во Французской Полинезии. До сих пор этот удивительный факт оставался неизвестным, поскольку после колонизации аборигены Мангареву начали приобщаться к европейской культуре, и к настоящему времени система коренных жителей острова уже давно заменена арабскими цифрами и современными методиками счета. Кроме того, на острове проживают всего 600 местных жителей, которые сохранили лишь крупицы древних знаний. Тем не менее, норвежским ученым удалось реконструировать некоторые понятия языка аборигенов Мангареву, в том числе используя труды исследователей XIX – начала XX века.
Колонизация уничтожила оригинальную систему счета аборигенов Мангареву, однако ученые смогли восстановить сложную двоичную/десятичную систему счисления
Открытие норвежских ученых позволяет предположить, что некоторые из преимуществ двоичной системы Лейбница уже использовались аборигенами Мангареву. Древние люди смогли создать эту методику интуитивно, даже в обществе без передовой науки и техники, опираясь лишь на стремление обеспечить удобство счета в торговле.
Сотни лет назад количество жителей Мангареву составляло несколько тысяч. Это было высоко стратифицированное общество, которое выживало благодаря добыче морепродуктов и выращиванию корнеплодов. Для совершения сложных крупных сделок аборигенам Мангареву потребовалась соответствующая система счета.
В то же самое время, смешанная десятичная/двоичная система Мангареву действительно необычна. Удивительно, что на крошечном острове с небольшим населением была создана столь сложная система счета. Сам этот факт также показывает, насколько важны методики счета для развития культуры. В случае с Мангареву необходимость работы с большими числами мотивировала людей на поиски нестандартных решений.
История двоичного кода
Автор работы: Пользователь скрыл имя, 26 Июня 2013 в 10:54, реферат
Краткое описание
Идея использования лишь двух символов для кодирования информации стара, как мир. Барабаны, которыми пользуются некоторые племена африканских бушменов, передают сообщения в виде комбинаций звонких и глухих ударов. Другой, более современный пример двухсимвольного кодирования – азбука Морзе, в которой буквы алфавита представлены определенными сочетаниями точек и тире. Австралийские аборигены считали двойками, некоторые племена охотников-сборщиков Новой Гвинеи и Южной Америки тоже пользовались двоичной системой счета.
Содержание
1. Введение.
2. История зарождения двоичного кода.
3. Основоположники двоичного кода.
4. Заключение.
5. Список источников.
6. Глоссарий.
Вложенные файлы: 1 файл
фи-31.История двоичного кода (реферат).doc
То, что связь между человеком, высадившимся на Луне, и Землей, праздновавшей это событие, осуществлялась при помощи нулей и единиц, глубоко символично и закономерно, потому что эти знаки двоичной системы счисления сыграли в этом историческом достижении тысячи всевозможных ролей. С их помощью было закодировано все – от команд, отданных космическому кораблю при взлете, до инструкций, благодаря которым спускаемый аппарат экспедиции Армстронга при возвращении на Землю вошел в земную атмосферу под соответствующим углом. То же самое происходит повсюду в нашем компьютеризованном мире. В основе своей цифровой компьютер независимо от его размеров и назначения представляет систему передачи информации, выраженной в виде нулей и единиц.
Идея использования лишь двух символов для кодирования информации стара, как мир. Барабаны, которыми пользуются некоторые племена африканских бушменов, передают сообщения в виде комбинаций звонких и глухих ударов. Другой, более современный пример двухсимвольного кодирования – азбука Морзе, в которой буквы алфавита представлены определенными сочетаниями точек и тире. Австралийские аборигены считали двойками, некоторые племена охотников-сборщиков Новой Гвинеи и Южной Америки тоже пользовались двоичной системой счета.
Двоичное представление чисел – не единственная альтернатива десятичной системе счисления. Древняя вавилонская арифметика была основана на числе 60, а в привычках и языке англосаксов мы обнаруживаем следы двенадцатеричной системы счисления, которая когда-то господствовала на Британских островах: 12 месяцев в году, 12 дюймов в футе, два 12-часовых периода в сутках, различные системы мер, также основанные на числе 12. Вызванная к жизни не чем иным, как десятью пальцами пары человеческих рук, десятичная система в конце концов вытеснила все другие системы счета, по крайней мере в странах Запада. Однако некоторые европейские мыслители эпохи Просвещения, последовавшей за эпохой Возрождения, проявляли немалый интерес к простой и изящной двоичной системы счисления. Постепенно эта система проникала из одной научной дисциплины в другую, из логики и философии в математику, а затем и в технику, где она сыграла важную роль на заре компьютерной революции.
История зарождения двоичного кода.
Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен.
Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики.
Индийский математик Пингала ра зработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.
Узелковые носители информации «кипу», которыми инки пользовались вместо письменности, являются аналогом современного двоичного кода. К такому выводу пришел гарвардский исследователь древней южноамериканской цивилизации Гари Эртон.
По утверждению Эртона узелки на шнурках, завязанные инками, представляют собой 7-битный двоичный код и могут передавать до 1500 отдельных знаков.
Продолжая поиски твердого доказательства своей теории, профессор Эртон надеется в ближайшее время найти южноамериканский «камень Розетты» – повествование на «кипу», более 400 лет назад переведенную на испанский язык. Говоря о камне Розетты, ученый из США имеет в виду базальтовую плиту, найденную в Розетте, недалеко от египетского города Александрия. Эта находка содержала билингву и позволила египтологам расшифровать значение египетских иероглифов.
Согласно результатам исследований Эртона, у инков существовало семь способов завязывания «кипу». Общее число вариантов, полученных при сочетании различных методов вязания, достигает 128. Однако, как отмечает ученый, с учетом использования инками шнурков 24 цветов число комбинаций «кипу» достигает 1536.
Выводы Эртона говорят о том, что, применяя «кипу», инки по количеству возможных к передаче знаков превзошли шумеров с их приблизительно 1000-1500 информационными блоками и в два раза превысили количество иероглифов египтян и майя. Если выводы профессора найдут подтверждение, получится, что инки изобрели двоичный код, как минимум, за 500 лет до появления компьютера и использовали его в трехмерной письменности.
Впрочем, без латиноамериканского «камня Розетты» доказать теорию Эртона будет очень непросто.
Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
Основоположники двоичной системы.
Современники Лейбница, возможно, слегка озадаченные, а может быть, и возмущенные его предложением, оставили работу ученого без внимания, да и сам Лейбниц, по-видимому, не стал развивать идею нового языка. Однако десятилетие спустя он занялся исследованием строгих математических законов применительно к новой области – двоичной системе счисления. На кропотливой работе по переводу чисел из десятичной системы в двоичную его вдохновляла старинная рукопись, случайно попавшаяся ему на глаза. Это был комментарий по поводу знаменитой китайской книги «Ай чинг» (Книга перемен), в которой делалась попытка описать Вселенную во всей ее сложности с помощью ряда философских категорий противоположностей – например, таких понятий, как темнота и свет, мужское и женское начало. Ободренный этим созвучием со своими математическими концепциями Лейбниц терпеливо исследовал бесконечные комбинации нулей и единиц, формализуя найденные им закономерности и закладывая тем самым основы современной двоичной системы.
Однако при всей своей гениальности Лейбниц так и не смог найти полезного применения полученным результатам.
Однако спустя более ста лет после смерти Лейбница (1716) английский математик-самоучка Джордж Буль энергично принялся за поиски такого универсального языка. Примечательно, что этой целью задался человек такого скромного происхождения, как Буль. Он был родом из бедной рабочей семьи, жившей в промышленном городе Линкольне в восточной Англии. В те времена мальчик, родители которого были простыми рабочими, вряд ли мог надеяться получить солидное образование, а тем более сделать карьеру ученого. Однако решимость и целеустремленность Буля не знали границ.
В Линкольне была школа для мальчиков. Возможно, Буль посещал ее, но если и так, то там он мог получить лишь самое элементарное образование. Однако его отец, самостоятельно овладевший кое-какими познаниями в математике, передал эти знания своему способному сыну. Уже к восьми годам мальчика всецело захватила жажда знаний. Предметом, который, по-видимому, сыграл важную роль в дальнейшей судьбе Буля, был латинский язык. Здесь отец ничем не мог ему помочь, но друг их семьи, занимавшийся книжной торговлей, в достаточной степени владел латинской грамматикой, чтобы дать Булю начальный толчок. Когда книготорговец обучил его всему, что знал сам, Буль продолжил учебу самостоятельно и в возрасте 12 лет уже переводил классическую латинскую поэзию. Еще через два года он овладел греческим языком, а затем добавил к своей коллекции языков французский, немецкий и итальянский.
В 1831 г. в возрасте 16 лет Буль был вынужден поступить на работу, чтобы помочь семье. Четыре года он проработал на малооплачиваемой должности помошника учителя, но затем, осмелев, решил открыть собственную школу. Поняв, что ему следует углубить свои познания в математике, чтобы превзойти учеников, он приступил к чтению математических журналов, которые имелись в библиотеке местного научного учреждения. И тут у Буля обнаружились поистине неординарные способности. Изучив горы научных публикаций, он овладел сложнейшими математическими теориями своего времени. У него возникли и собственные оригинальные идеи. Буль стал записывать их, не прекращая в то же время преподавательской работы в своей маленькой школе. В 1839 г. одна из его статей была принята к публикации научным журналом. На протяжении следующего десятилетия работы Буля регулярно печатались, и его имя приобрело известность в научных кругах. В конце концов деятельность Буля получила столь высокую оценку, что он, несмотря на отсутствие формального образования, был приглашен работать на математический факультет Королевского колледжа в Ирландии.
Большинство логиков того времени либо игнорировали, либо резко критиковали систему Буля, но ее возможности оказались настолько велики, что она не могла долго оставаться без внимания.
Американский логик Чарлз Сандерс Пирс познакомил в 1867 г. с булевой алгеброй американскую научную общественность, кратко изложив существо этой системы в своем докладе для Американской академии наук и искусств. На протяжении двух последующих десятилетий Пирс затратил немало времени и сил, модифицируя и расширяя булеву алгебру. Он осознал, что бинарная логика Буля хорошо подходит для описания электрических переключательных схем. Например, ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным. Электрический переключатель действует во многом сходно с логическим вентилем, либо пропуская ток (что соответствует значению «истина»), либо нет. Самого Пирса гораздо больше интересовала логика, чем электричество. И хотя позже он придумал простую электрическую логическую схему, она не была собрана.
Тем не менее, внедрив булеву алгебру в курсы логики и философии в американских университетах, Пирс посеял семена, которые дали богатые всходы пол столетия спустя. В 1936 г. выпускник американского университета Клод Шеннон, которому было тогда всего 21 год, сумел ликвидировать разрыв между алгебраической теорией и ее практическим приложением.
В то время Шеннон только что перешел в Массачусетский технологический институт (МТИ) из Мичиганского университета, где получил два диплома бакалавра – по электротехнике и по математике. Желая подработать, Шеннон выполнял обязанности оператора на неуклюжем механическом вычислительном устройстве под названием «дифференциальный анализатор», который построил в 1930 г. научный руководитель Шеннона профессор В. Буш. Это была первая машина, способная решать сложные дифференциальные уравнения, которые позволяли предсказывать поведение таких движущихся объектов, как самолет, или действие силовых полей, например гравитационного поля. На решение подобных уравнений вручную уходили иногда целые месяцы, так что дифференциальный анализатор имел важное научное значение. Однако он обладал многими серьезными недостатками. Прежде всего это его гигантские размеры: подобно старинной Аналитической машине Бэббиджа, механический анализатор Буша представлял собой сложную систему валиков, шестеренок и проволок, соединенных в серию больших блоков, которые занимали целую комнату. Столь большие габариты устройства отчасти объяснялись тем, что расчеты проводились в десятичной системе счисления. Однако размеры это не единственный недостаток анализатора. Он был аналоговым устройством, которое само измеряло скорость и анновере, а затем на основе измеренных величин проводило расчеты. Чтобы поставить машине задачу, оператор вынужден был вручную подбирать множество шестереночных передач, на что уходило 2 – 3 дня. При любом изменении параметров задачи оператору приходилось изрядно потрудиться и перепачкаться в машинном масле.
Как объяснять двоичную систему счисления
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить. Слишком быстро проскочили идею о переносе разряда.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):
Значение двоичного кода – почему компьютеры работают с единицами и нулями
Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
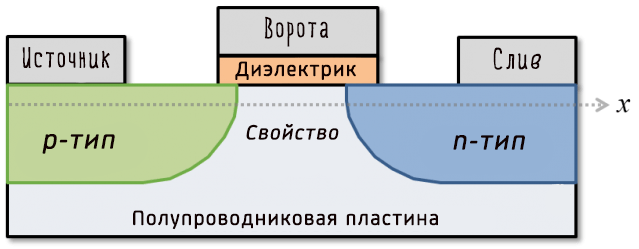
Вот схема типичного транзистора:
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
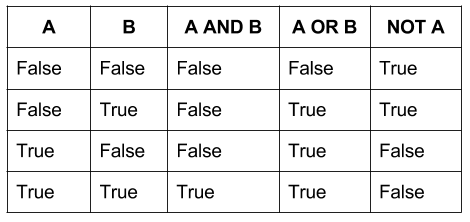
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.
Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.