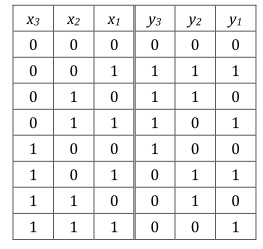
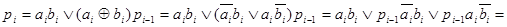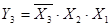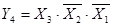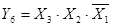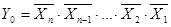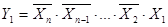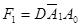логический алгоритм синтеза устройства для формирования n разрядного дополнительного кода имеет вид
Синтез преобразователя внутренних кодов на примере дополнительного кода
Различают алгоритмы арифметических и логических типов формирования дополнительных кодов. Алгоритмы первого типа требуют для реализации последовательностных цифровых схем, т.е. схем с элементами памяти. При этом для получения дополнительного n- разрядного двоичного кода до 2 n необходимо выполнить инверсию этого кода и суммировать с единицей младшего разряда.
Подобные алгоритмы реализуют на параллельных регистрах в универсальных обработчиках информации. Альтернативой подобных алгоритмов для КЛС может служить алгоритм, синтезируемый с использованием следующей таблицы истинности (табл.4.9):
| 10 эквив. | Двоичный код | Дополнительный код | 10 эквив. | ||||
| В4 | В3 | В2 | В1 | D4 | D3 | D2 | D1 |
Синтез преобразователя двоичных кодов в дополнительный на базе КЛС выполним начиная с младшего разряда, для этого составим матицу Карно для функции D1=F(B4, B3, B2,B1).
| В4, В3 |
| 00 01 11 10 |
| В2,B1 |
| В4, В3 |
| 00 01 11 10 |
| В2,B1 |
 |
| В4, В3 |
| 00 01 11 10 |
| B2,B1 |
Логический алгоритм синтеза устройства для формирования n–разрядного дополнительного кода может быть представлен для любого разряда выражением вида :
Дополнив его выражениями для D1, D2, получим замкнутый алгоритм для получения дополнительного кода.
Синтез комбинационных устройств на примере преобразователя из прямого кода в дополнительный
Вся окружающая нас электроника состоит из отдельных микросхем, более сложная электроника – из построенных на их основе функциональных блоков.
На данном этапе компьютеры буквально создают сами себя, стало невозможно синтезировать даже самый простой микропроцессор без применения вычислительного устройства.
Но что же все-таки лежит в основе самой микросхемы? Как создать простейшее цифровое устройство с требуемой выходной функцией?
Под катом — пример синтеза устройства со всей необходимой теорией.
Немного теории
Все элементарные цифровые устройства (ЦУ) делятся на комбинационные и последовательностные. В комбинационных ЦУ выходные сигналы однозначно определяются комбинацией входных сигналов, действующих в данный момент. Выходные сигналы (функции) последовательностных ЦУ определяются последовательностью изменения входных сигналов (координат).
В основе практически всех цифровых микросхем лежат простейшие логические элементы И, ИЛИ, НЕ. Естественно, что вариантов реализации ЦУ может быть очень много, в зависимости от комбинаций составных элементарных логических элементов. Поэтому оговоримся заранее, что синтез будем производить в базисе И-НЕ, т.е. используем в ходе построения ЦУ только этот элемент.
Думаю, что аудитория Хабра знает основы алгебры логики. Приведу только парочку формул:
Постановка задачи
В данной статье рассмотрим пример синтеза последовательностного ЦУ. В качестве примера возьмем преобразователь из прямого кода в дополнительный (для трехразрядного кода).
Дополнительный код числа образуется путем прибавления 1 к младшему разряду инвертированного числа. Например, имеем число А = 10110 (старший разряд слева). Тогда обратный код для А — 01001, а дополнительный — 01010.
Синтез устройства
Для начала составим таблицу истинности.
Обозначения: х — входные сигналы, у — выходные. Индекс «1» — у младшего бита.
Теперь необходимо выразить выходные сигналы в зависимости от входных с помощью простейших логических функций (по условию задания, будем пользоваться базисом И-НЕ).
Чаще всего используют две формы записи — совершенную дизъюнктивную нормальной форму (СДНФ) и совершенную конъюнктивную нормальную форму (СКНФ).
В первом случае, каждому набору переменных из таблицы истинности ставится в соответствие минтерм — логическое произведение всех переменных, которые входят в прямом виде, если значение переменной равно 1, или в инверсном виде, если значение переменной равно 0. Любую логическую функцию можно представить в виде логической суммы минтермов, соответствующих единичным наборам переменных (наборам, при которых логическая функция принимает значение 1). Такое представление и называется СДНФ. Для реализации ЦУ в базисе И-НЕ целесообразно представлять выходную функцию именно в виде СДНФ.
В случае СКНФ все прямо противоположно. Функция представляется в виде логического произведения макстермов. Макстерм — логическая сумма всех переменных, которые входят в прямом виде, если значение переменной равно 0, или в инверсном виде, если значение переменной равно 1.
Запишем выходную функцию y1 в виде СДНФ:
Карты Карно
Видно, что выражение получилось достаточно длинным. Его можно упростить, применяя правила поглощения и склеивания. Для того, чтобы не делать лишних действий, можно сразу получить минимизированную функцию. Для этого можно применить метод карт Карно.
Карта представляет собой таблицу, каждая клетка которой соответствует одному из наборов таблицы истинности. Для логической функции трех переменных карта Карно представляет собой два горизонтальных ряда по четыре клетки. Смысл применения карт Карно определяется специально выбранным порядком нумерации клеток, при котором любой соседней паре клеток с единицами или нулями по горизонтали или вертикали соответствуют склеивающиеся слагаемые или сомножители формулы. Если структурная формула получается на основе СДНФ, то учитываются только клетки карты, определяющие единичные наборы. (В случае СКНФ — нулевые).
Соседние клетки карты с единицами или нулями объединяются в группу. При объединении пользуются следующими правилами:
1) соседними являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки на противоположных краницах карты;
2) клетки могут объединяться по 2, по 4, по 8 и т.д.;
3) одна и та же клетка может входить в несколько групп;
4) минимизированная структурная формула записывается на основе наименьшей совокупности групп, которая захватывает (покрывает) все либо единичные (если используется СДНФ), либо нулевые (СКНФ) клетки.
В первом случае структурная формула предстваляет собой логическую сумму, каждое из слагаемых которой соответствует одной из групп карты. При этом в каждое слагаемое входят лишь те переменные, которые не меняют своего значения в наборах, соответствующих объединенным клеткам. Во втором случае в группы объединяют нулевые клетки, минимизированная структурная формула представляет собой логическое произведение, каждый сомножитель которого записывается на основе группы карты.
Далее будем указывать в наших картах только единичные наборы. «Нулевые» клетки будем оставлять пустыми.
Пора уже начинать.
Итак, приступим к синтезу нашего устройства, руководствуясь вышеизложенной теорией.
Для начала составим карты Карно для всех выходных функций (их у нас три, как и входных). Кружочком помечены клетки, объединяемые в одну группу. Обратите внимание, суммируем произведения неизменяющихся (в данной группе )входных сигналов с соответствующим логическим уровнем. Количесвто слагаемых равно количеству групп-объединений. В первой карте объединены 2-я и 3-я клетки, а также 3-я и 4-я. Во второй — 2-я и 6-я, а также 4-я и 8-я. В третьей карте в одну группу объединены 2, 3, 6, 7-я клетки.
Далее справа записываем в соответствии с правилами объединения клеток минимизированные выходные функции. Т.к. нам нужно получить их в определенном базисе, применяем алгебру логики, а именно формулы (1) и (2) и выражаем функции через входные переменные.
Теперь можем синтезировать наше ЦУ по полученным функциям:
Получили готовое цифровое устройство —преобразователь трехразрядного кода из прямого в дополнительный.
Не знаю, насколько актуален вышеизложенный метод синтеза. Постарался все изложить на том уровне, на каком понимаю данную тему сам. Жду комментов от компетентных хабровчан.
Литература:
Цифровые и аналого-цифровые устройства / А. В. Логинов, Ан. В. Логинов. ЛМИ, 1989
Тема 4. Комбинационные цифровые устройства



4-1. Понятие комбинационного цифрового устройства, микросхемы комбинационного типа малой степени интеграции.
Под комбинационным цифровым устройством (КЦУ) понимается цифровое устройство, обеспечивающее преобразование совокупности N входных цифровых сигналов в M выходных, при этом состояние выходных сигналов в данный момент времени определяется состоянием входных сигналов в этот же момент времени. Иными словами, КЦУ «не помнит» предыстории поступления сигналов на его входы. Правила функционирования КЦУ определяются реализуемыми ими функциями алгебры логики.
Реализация КЦУ предполагает выбор определенных логических элементов из заданного набора и их соединение таким образом, чтобы обеспечивалась зависимость цифровых выходных сигналов от входных с заданными правилами функционирования. При реализации КЦУ широко используются интегральные комбинационные логические микросхемы малой степени интеграции, образующие основу элементной базы цифровой электроники. В настоящее время, как в нашей стране, так и за рубежом, выпускается широкая номенклатура комбинационных микросхем малой степени интеграции ТТЛ-, ЭСЛ- и КМОП-типов. При выборе конкретной микросхемы необходимо руководствоваться видом реализуемой ею логической функции, быстродействием, нагрузочной способностью и возможностью совместимости электрических характеристик входных и выходных сигналов с остальными элементами схемы.
Отдельно следует отметить класс микросхем, способных принимать третье пассивное Z-состояние или, как его еще называют, высокоимпедансное состояние. Такое состояние характеризуется высоким внутренним сопротивлением входов или выходов, благодаря которому они оказываются как бы отключенными от информационных цепей схемы. Признаком наличия Z-состояния является символ «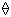
Как было отмечено раньше, при выборе цифровых микросхем необходимо учитывать возможность согласования энергетических уровней их входных и выходных сигналов. Одним из способов согласования уровней ТТЛ и КМОП является выбор микросхем ТТЛ-типа с открытыми коллекторами и подтягивание уровней логических единиц их выходов до логических единиц уровня КМОП с помощью подтягивающих резисторов. Существуют специально разработанные для этих целей микросхемы согласования уровней. Функция согласования логических уровней задается символами ПУ в маркировке микросхемы.
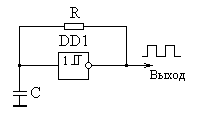
При формировании сигналов ТТЛ- или КМОП-уровней из аналогового сигнала, например из синусоиды, при обработке сигналов в условиях большого уровня помех, а также в генераторах импульсов широкое применение нашли цифровые триггеры Шмитта. Характерной особенность этих элементов является наличие гистерезиса на их передаточной характеристике (рис. 4.1). При плавном изменении входного сигнала у триггера Шмитта происходит скачкообразное изменение выходного, причем пороги срабатывания при переходе из нуля в единицу и из единицы в нуль отличаются.
Рис. 4.1. Передаточная характеристика триггера Шмитта ТТЛ-типа.
Рис. 4.2. Схема автоколебательного мультивибратора на базе цифрового триггера Шмитта.
В случаях, когда часть входов многовходовых элементов остается незадействованной, на неиспользуемые входы этих элементов необходимо подавать логические нули или логические единицы в зависимости от логики выполняемой операции. Так если неиспользуемыми являются отдельные входы элемента И, то, чтобы результат операции не исказился, на них необходимо подавать напряжения логической единицы. Сделать это можно, подключив неиспользуемые входы элемента И через ограничительный резистор к источнику питания. Если неиспользуемыми являются входы элемента ИЛИ, то их необходимо подключить через ограничительный резистор к нулевому потенциалу общего провода, подав на них, таким образом, уровень напряжения логического нуля. Неиспользуемые входы можно объединять с используемыми. Результаты операций И и ИЛИ в этом случае не изменятся, но входные токи объединенных выводов возрастут. Если же количества входов элемента наоборот недостаточно, то возможно наращивание входов схемы путем пирамидального объединения нескольких элементов. Пример подобных структур, позволяющих на базе двух четырехвходовых элементов осуществлять обработку восьми логических переменных, представлен на рис. 4.3. Первая структура реализует функцию логического умножения восьми переменных, а вторая – логического сложения.
Рис. 4.3. Наращивание входов для схем, реализующих функции И, ИЛИ.
В зарубежной литературе и многих компьютерных программах систем автоматизированного проектирования часто встречаются обозначения логических элементов, не соответствующие российским стандартам. На рис. 4.4 приведено соответствие функциональных обозначений некоторых базовых логических элементов согласно отечественным и зарубежным стандартам.
Рис. 4.4. Функциональные обозначения базовых логических элементов в отечественных и зарубежных стандартах.
4-2. Синтез комбинационного цифрового устройства.
Синтез КЦУ предусматривает построение структурной схемы устройства, т.е. определение состава необходимых логических элементов и соединений между ними, при которых обеспечивается преобразование входных цифровых сигналов в выходные в соответствии с заданными условиями работы устройства. В процессе синтеза обычно подразумевается необходимость минимизации аппаратных затрат на реализацию устройства. Рассмотрим синтез КЦУ с одним выходом. Последовательность синтеза целесообразно разбить на ряд этапов:
— запись условий функционирования КЦУ в виде таблиц истинности, логической функции, последовательности десятичных чисел или кубического комплекса;
— запись и минимизация СДНФ или СКНФ;
— запись минимизированной структурной формулы и ее преобразование с помощью законов и тождеств алгебры логики в заданном базисе, обычно И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ;
— оставление структурной схемы КЦУ, т.е. изображение нужных логических элементов и связей между ними.
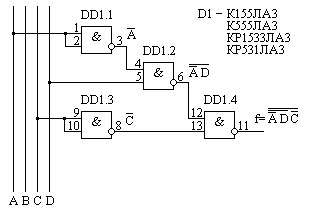
Проиллюстрируем пример синтеза КЦУ на элементах И-НЕ для реализации логической функции, заданной в виде десятичных цифр
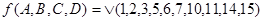
Структурная формула в СДНФ имеет вид
После выполнения процесса минимизации методами, рассмотренными в теме 1, получим МДНФ

Для перехода к заданному базису И-НЕ поставим два знака инверсии над правой частью формулы и применим к ней правило де Моргана. В результате получим структурную формулу в следующем виде:
Структурная схема синтезированного на основе заданных условий КЦУ и соответствующего полученной формуле приведена на рис. 4.5. Элемент DD1.1 инвертирует сигнал с линии А, элемент DD1.3 – с линии C. Поскольку 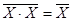
Рис. 4.5. Пример синтеза произвольного КЦУ.
На практике широко применяются КЦУ, имеющие несколько выходов. При проектировании таких устройств можно воспользоваться рассмотренным ранее аппаратом синтеза, если представить устройство в виде совокупности соответствующего числа КЦУ с общими входами. При построении сложных цифровых устройств широко применяются не только отдельные логические элементы, реализующие элементарные булевы функции, но и их комбинации в виде типовых структур, выполненных как единое целое в виде интегральных микросхем. На входы таких структур могут подаваться информационные логические сигналы и сигналы управления. Последние могут определять порядок передачи информационных входных сигналов на выход, задавать состояние трехуровневых выходов элементов или играть роль сигналов синхронизации. Перейдем к рассмотрению типовых комбинационных устройств и начнем с сумматоров.
4-3. Сумматоры.
| Входы | Выходы | ||
| А | В | Sп/см. | Pп/см. |
Записанные по таблице истинности ФАЛ для переменных Sп/см. и Pп/см. имеют вид
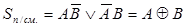

Рис. 4.6. Структурная схема и УГО полусумматора.
Полный одноразрядный сумматор выполняет операцию арифметического сложения двух одноразрядных чисел A и B с учетом переноса из младшего разряда Р-1. Он имеет три входа и два выхода. Работа полного одноразрядного сумматора задается таблицей истинности:
| Входы | Выходы | |||
| A | B | Р-1 | S | P |
Записав СДНФ для переменных S и P и выполнив ряд тождественных преобразований можно получить следующие ФАЛ для полного сумматора:

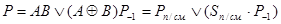
Выражение 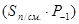
Рис. 4.7. Схема и УГО полного одноразрядного сумматора.
Из таблицы истинности полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – нуль при наличии единицы на одном из входах A, B или Р-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет нуль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 4.8.
Рис. 4.8. Структурная схема одноразрядного полного сумматора, положенная в основу микросхем ТТЛ-типа.
При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их необходимо соединить в последовательные структуры. Выходы переноса Р микросхем младших разрядов подключаются к входам переноса Р-1 микросхем старших разрядов. Отдельные разряды слагаемых подаются на входы А и В микросхем соответствующих разрядов, а с их выходов S снимаются разряды результата суммирования. Выход переноса P микросхемы самого старшего разряда является выходом переноса результата суммирования всего n-разрядного числа.
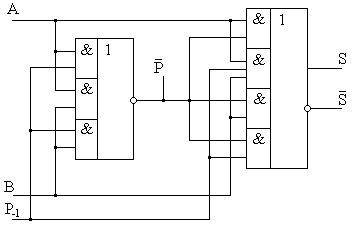
Такой способ наращивания разрядности сумматоров путем последовательного объединения нескольких полных сумматоров меньшей разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Распространение переноса в таких структурах осуществляется последовательно от микросхемы к микросхеме. Этого недостатка лишены сумматоры с параллельным переносом. Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду
Введем обозначения 
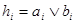

В общем случае можно записать

где 



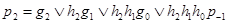
Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для pi каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы pi с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 4.9.
Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом реализуют обычно для сложения чисел с разрядностью не более четырех бит.
При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации.
Рис. 4.9. Схема четырехразрядного сумматора с параллельным переносом.
Второй подход также основан на использовании набора сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат.
4-4. Дешифраторы и шифраторы.
| Входы | Выходы | |||||||||
| X3 | X2 | X1 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
Соответствующие таблице истинности ФАЛ имеют вид

Рис. 4.10. Структурная схема и УГО трехразрядного дешифратора.
В общем случае логические уравнения для выходных переменных дешифратора n-разрядного числа имеют вид
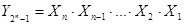
Построенные по полученным формулам дешифраторы называются линейными. К преимуществу линейных дешифраторов можно отнести высокое быстродействие, поскольку входные переменные одновременно поступают на все элементы И. Одновременно, без дополнительных задержек, формируется и результат на выходах этих элементов. Очевидно, что для реализации линейного дешифратора n-разрядного числа необходимо иметь 2 n логических элементов И с n-входами. В существующих микросхемах логических элементов количество входов ограничено. Следовательно, ограничена и разрядность реализуемых на их основе линейных дешифраторов, что является недостатком. Кроме того, недостатком является и то, что предыдущие элементы, работающие на входы дешифратора, должны иметь высокую нагрузочную способность, т.е. должны быть рассчитаны на подключение большого числа логических элементов И. Каждый из входов дешифратора подключен к 0,5·2 n логическим элементам И. Поскольку нагрузочная способность базовых логических элементов ИС не превышает величины N=10¸20, то максимальная разрядность дешифрируемых чисел для линейных дешифраторов n=4¸5.
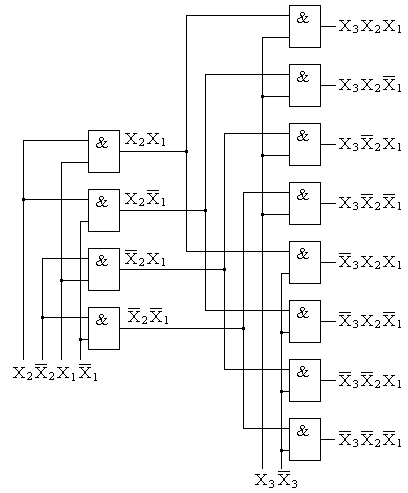
Указанного недостатка лишены пирамидальные дешифраторы. Принцип построения этих дешифраторов состоит в том, что сначала строят линейный дешифратор для двухразрядного числа X1, X2, для чего необходимы 2 2 =4 двухвходовые схемы И. Далее, каждая полученная конъюнкция логически умножается на входную переменную X3 в прямой и инверсной форме. Полученная конъюнкция снова умножается на входную переменную X4 в прямой и инверсной форме и т.д. Наращивая таким образом структуру, можно построить пирамидальный дешифратор на произвольное число входов. На рис. 4.11 приведена структура пирамидального дешифратора для трех разрядов.
Рис. 4.11. Пирамидальный дешифратор для трехразрядного числа.
Характерным отличием пирамидальных дешифраторов от линейных является использование только двухвходовых логических элементов вне зависимости от разрядности дешифрируемого числа. В то же время количество логических элементов в пирамидальном дешифраторе больше. Однако следует иметь ввиду, что количество логических элементов, располагаемых в одном корпусе ИС, определяется главным образом требуемым количеством выводов. Следовательно, в одном корпусе ИС можно расположить большее число двухвходовых элементов, чем трехвходовых, четырехвходовых и т.д. И значит, пирамидальная структура дешифратора по числу корпусов ИС может оказаться более предпочтительной, чем линейная.
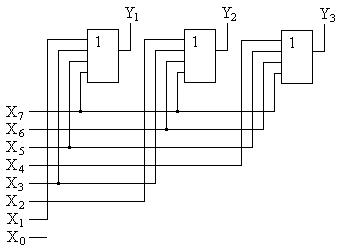
Шифраторы выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе приводит к появлению соответствующей кодовой комбинации на выходе. Также как и дешифраторы, шифраторы бывают полными и неполными. Работа восьмивходового полного шифратора задается следующей таблицей истинности:
| Входы | Выходы | |||||||||
| X7 | X6 | X5 | X4 | X3 | X2 | X1 | X0 | Y3 | Y2 | Y1 |
На основании таблицы истинности можно записать ФАЛ, задающие работу восьмивходового шифратора:
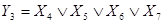
Синтезированная на основании приведенных логических уравнений структурная схема шифратора представлена на рис. 4.12,а, а его условное графическое обозначение – на рис. 4.12,б.
Рис. 4.12. Структура и УГО восьмивходового шифратора.
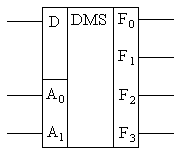
4-5. Мультиплексоры и демультиплексоры.
| Входы | Выход | |
| A1 | A0 | F |
| D0 | ||
| D1 | ||
| D2 | ||
| D3 |
Логическое выражение для выходной функции, заданной таблицей, можно записать в виде
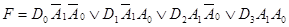
В соответствии с полученной формулой для реализации мультиплексора можно использовать логические элементы И, ИЛИ, НЕ. Синтезированная структурная схема мультиплексора показана на рис. 4.13,а, а его условное графическое обозначение – на рис. 4.13,б.
Рис. 4.13. Структура и УГО мультиплексора «из 4 в 1».
Мультиплексирование при большом числе входов можно выполнить пирамидальным каскадированием мультиплексоров, как это показано на рис. 4.14. На рисунке показано каскадирование мультиплексоров «из 4 в 1» для реализации функции мультиплексирования «из 16 в 1».
Рис. 4.14. Пирамидальное каскадирование мультиплексоров.
Мультиплексоры первого уровня управляются адресными сигналами А0 и А1, а мультиплексоры второго – адресными сигналами А2 и А3. Каждый из мультиплексоров первого уровня выбирает один из четырех разрядов Dj. Первый мультиплексор выбирает один из разрядов D0 – D3, второй мультиплексор – один из разрядов D4 – D7 и т.д. Выходы с мультиплексоров первого уровня объединяются в мультиплексоре второго уровня, который осуществляет окончательную коммутацию и формирование выходного сигнала F.
Мультиплексор можно реализовать, используя дешифратор и схемы И и ИЛИ (рис. 4.15). Дешифратор формирует логическую единицу на одном из выходов согласно входному двоичному коду. Сигналы с выходов дешифратора являются стробирующими, т.е. разрешающими сигналами для схемы совпадения единиц, реализованной на двухвходовых элементах И. Логическая единица будет формироваться на выходе только того элемента И, на один вход которого подается единица с выхода дешифратора и на второй вход – единица с соответствующего входа Dj. Для объединения выходов всех элементов И в один выход F, служит элемент ИЛИ. На его выходе формируется логическая единица, если таковая присутствует на опрашиваемом в данный момент входе Dj.
Рис. 4.15. Реализация мультиплексора на базе дешифратора.
Демультиплексор выполняет функцию, обратную мультиплексору, т.е. в соответствии с принятой адресацией Ai направляет информацию с единственного входа D на один из M выходов Fj. При этом на остальных выходах будут логические нули (единицы). Принцип работы демультиплексора «из 1 в 4» иллюстрируется таблицей истинности:
| Входы | Выходы | ||||
| A1 | A0 | F3 | F2 | F1 | F0 |
| D | |||||
| D | |||||
| D | |||||
| D |
Логические выражения для каждого из выходов можно представить в виде:
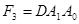
Структурная схема, реализующая демультиплексор «из 1 в 4» приведена на рис. 4.16,а, а его условное графическое обозначение – на рис. 4.16,б.
Как и в случае мультиплексора, схему демультиплексора можно реализовать с помощью дешифратора. Действительно, ФАЛ демультиплексора отличается от ФАЛ дешифратора только наличием входного сигнала D в конъюнкциях с адресными входами. Следовательно, объединив выходы дешифратора с входом D с помощью стробирующих элементов И, можно получить демультиплексор (рис. 4.17). Мультиплексоры и демультиплексоры часто называют еще цифровыми коммутаторами.
Рис. 4.16. Структурная схема и УГО демультиплексора «из 1 в 4».
Рис. 4.17. Реализация демультирлексора на базе дешифратора.
4-6. Цифровые компараторы.
| Входы | Выход | |
| ai | bi | yi |
Определим ФАЛ для yi, соответствующую приведенной таблице истинности

Синтезированная структурная схема в соответствии с формулой для yi имеет вид, изображенный на рис. 4.18.
Рис. 4.18. Структурная схема устройства сравнения одноразрядных кодов.
Проинвертируем функцию yi и преобразуем ее, используя законы отрицания алгебры логики: 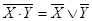


т.е. окончательно имеем инверсию функции Исключающее ИЛИ.
Для перехода от равенства отдельных разрядов к функции равенства Y всего кода необходимо установить факт наличия логических единиц во всех n разрядах. Это осуществляется схемой И на n входов (рис. 4.19). ФАЛ для функции Y имеет вид

Рис. 4.19. Структурная схема компаратора двух четырехразрядных чисел.
Выпускаемые промышленностью цифровые компараторы устанавливают обычно не просто факт равенства или неравенства чисел А и В, но и определяют большее из них, т.е. устанавливают следующие соотношения чисел А и В: A>B, A