лох в двоичном коде
двоичный код в текст
Преобразуйте двоичный текст в текстовый / английский или ASCII, используя prepostseoБинарный переводчик. Введите двоичные числа (например, 01000101 01111000 01100001 01101101 01110000 01101100 01100101) и нажмите кнопку Преобразовать
Двоичный переводчик
Двоичная система счисления
Система двоичного декодера основана на числе 2 (основание). Он состоит только из двух чисел как системы счисления base-2: 0 и 1.
Хотя бинарная система применялась в различных целях в древнем Египте, Китае и Индии, она стала языком электроники и компьютеров современного мира. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала. Это также основа двоичного кода в текст, который используется на компьютерах для составления данных. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел. Но вы можете прочитать этот текст, потому что мы расшифровали двоичный код перевод файл, используя двоичный код слова.
Двоичное число легче прочитать, чем выглядит: это позиционная система; поэтому каждая цифра двоичного числа возводится в степень 2, начиная с 20 справа. Каждая двоичная цифра в преобразователе двоичного кода относится к 1 биту.
Что такое ASCII?
Бинарный в ASCII
Первоначально основанный на английском алфавите, ASCII кодирует 128 указанных семибитных целочисленных символов. Можно печатать 95 кодированных символов, включая цифры от 0 до 9, строчные буквы от a до z, прописные буквы от A до Z и символы пунктуации. Кроме того, 33 непечатных контрольных кода, полученных с помощью машин Teletype, были включены в исходную спецификацию ASCII; большинство из них в настоящее время устарели, хотя некоторые все еще широко используются, такие как возврат каретки, перевод строки и коды табуляции.
Использование ASCII
Как уже упоминалось выше, используя ASCII, вы можете перевести компьютерный текст в человеческий текст. Проще говоря, это переводчик с бинарного на английский. Все компьютеры получают сообщения в двоичном, 0 и 1 серии. Тем не менее, так же, как английский и испанский могут использовать один и тот же алфавит, но для многих похожих слов у них совершенно разные слова, у компьютеров также есть своя языковая версия. ASCII используется как метод, который позволяет всем компьютерам обмениваться документами и файлами на одном языке.
ASCII важен, потому что при разработке компьютерам был дан общий язык.
До декабря 2007 года, когда кодировка UTF-8 превосходила ее, ASCII была наиболее распространенной кодировкой символов во Всемирной паутине; UTF-8 обратно совместим с ASCII.
UTF-8 (Юникод)
Unicode и универсальный набор символов (UCS) ISO / IEC 10646 имеют гораздо более широкий диапазон символов, и их различные формы кодирования начали быстро заменять ISO / IEC 8859 и ASCII во многих ситуациях. Хотя ASCII ограничен 128 символами, Unicode и UCS поддерживают большее количество символов посредством разделения уникальных концепций идентификации (с использованием натуральных чисел, называемых кодовыми точками) и кодирования (до двоичных форматов UTF-8, UTF-16 и UTF-32-битных). ).
Разница между ASCII и UTF-8
ASCII был включен как первые 128 символов в набор символов Unicode (1991), поэтому 7-разрядные символы ASCII в обоих наборах имеют одинаковые числовые коды. Это позволяет UTF-8 быть совместимым с 7-битным ASCII, поскольку файл UTF-8 с только символами ASCII идентичен файлу ASCII с той же последовательностью символов. Что еще более важно, прямая совместимость обеспечивается, поскольку программное обеспечение, которое распознает только 7-битные символы ASCII как специальные и не изменяет байты с самым высоким установленным битом (как это часто делается для поддержки 8-битных расширений ASCII, таких как ISO-8859-1), будет сохранить неизмененные данные UTF-8.
Приложения переводчика двоичного кода
• Наиболее распространенное применение для этой системы счисления можно увидеть в компьютерных технологиях. В конце концов, основой всего компьютерного языка и программирования является двузначная система счисления, используемая в цифровом кодировании.
• Это то, что составляет процесс цифрового кодирования, беря данные и затем изображая их с ограниченными битами информации. Ограниченная информация состоит из нулей и единиц двоичной системы. Изображения на экране вашего компьютера являются примером этого. Для кодирования этих изображений для каждого пикселя используется двоичная строка.
• Если на экране используется 16-битный код, каждому пикселю будут даны инструкции, какой цвет отображать на основе того, какие биты равны 0 и 1. В результате получается более 65 000 цветов, представленных 2 ^ 16. В дополнение к этому вы найдете применение двоичной системы счисления в математической ветви, известной как булева алгебра.
• Ценности логики и истины относятся к этой области математики. В этом приложении заявлениям присваивается 0 или 1 в зависимости от того, являются ли они истинными или ложными. Вы можете попробовать преобразование двоичного в текстовое, десятичное в двоичное, двоичное в десятичное преобразование, если вы ищете инструмент, который помогает в этом приложении.
Преимущество двоичной системы счисления
Система двоичных чисел полезна для ряда вещей. Например, компьютер щелкает переключателями для добавления чисел. Вы можете стимулировать добавление компьютера, добавляя двоичные числа в систему. В настоящее время есть две основные причины использования этой компьютерной системы счисления. Во-первых, это может обеспечить надежность диапазона безопасности. Вторично и самое главное, это помогает минимизировать необходимые схемы. Это уменьшает необходимое пространство, потребляемую энергию и расходы.
Интересный факт
Вы можете кодировать или переводить двоичные сообщения, написанные двоичными числами. Например,
(01101001) (01101100011011110111011001100101) (011110010110111101110101) является декодированным сообщением. Когда вы скопируете и вставите эти цифры в наш бинарный переводчик, вы получите следующий текст на английском языке:
(01101001) (01101100011011110111011001100101) (011110010110111101110101) = Я тебя люблю
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Дубликаты не найдены
Большое спасибо! Очень хорошо объяснили. Всё понял.
Берем калькулятор и перемножая двойку саму на себя подбираем максимально близкое (но меньшее 85) число
Повторяем операцию для 21
Ближайшее 16, или 2 в 4 степени
Ближайшее 4, или 2^2
1, или 2 в степени 0.
Теперь собираем наше число, проставляя единицу для той степени двойки, которая у нас встретилась (т.е. 2^6 2^4 2^2 2^0) и нуль для той степени, которая не встрети лась (2^5 2^3 2^1)
2^6 2^5 2^4 2^3 2^2 2^1 2^0
спасибо, оч доступно)
Вот этот абзац объясняет принцип записи:
——
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
——
Можете в качестве обратной связи рассказать, что именно здесь не ясно? 🙂
«не хватает перевода из десятичной в двоичную»
Да, я уже осознал этот изъян и подготовил пост про перевод из десятичной в двоичную. Завтра выложу. 🙂
«и остальных операций двоичной арифметики»
Мне показалось, что для чайников это сложновато уже. Мне лично как программисту крайне редко приходится делать с двоичным кодом что-то из арифметики, кроме сложения.
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]= 100 «
и еще «= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Да просто.
6 = 1х2^2 +1х 2^1 + 0х2^0 = 110
7 = 1х2^2 + 1×2^1 + 1×2^0 = 111
7 = 4 +3 +1 = 100 + 010 + 001
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Ну, мы числа называем в десятичной системе, поэтому в простых случаях двоичное число переводят в десятичную в уме и так читают. 🙂
Ну ты же не называешь число В в HEX «одиннадцать», хотя оно именно 11?
Ну, и «B» я прочитаю как «одиннадцать» или как «бэ» в зависимости от контекста 🙂
Ну да. Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?
«Но у тебя в этой системе уже есть 11, и в десятичной это 17. Не путаешься?»
Не очень понял вопрос. Что с чем я должен путать, по-твоему?
«Ну а в двоичной системе, по которой ты строишь счет, понятия «два» не существует.»
Я утверждаю, что у многих чисел есть названия. И так сложилось исторически, что эти названия даны в десятичной системе.
Например, если я в унарной системе запишу:
111 + 1111 = 1111111
Я буду читать «три плюс четыре равно семь», а не «сто одиннадцать плюс тысяча сто одиннадцать равно один миллион сто тысяч. «.
Ты называл число В как 11, не смотря на то, что у тебя есть в этой же системе 11, эквивалентное десятичной 17.
Сбивает с толку? Да не больше, чем её графическая запись.
если с двоичной системы такие названия к проблемам восприятия могут и не привести, то в шестнадцатеричной точно будет путаница.
Держи мое объяснение:
Когда ты считаешь до десяти, у тебя в какой-то момент кончаются названия чисел и тебе приходится комбинировать названия, чтобы считать больше 9. Например:
Ну а в двоичной системе цифры кончаются уже после 1, так и живем:
Как ты понимаешь, от того, как мы назвали количество, само количество от этого не изменилось, изменился только способ счета.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
Неправильные примеры. Да и как такового знака + и * в булевой алгебре нет
На самом деле все еще проще.
нет есть способ проще, всмысле рассказать
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
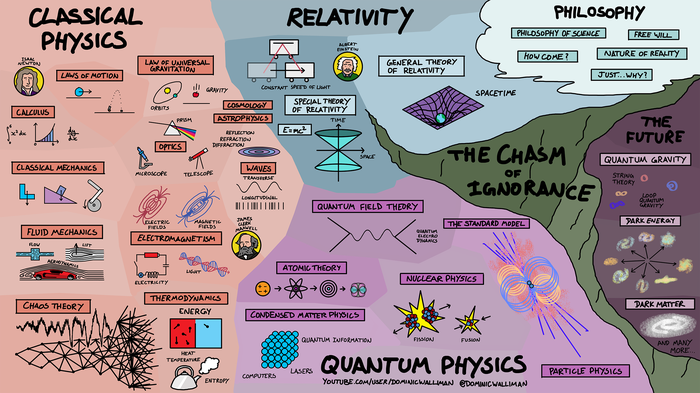
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.
Двоичный код.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.
На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.
Перевод натурального числа десятичной системы счисления в двоичную систему.
Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:
1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.
2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.
3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.
4. В этот момент считается, что двоичный код готов.
Для примера переведем в двоичную систему число 7:
1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.
2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.
3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.
4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.
Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.
Перевод числа двоичной системы в десятичную.
Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.
Немного из истории двоичной системы счисления.
Кодировка текста в двоичного код
Перевод текста в двоичный код
Существуют ASCII и двоичные представления для множества символов; пробелы, знаки препинания и буквы. А пока мы сосредоточимся на том, как переводить двоичный текст, используя только буквы. Первое, что нам нужно, это слово. Давайте использовать «собака», потому что кто не любит собак?
Мы видим, что символы dog соответствуют десятичным дробям 100, 111 и 103. Единственное, что осталось сделать, чтобы преобразовать наш текст в двоичный код, – это преобразовать десятичные числа в двоичный. Начиная со 100, нам нужно переопределить число, используя степень двойки.
Поскольку 100 не является степенью 2, найдите степень 2, которая равна или меньше 100. Мы можем переопределить 100 как 64 + 36. Поскольку 36 не является степенью 2, нам нужно переопределить это тоже. К счастью для нас, 36 можно переопределить как 32 + 4; больше степеней 2.
Почему ноль? Мы не можем использовать единицу без изменения всего значения двоичного кода. А в двоичном формате текстовые символы всегда начинаются с 010 или 011. 010 обозначает заглавную букву, а 011 обозначает строчную. Мы знаем, что наши буквы строчные, и если мы добавим этот ноль, у нас будет префикс 011. Теперь, когда мы добавили ноль, давайте посмотрим, что такое наш двоичный код. В двоичном формате «собака» выглядит так: 01100100 01101111 01100111.
Если вы хотите вставить в текст пробел, для этого тоже есть двоичный код. Простое нажатие клавиши пробела между символами на самом деле не означает пробел. Если мы хотим добавить второе слово к нашей фразе, нам понадобится двоичная строка « 00100000 » для разделения слов.
Представьте, что мы хотим сказать «хорошая собака». Во-первых, нам нужно найти десятичное значение первого слова. В кодировке ASCII «хорошо» представлены числами 103, 111, 111 и 100. Это те же десятичные дроби в первом слове, dog, так что вы уже знаете их двоичный вывод. Просто переставьте их, и вы сможете записать «хорошо» в двоичном формате.
Теперь давайте сложим их все вместе и не забываем строку, которая нам нужна для пробела между двумя словами. Вы можете использовать переводчик текста в двоичный код на этой странице, чтобы увидеть, как он должен выглядеть. Как вы, наверное, догадались, для короткой фразы это много двоичного кода. Переводчик с английского на двоичный полезен, если вам нужно преобразовать большой текст.
Как вы используете двоичный конвертер?
Наш конвертер очень проста в использовании.
Для этого достаточно одного простого шага: ввести (или вставить) текст в первое поле.
Слова будут преобразованы на лету, и двоичный код для вашего текста сразу появится в поле ниже.
Как преобразовать текст в двоичный?
Чтобы преобразовать английские слова (или любой текст ASCII) в двоичный, у вас есть два варианта: вы можете либо использовать онлайн-конвертер (например, тот, который предоставляется бесплатно на sas.com.ru), либо вы можете сделать это вручную.
Как работает двоичный конвертер?
Это очень просто: для каждого символа входящего текста (например, букв, цифр, знаков препинания) он ссылается на таблицу ASCII, чтобы определить числовой код ASCII для этого символа.
Могу ли я преобразовать двоичный формат в текст?
Конечно (при условии, что ваш двоичный код представляет символы ASCII)!
Если вам нужно преобразовать любой двоичный текст в ASCII, вы можете использовать двоичный переводчик текста.
Как мне написать свое имя в двоичном коде?
Вам просто нужно преобразовать каждую букву вашего имени в двоичную форму.
Попробуйте конвертер текста в двоичный, чтобы мгновенно преобразовать собственное имя в двоичный код!
Что такое «привет» в двоичном коде?
Слово «привет» в двоичном коде выглядит следующим образом: 0110100001100101011011000110110001101111. Разделив его на восьмизначные сегменты, легче увидеть двоичный байт, соответствующий каждой букве: 01101000 01100101 01101100 01101100 01101111
Таблица двоичного преобразования
| Символ ASCII | Шестнадцатеричные | Двоичные |
|---|---|---|
| NUL | 00 | 00000000 |
| SOH | 01 | 00000001 |
| STX | 02 | 00000010 |
| ETX | 03 | 00000011 |
| EOT | 04 | 00000100 |
| ENQ | 05 | 00000101 |
| ACK | 06 | 00000110 |
| BEL | 07 | 00000111 |
| BS | 08 | 00001000 |
| HT | 09 | 00001001 |
| LF | 0A | 00001010 |
| VT | 0B | 00001011 |
| FF | 0C | 00001100 |
| CR | 0D | 00001101 |
| SO | 0E | 00001110 |
| SI | 0F | 00001111 |
| DLE | 10 | 00010000 |
| DC1 | 11 | 00010001 |
| DC2 | 12 | 00010010 |
| DC3 | 13 | 00010011 |
| DC4 | 14 | 00010100 |
| NAK | 15 | 00010101 |
| SYN | 16 | 00010110 |
| ETB | 17 | 00010111 |
| CAN | 18 | 00011000 |
| EM | 19 | 00011001 |
| SUB | 1A | 00011010 |
| ESC | 1B | 00011011 |
| FS | 1C | 00011100 |
| GS | 1D | 00011101 |
| RS | 1E | 00011110 |
| US | 1F | 00011111 |
| Space | 20 | 00100000 |
| ! | 21 | 00100001 |
| “ | 22 | 00100010 |
| # | 23 | 00100011 |
| $ | 24 | 00100100 |
| % | 25 | 00100101 |
| & | 26 | 00100110 |
| ‘ | 27 | 00100111 |
| ( | 28 | 00101000 |
| ) | 29 | 00101001 |
| * | 2A | 00101010 |
| + | 2B | 00101011 |
| , | 2C | 00101100 |
| – | 2D | 00101101 |
| . | 2E | 00101110 |
| / | 2F | 00101111 |
| 0 | 30 | 00110000 |
| 1 | 31 | 00110001 |
| 2 | 32 | 00110010 |
| 3 | 33 | 00110011 |
| 4 | 34 | 00110100 |
| 5 | 35 | 00110101 |
| 6 | 36 | 00110110 |
| 7 | 37 | 00110111 |
| 8 | 38 | 00111000 |
| 9 | 39 | 00111001 |
| : | 3A | 00111010 |
| ; | 3B | 00111011 |
| 3E | 00111110 | |
| ? | 3F | 00111111 |
| @ | 40 | 01000000 |
| A | 41 | 01000001 |
| B | 42 | 01000010 |
| C | 43 | 01000011 |
| D | 44 | 01000100 |
| E | 45 | 01000101 |
| F | 46 | 01000110 |
| G | 47 | 01000111 |
| H | 48 | 01001000 |
| I | 49 | 01001001 |
| J | 4A | 01001010 |
| K | 4B | 01001011 |
| L | 4C | 01001100 |
| M | 4D | 01001101 |
| N | 4E | 01001110 |
| O | 4F | 01001111 |
| P | 50 | 01010000 |
| Q | 51 | 01010001 |
| R | 52 | 01010010 |
| S | 53 | 01010011 |
| T | 54 | 01010100 |
| U | 55 | 01010101 |
| V | 56 | 01010110 |
| W | 57 | 01010111 |
| X | 58 | 01011000 |
| Y | 59 | 01011001 |
| Z | 5A | 01011010 |
| [ | 5B | 01011011 |
| \ | 5C | 01011100 |
| ] | 5D | 01011101 |
| ^ | 5E | 01011110 |
| _ | 5F | 01011111 |
| ` | 60 | 01100000 |
| a | 61 | 01100001 |
| b | 62 | 01100010 |
| c | 63 | 01100011 |
| d | 64 | 01100100 |
| e | 65 | 01100101 |
| f | 66 | 01100110 |
| g | 67 | 01100111 |
| h | 68 | 01101000 |
| i | 69 | 01101001 |
| j | 6A | 01101010 |
| k | 6B | 01101011 |
| l | 6C | 01101100 |
| m | 6D | 01101101 |
| n | 6E | 01101110 |
| o | 6F | 01101111 |
| p | 70 | 01110000 |
| q | 71 | 01110001 |
| r | 72 | 01110010 |
| s | 73 | 01110011 |
| t | 74 | 01110100 |
| u | 75 | 01110101 |
| v | 76 | 01110110 |
| w | 77 | 01110111 |
| x | 78 | 01111000 |
| y | 79 | 01111001 |
| z | 7A | 01111010 |
| < | 7B | 01111011 |
| | | 7C | 01111100 |
| > | 7D | 01111101 |
| 7E | 01111110 | |
| DEL | 7F | 01111111 |
Accessibility
Accessibility modes
Online Dictionary
Readable Experience
Visually Pleasing Experience
Easy Orientation
SEO инструменты для оптимизации и продвижения сайта Accessibility Statement
Accessibility Statement
Compliance status
We firmly believe that the internet should be available and accessible to anyone, and are committed to providing a website that is accessible to the widest possible audience, regardless of circumstance and ability.
To fulfill this, we aim to adhere as strictly as possible to the World Wide Web Consortium’s (W3C) Web Content Accessibility Guidelines 2.1 (WCAG 2.1) at the AA level. These guidelines explain how to make web content accessible to people with a wide array of disabilities. Complying with those guidelines helps us ensure that the website is accessible to all people: blind people, people with motor impairments, visual impairment, cognitive disabilities, and more.
This website utilizes various technologies that are meant to make it as accessible as possible at all times. We utilize an accessibility interface that allows persons with specific disabilities to adjust the website’s UI (user interface) and design it to their personal needs.
Additionally, the website utilizes an AI-based application that runs in the background and optimizes its accessibility level constantly. This application remediates the website’s HTML, adapts Its functionality and behavior for screen-readers used by the blind users, and for keyboard functions used by individuals with motor impairments.
If you’ve found a malfunction or have ideas for improvement, we’ll be happy to hear from you. You can reach out to the website’s operators by using the following email
Screen-reader and keyboard navigation
Our website implements the ARIA attributes (Accessible Rich Internet Applications) technique, alongside various different behavioral changes, to ensure blind users visiting with screen-readers are able to read, comprehend, and enjoy the website’s functions. As soon as a user with a screen-reader enters your site, they immediately receive a prompt to enter the Screen-Reader Profile so they can browse and operate your site effectively. Here’s how our website covers some of the most important screen-reader requirements, alongside console screenshots of code examples:
Screen-reader optimization: we run a background process that learns the website’s components from top to bottom, to ensure ongoing compliance even when updating the website. In this process, we provide screen-readers with meaningful data using the ARIA set of attributes. For example, we provide accurate form labels; descriptions for actionable icons (social media icons, search icons, cart icons, etc.); validation guidance for form inputs; element roles such as buttons, menus, modal dialogues (popups), and others. Additionally, the background process scans all of the website’s images and provides an accurate and meaningful image-object-recognition-based description as an ALT (alternate text) tag for images that are not described. It will also extract texts that are embedded within the image, using an OCR (optical character recognition) technology. To turn on screen-reader adjustments at any time, users need only to press the Alt+1 keyboard combination. Screen-reader users also get automatic announcements to turn the Screen-reader mode on as soon as they enter the website.
These adjustments are compatible with all popular screen readers, including JAWS and NVDA.
Keyboard navigation optimization: The background process also adjusts the website’s HTML, and adds various behaviors using JavaScript code to make the website operable by the keyboard. This includes the ability to navigate the website using the Tab and Shift+Tab keys, operate dropdowns with the arrow keys, close them with Esc, trigger buttons and links using the Enter key, navigate between radio and checkbox elements using the arrow keys, and fill them in with the Spacebar or Enter key.Additionally, keyboard users will find quick-navigation and content-skip menus, available at any time by clicking Alt+1, or as the first elements of the site while navigating with the keyboard. The background process also handles triggered popups by moving the keyboard focus towards them as soon as they appear, and not allow the focus drift outside of it.
Users can also use shortcuts such as “M” (menus), “H” (headings), “F” (forms), “B” (buttons), and “G” (graphics) to jump to specific elements.
Disability profiles supported in our website
Additional UI, design, and readability adjustments
Browser and assistive technology compatibility
We aim to support the widest array of browsers and assistive technologies as possible, so our users can choose the best fitting tools for them, with as few limitations as possible. Therefore, we have worked very hard to be able to support all major systems that comprise over 95% of the user market share including Google Chrome, Mozilla Firefox, Apple Safari, Opera and Microsoft Edge, JAWS and NVDA (screen readers), both for Windows and for MAC users.
Notes, comments, and feedback
Despite our very best efforts to allow anybody to adjust the website to their needs, there may still be pages or sections that are not fully accessible, are in the process of becoming accessible, or are lacking an adequate technological solution to make them accessible. Still, we are continually improving our accessibility, adding, updating and improving its options and features, and developing and adopting new technologies. All this is meant to reach the optimal level of accessibility, following technological advancements. For any assistance, please reach out to