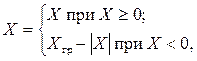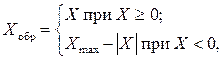машинные формы представления чисел с фиксированной запятой прямой обратный и дополнительный коды

Прямые, обратные и дополнительные коды чисел с фиксированной запятой

ЭВМ выполняет арифметические операции над числами с фиксированной запятой в машинных кодах. Простейшим машинным кодом является прямой код.

Прямой код числа Х аналогичен двоичному коду, но число его разрядов строго определено и положение двоичной точки в самом коде никак не указано.

Прямые коды чисел просты, но плохо приспособлены для выполнения операций алгебраического сложения и вычитания чисел. Проще и быстрее выполняются операции алгебраического суммирования, вычитания и деления в дополнительных или обратных кодах.

Дополнительный код двоичного числа Х, представленного в n-разрядной сетке, определяется как

Таким образом, дополнительный код положительного числа совпадает с прямым кодом, а дополнительный код отрицательного числа получается как дополнение до граничного числа.

Обратный код двоичного числа Х, представленного в n-разрядной сетке, определяется как

Граничное значение Х_гротличается от максимального зна­чения Х_maxна одну единицу младшего разряда (мл. р.):

Для положительных чисел прямой, обратный и дополнительный коды совпадают.

В случае отрицательных чисел дополнительный и обратный коды связаны между собой соотношением:

Правило представления двоичного числа в обратном коде:

1) представить двоичное число в прямом коде в n-разрядном формате. Если число положительное, то его прямой и обратный коды совпадают и больше ника­ких преобразований делать не надо;

2) если число отрицательное, то в старшем (знаковом) разряде надо оставить 1, а в цифровых разрядах все цифры изменить на инверсные, то есть вместо 0 записать 1 и вместо 1 записать 0.

Правило представления двоичного числа в дополнительном коде:

1) представить двоичное число в прямом коде в n-разрядном формате. Если число положительное, то на этом представление числа и заканчивается, так как прямой, обратный и дополнительный коды в этом случае совпадают;

2) если число отрицательное, то перейти от его прямого кода к обратному;

3) прибавить к обратному коду отрицательного числа единицу младшего разряда.

Правило преобразования дополнительного кода в прямой код:

1) если в старшем (знаковом) разряде стоит 0, то число положительное и прямой код совпадает с дополнительным;

2) если в старшем разряде стоит 1, то число отрицательное, поэтому из до­полнительного кода числа надо вычесть 1 младшего разряда с целью получения обратного кода числа, затем заменить все 0 на 1 и 1 на 0 в цифровых разрядах об­ратного кода, а в знаковом разряде оставить 1.

Прямой код из дополнительного кода отрицательного числа можно получить и по-другому: в знаковом разряде оставить 1, все цифровые разряды инвертировать и к полученному проме­жуточному результату прибавить единицу младшего разряда. Дополнительные и обратные коды чисел с фиксированной запятой (точкой) упрощают и ускоряют выполнение арифметических операций в ЭВМ.

Пример 1. Представить в 8-разрядном формате прямые, обратные и дополнительные коды целых двоичных чисел: Х₁ = 1011; Х₂ = –1011; Х₃ = 11 0110; Х₄ = –11 0110. Найти десятичные эквиваленты заданных чисел.

Пример 2. Представить в 8-разрядном формате прямые, обратные и дополнительные коды дробных двоичных чисел, найти их десятичные эквиваленты: Х₁ = –0,11; Х₂ = –0,1101; Х₃ = 0,0101; Х₄ = 0,10101.

Пример 3. Числа представлены как целые в дополнительных кодах: Х₁ =10111101_(доп); Х₂ = 00101010_(доп). Найти десятичные эквиваленты.

Необходимо найти прямые коды чисел, после чего перевести их в десятичные числа.

Число Х₁ отрицательное, следовательно, необходимо перевести его из дополнительного кода в обратный вычитанием одной единицы младшего разряда, затем в прямой код инверсией всех цифровых разрядов и далее в отрицательное двоичное число.

Число Х₂ положительное, следовательно, его прямой код совпадает с дополнительным кодом:

Источник

Представление чисел в ЭВМ

Целые числа

Для числа +1101 :

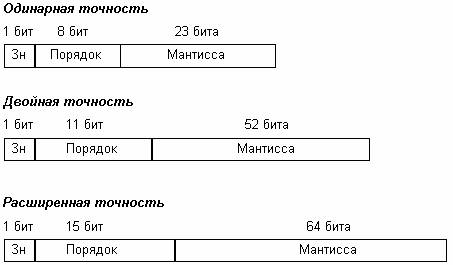
Вещественные числа (числа с плавающей точкой)

0.15625 = 00101₂
446.15625 = 110111110,00101₂ = 1,1011111000101*2 8

Знак S = 0
Порядок P = 8 + 1023 = 1031₁₀ = 10000000111₂
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE28000000000₁₆

455,375 = 111000111,0110₂ = 1,110001110110*2 8 ₂

Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101

1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881

б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011

1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818

Источник

Обратный и дополнительный коды двоичных чисел

Пример перевода
x₁=10101-[x₁]_пр=010101
x₂=-11101-[x₂]_пр=111101
x₃=0,101-[x₃]_пр=0,101
x₄=-0,111-[x₄]_пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.

3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.

Пример перевода
x₁=10101-[x₁]_доп=010101
x₂=-11101-[x₂]_обр=100010+1-[x₂]_доп=100011
x₃=0,101-[x₃]_доп=0,101
x₄=-0,111-[x₄]_обр=1,000+1-[x₄]_доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.

Источник

5. Прямые, обратные и дополнительные коды.

При выполнении арифметических операций в ЭВМ применяют специальные коды для представления чисел (с целью упрощения арифметических операций): прямой, обратный и дополнительный коды чисел.

Прямой код (представление в виде абсолютной величины со знаком) двоичного числа – это само двоичное число, в котором все цифры, изображающие его значение, записываются как в математической записи, а знак числа записывается двоичной цифрой.

Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления, но формат представления чисел в прямом коде неудобен для использования в вычислениях, поскольку сложение и вычитание положительных и отрицательных чисел выполняется по-разному, а потому требуется анализировать знаковые разряды операндов.

Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 – на 0).

Дополнительный код (представление в виде дополнения до двойки) положительного числа совпадает с прямым, а код отрицательного числа образуется как результат увеличения на 1 его обратного кода. Иными словами, процесс построения дополнительного кода отрицательного числа можно разбить на два этапа – построить обратный код, а затем из него построить дополнительный.

Основным достоинством дополнительного кода является то, что в нем единообразно реализуются операции сложения чисел разных знаков, а операцию вычитания можно свести к операции сложения заменой знака вычитаемого на обратный, причем для реализации дополнительного кода, не требуется ни каких дополнительных аппаратных устройств.

6. Представление информации в эвм, числа с фиксированной точкой, плавающей точкой, десятичные числа, символы.

В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц, поэтому компьютер может обрабатывать только информацию, представленную в цифровой форме. Для преобразования числовой, текстовой, графической, звуковой информации в цифровую необходимо применить кодирование. Кодирование – это преобразование данных одного типа через данные другого типа. В ЭВМ применяется система двоичного кодирования, основанная на представлении данных последовательностью двух знаков: 1 и 0, которые называются двоичными цифрами.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной. Эта форма проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки и дальнейшие вычисления теряют смысл. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.(Основной формат и специальный формат)

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Прямой, дополнительный и обратный коды

Прямой, дополнительный и обратный код числа (создан по запросу).

Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.

Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.

Прямой, дополнительный и обратный код

Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен

Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.

Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица

А теперь «зачем, зачем это все?» ©

Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.

С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111

А как представить отрицательные числа?

И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)

Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4

-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6

Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.

Примеры где показаны переносы и пятый разряд

00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение

Два последних переноса 01 — переполнение

-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0

Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.

Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.

Источник