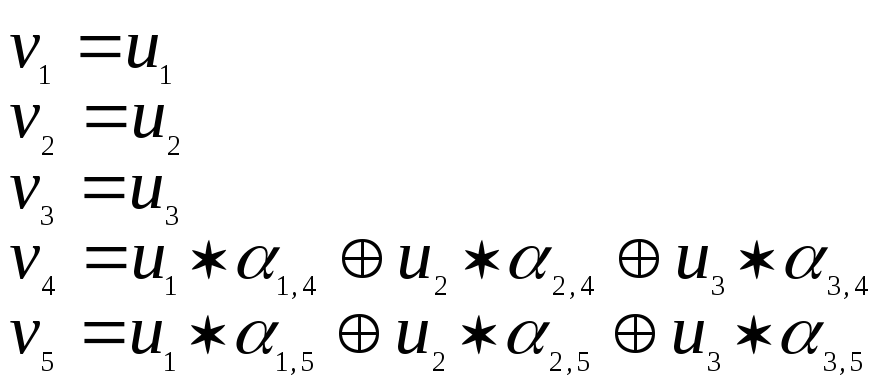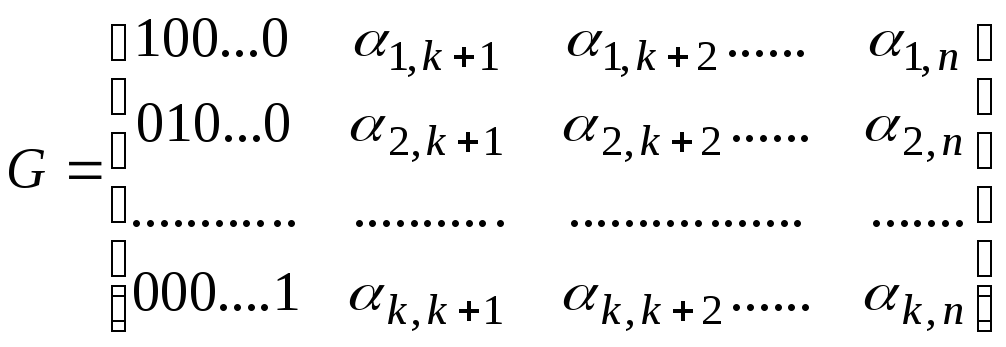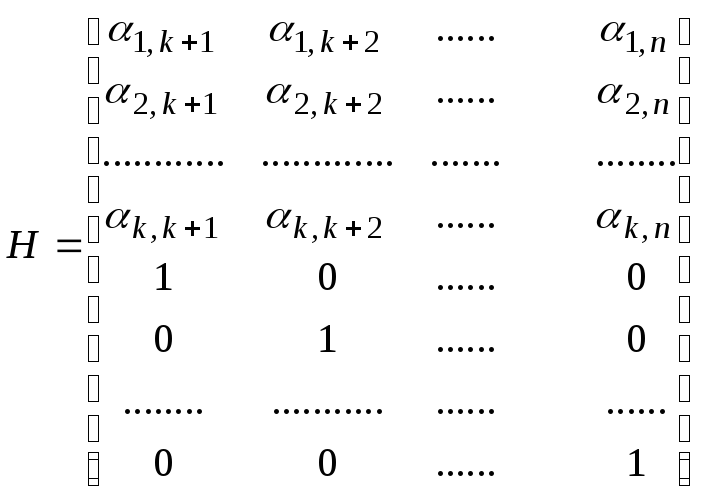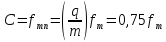мощность линейного кода заданной длины

Цифровая связь — линейные коды

Линейный код — это код, используемый для передачи данных цифрового сигнала по линии передачи. Этот процесс кодирования выбирается таким образом, чтобы избежать наложения и искажения сигнала, таких как межсимвольные помехи.

Свойства линейного кодирования

Ниже приведены свойства линейного кодирования —

Поскольку кодирование выполняется для передачи большего количества битов в одном сигнале, используемая ширина полосы значительно уменьшается.

Для данной полосы пропускания мощность используется эффективно.

Вероятность ошибки значительно снижается.

Обнаружение ошибок сделано, и биполярный также имеет возможность исправления.

Плотность мощности очень благоприятная.

Содержание времени является адекватным.

Длинные строки 1 и 0 избегают, чтобы сохранить прозрачность.

Поскольку кодирование выполняется для передачи большего количества битов в одном сигнале, используемая ширина полосы значительно уменьшается.

Для данной полосы пропускания мощность используется эффективно.

Вероятность ошибки значительно снижается.

Обнаружение ошибок сделано, и биполярный также имеет возможность исправления.

Плотность мощности очень благоприятная.

Содержание времени является адекватным.

Длинные строки 1 и 0 избегают, чтобы сохранить прозрачность.

Типы линейного кодирования

Есть 3 типа линейного кодирования

Униполярный сигнал

Существует две разновидности униполярной сигнализации:

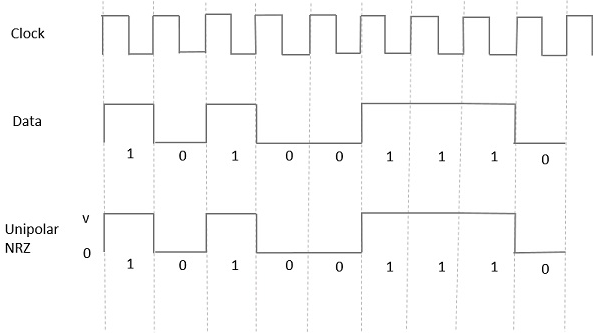
Униполярный невозврат в ноль (NRZ)

Следующий рисунок ясно показывает это.

Преимущества Unipolar NRZ —

Недостатками Униполярного НРЗ являются —

Исправление ошибок не производится.

Присутствие низкочастотных компонентов может привести к снижению сигнала.

Возможна потеря синхронизации (особенно для длинных строк 1 и 0 ).

Исправление ошибок не производится.

Присутствие низкочастотных компонентов может привести к снижению сигнала.

Возможна потеря синхронизации (особенно для длинных строк 1 и 0 ).

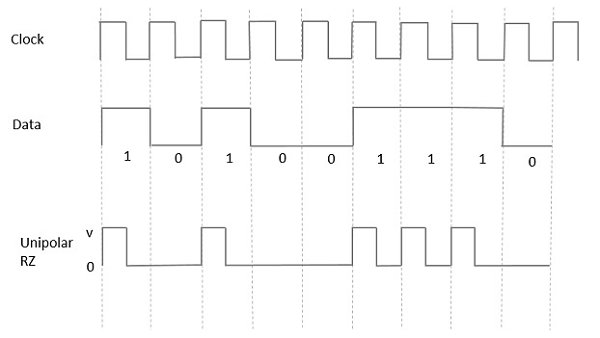
Униполярный возврат в ноль (RZ)

Это ясно понять с помощью следующего рисунка.

Преимущества Unipolar RZ —

Недостатками Unipolar RZ являются —

Полярная Сигнализация

Существует два метода полярной сигнализации. Они —

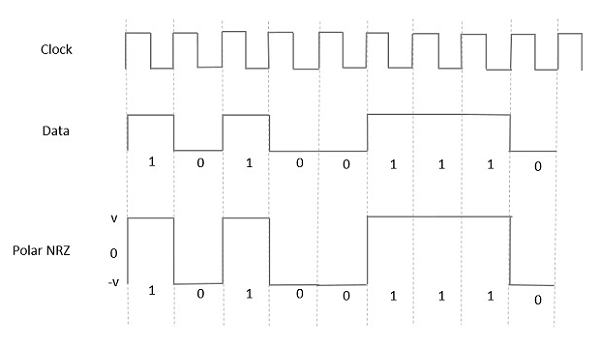
Полярный НРЗ

В этом типе передачи сигналов Polar максимум данных представлен положительным импульсом, а минимум данных представлен отрицательным импульсом. На следующем рисунке это хорошо видно.

Преимущества Polar NRZ —

Недостатками Полярного НРЗ являются —

Нет исправления ошибок.

Нет исправления ошибок.

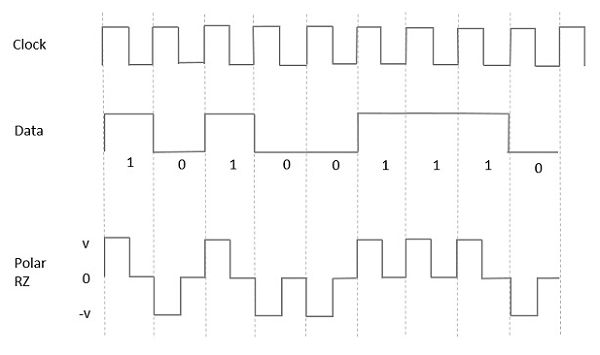
Полярный РЗ

Тем не менее, для входного сигнала Low, отрицательный импульс представляет данные, и нулевой уровень остается тем же самым в течение другой половины битовой длительности. На следующем рисунке это ясно видно.

Преимущества Polar RZ —

Недостатками Polar RZ являются —

Нет исправления ошибок.

Занимает вдвое большую пропускную способность Полярного НРЗ.

Нет исправления ошибок.

Занимает вдвое большую пропускную способность Полярного НРЗ.

Биполярная Сигнализация

Даже в этом методе у нас есть два типа.

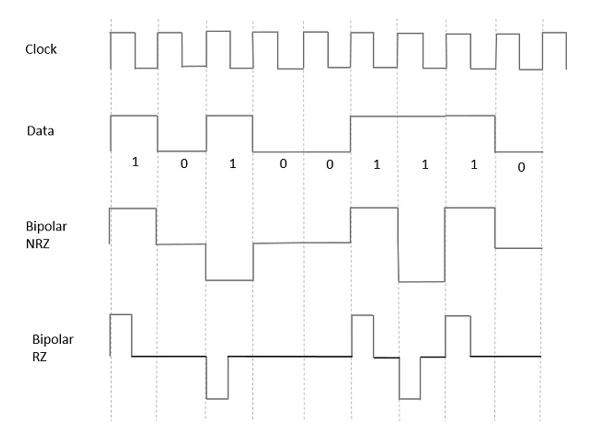
Из моделей, которые мы обсуждали, мы узнали разницу между NRZ и RZ. Здесь тоже все точно так же. Следующий рисунок ясно показывает это.

На приведенном выше рисунке представлены как биполярные сигналы NRZ, так и RZ. Длительность импульса и длительность символа в битах равны в типе NRZ, а длительность импульса составляет половину длительности символа в типе RZ.

преимущества

Ниже приведены преимущества —

Низкочастотных компонентов нет.

Занимает меньшую пропускную способность, чем униполярные и полярные схемы NRZ.

Этот метод подходит для передачи по соединенным линиям переменного тока, поскольку снижение сигнала здесь не происходит.

В этом есть возможность обнаружения одной ошибки.

Низкочастотных компонентов нет.

Занимает меньшую пропускную способность, чем униполярные и полярные схемы NRZ.

Этот метод подходит для передачи по соединенным линиям переменного тока, поскольку снижение сигнала здесь не происходит.

В этом есть возможность обнаружения одной ошибки.

Недостатки

Ниже приведены недостатки —

Спектральная плотность мощности

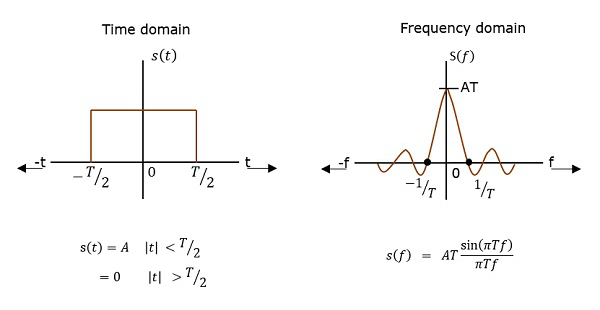
PSD — это Фурье-преобразование автокорреляции (сходство между наблюдениями). Это в форме прямоугольного импульса.

PSD Вывод

Согласно теореме Эйнштейна-Винера-Хинчина, если известна автокорреляционная функция или спектральная плотность мощности случайного процесса, точно можно найти другую.

Отсюда получаем уравнение для спектральной плотности мощности. Используя это, мы можем найти PSD различных линейных кодов.

Источник

Мощность линейного кода заданной длины

Двоичные коды строятся с использованием только двух элементов. В литературе встречаются различные условные обозначения символов двоичного кода. Наиболее употребительные из них рекомендованы МСЭ-Т и представлены в Табл. 6.7.

При реализации кодов необходимо представлять их символы в виде элементов дискретного сигнала той или иной формы, удобной для выполнения последующих операций и передачи по линиям связи.

Формы цифровых сигналов, предназначенных для передачи по линии связи, получили наименование линейных кодов (ЛК). ЛК применяются для передачи данных без модуляции в первичной полосе частот, начинающейся с нуля. Иначе говоря, кадры цифровых систем передачи, сформированные в соответствии с правилами ПЦИ или СЦИ и представляющие собой обычные двоичные последовательности, перед подачей в линию связи подвергаются соответствующему преобразованию в линейном кодере.

Рассмотрим основные типы линейных кодов.

Смысл скремблирования состоит в получении последовательности, в которой статистика появления нулей и единиц приближается к случайной, что позволяет удовлетворять требованиям надежного выделения тактовой частоты и постоянной, сосредоточенной в заданной области частот спектральной плотности мощности передаваемого сигнала.

Заметим, что скремблирование широко применяется во многих видах систем связи для улучшения статистических свойств сигнала. Обычно скремблирование осуществляется непосредственно перед модуляцией.

Особенностью скремблера СС (Рис. 6.52) является то, что он управляется скремблированной последовательностью, т.е. той, которая передается в канал. Поэтому при данном виде скремблирования не требуется специальной установки состояний скремблера и дескремблера; скремблированная последовательность записывается в регистры сдвига скремблера и дескремблера, устанавливая их в идентичное состояние. При потере синхронизма между скремблером и дескремблером время восстановления синхронизма не превышает числа тактов, равного числу ячеек регистра скремблера.

Рис. 6.52. Самосинхронизирующиеся скремблер и дескремблер

Второй недостаток СС скремблера связан с возможностью появления на его выходе при определенных условиях так называемых критических ситуаций, когда выходная последовательность приобретает периодический характер с периодом, меньшим длины ПСП. Чтобы предотвратить это, в скремблере и дескремблере согласно рекомендациям МСЭ-Т предусматриваются специальные дополнительные схемы контроля, которые выявляют наличие периодичности элементов на входе и нарушают ее.

Рис. 6.50. Аддитивные скремблер и дескремблер

Суммируемые в скремблере последовательности независимы, поэтому их период всегда равен наименьшему общему краткому величин периодов входной последовательности и ПСП и критическое состояние отсутствует. Отсутствие эффекта размножения ошибок и необходимости в специальной логике защиты от нежелательных ситуаций делают способ аддитивного скремблирования предпочтительнее, если не учитывать затрат на решение задачи фазирования скремблера и дескремблер. В качестве сигнала установки в ЦСП используют сигнал цикловой синхронизации.

Источник

ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ

Теория кодирования. Линейные блоковые коды.

Разработать программный модуль, который по заданным параметрам
(n, k, d) строит двоичный линейный блоковый код.

Требования к программе:

2. Ход исследования

2.1. Краткие теоретические сведения

Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Блоковый код, соответствующий данным параметра, обычно обозначают (n, k). Также вводится определение числа R = n / k, называемое скоростью кода.

Число d называется минимальным расстоянием кода, определяющееся, как минимум расстояния Хэмминга по всем возможным парам различных кодовых слов.

Корректирующей способностью (error correcting capability) t кода C называют максимальное количество ошибок, которое можно обнаружить с данными параметрами: t = (d-1)/2, округленное вниз.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:

Таким образом, требуется обеспечить: d0 ↑, N ↑, n ↓.

Очевидно, что приведённые требования противоречат друг другу. Именно поэтому кодов существует достаточно много.

Верхняя граница N_В определяется утверждением: не существует кода, число слов в котором N>N_В.

Нижняя граница N_Н определяется утверждением: существует код, число слов в котором N>=N_Н.

Произвольная порождающая матрица G линейного блокового (n,k,d) кода может быть преобразована к систематическому (каноническому) виду с помощью элементарных операций и перестановок столбцов матрицы.

Матрица G_sys состоит из двух подматриц: единичной матрицы I_k размерами k*k и k*(n-k) проверочной подматрицы P (матрица дополнений). Таким образом, G_sys=(I_k|P).

Для построения линейного блокового кода достаточно найти матрицу дополнений P. Матрица P состоит из k векторов длины r=n-k.

Исходя из того, что все векторы в матрице P различны, и того, что перестановка векторов будет давать эквивалентную порождающую матрицу, будем строить матрицу дополнений следующим образом:

Если нам удалось найти по такому принципу векторов, мы нашли код с заданными параметрами. Можем выйти из алгоритма или перейти на предыдущий шаг для поиска других кодов с такими же параметрами.

Если k векторов найти не удалось, увеличим n на единицу, создадим заново множество А. Тем самым будем рассматривать векторы, отобранные ранее, в новом пространстве с увеличенным числом измерений, считая у них нулевой координату нового измерения.

Увеличивая n, мы либо построим на каком-то шаге матрицу дополнений, либо n достигнет нижней границы Варшамова–Гильберта, код с таким n удовлетворяет требуемым параметрам, следовательно, матрица будет построена.

Источник

Линейные коды

Блочным линейным кодом называется (n, k) код, проверочные символы которого являются линейными комбинациями информационных символов. Здесь:

n – длина кода, то есть длина кодовых слов

k – число информационных символов

Обозначим U – последовательность из k информационных символов.

Обозначим V – кодовое слово линейного кода длиной n символов.

К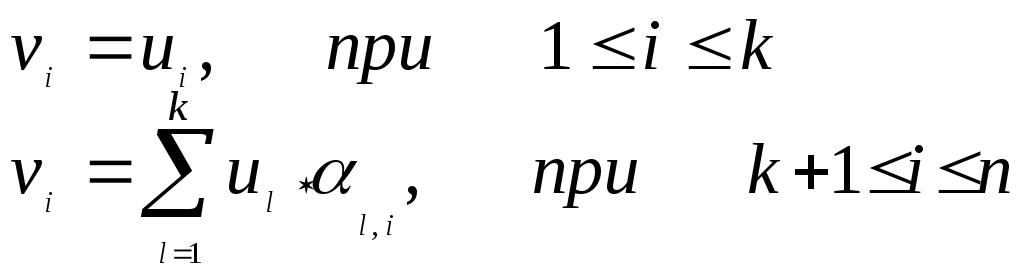одовое словоV формируется из информационной последовательности U по следующему правилу:

Отношение R=k/n называется скоростью кода, а величина W=1-R – называется избыточностью кода.

Запишем в виде формул процедуру нахождения символов кодового слова для линейного кода с параметрами (5, 3), если задана некоторая информационная последовательность из трех символов U=(u₁,u₂,u₃). Кодовое слово будет содержать 5 символов V=(v₁,v₂,v₃,v₄,v₅).

Это запись образующей матрицы в канонической форме.

Кодовая комбинация на выходе кодера канала равна произведению информационной последовательности на образующую матрицу линейного кода V=U×G.

Свойства линейных кодов

Любые к линейно-независимых кодовых слов задают все множество 2 к слов линейного кода.

К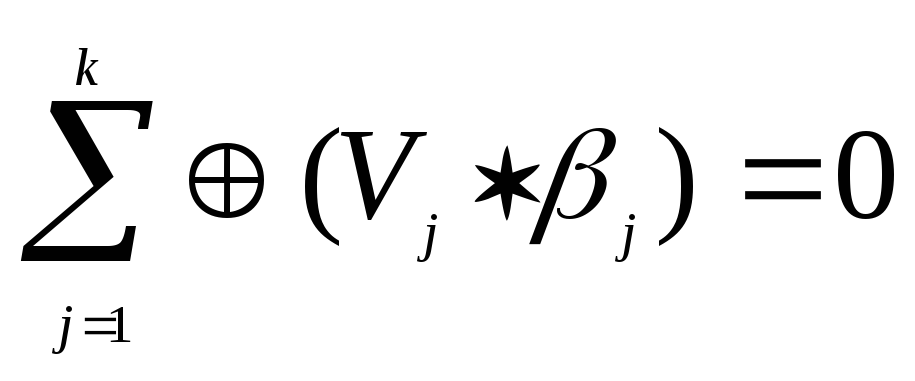одовые словаV_j являются линейно-независимыми, если сумма по модулю 2, приведенная ниже, равна 0 только, когда все двоичные коэффициенты _j равны 0.

Другими словами: суммирование любого числа кодовых слов из группы k линейно-независимых слов Vj не приводит к нулевому результату.

Сумма по модулю 2 любого числа кодовых слов также является словом данного линейного кода.

Нулевая последовательность всегда является кодовым словом.

Кодовое расстояние d_min равно минимальному весу ненулевого кодового слова.

Из любого линейного (n,k) кода с кодовым расстоянием d_min можно получить укороченный код (n-i, k-i) с кодовым расстоянием не меньше d_min.

Декодирование линейных кодов

Обозначим последовательность, поступающую с выхода дискретного канала на вход декодера Y. Процедура декодирования линейного разделимого кода сводится к проверке соотношения: принятые проверочные элементы кодовой комбинации совпадают с результатом вычисления этих элементов принимающей стороной? Для проверки этого соотношения декодер вычисляет синдром принятой последовательности.

Синдром S – это строка, которая содержит r=n—k элементов и представляет собой сумму  (по модулю 2) для каждого из r проверочных символов, вычисленных по принятым информационным символам, и r реально принятых проверочных символов.

Если ошибки в принятой комбинации отсутствуют, синдром равен нулю S=0 (все элементы синдрома равны 0). Если принятый j-й проверочный символ (1 k векторам ошибок.

Если 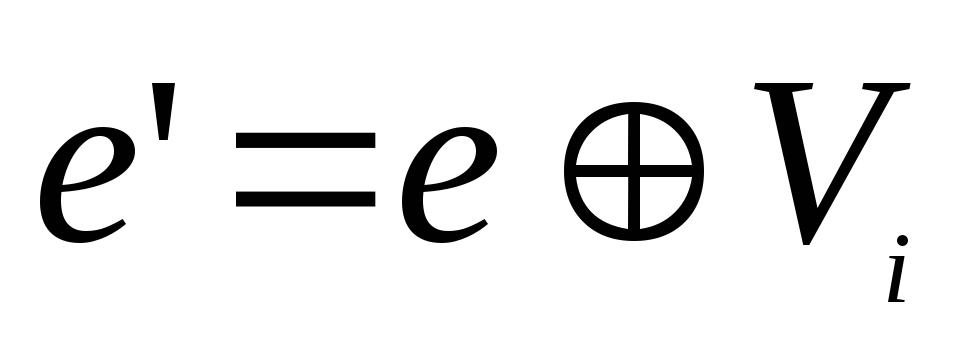, то вектор ошибки e‘ имеет тот же синдром, что и вектор e.

Синдром может быть вычислен с использованием проверочной матрицы Н.

Проверочная матрица имеет размерность n×r. Первые k строк проверочной матрицы представляют собой совокупность коэффициентов α_li, остальные r строк – это единичная матрица размером r×r.

Для кода (5,3) с образующей матрицейG

проверочная матрица имеет вид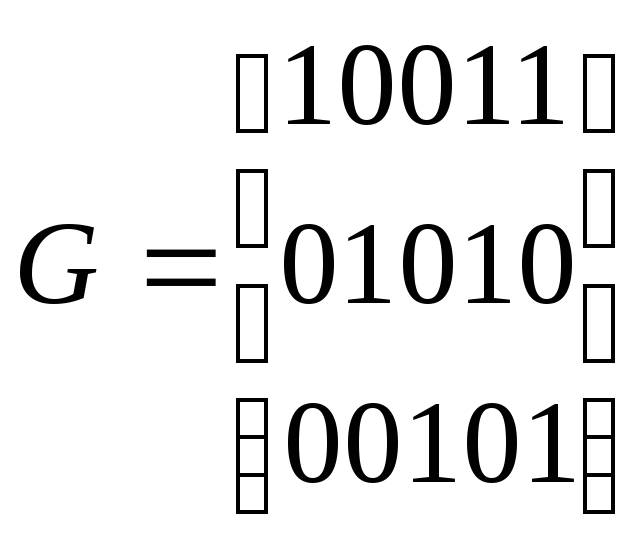

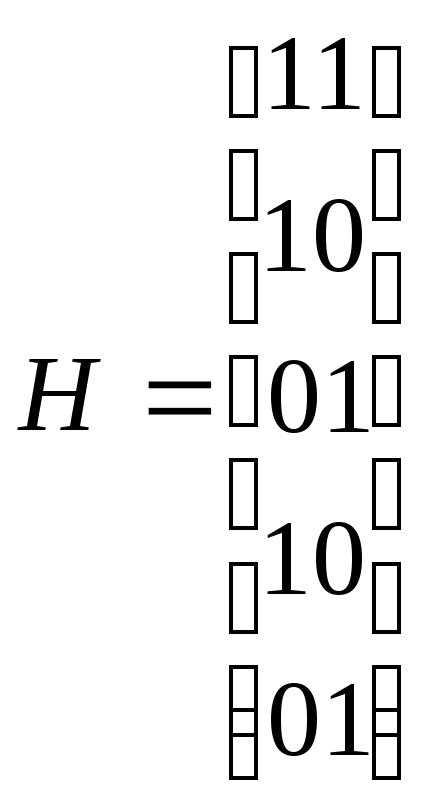
Декодирование с обнаружением ошибок

В данном случае при приеме последовательности Y вычисляется синдром S. Если S не равен нулю, выдается сигнал наличия ошибки. Если вектор ошибки e совпадает с одним из кодовых слов, ошибка не может быть обнаружена.

Определим вероятность необнаруженной ошибки при передаче комбинаций по каналу с независимыми ошибками (ДСК без памяти):

Д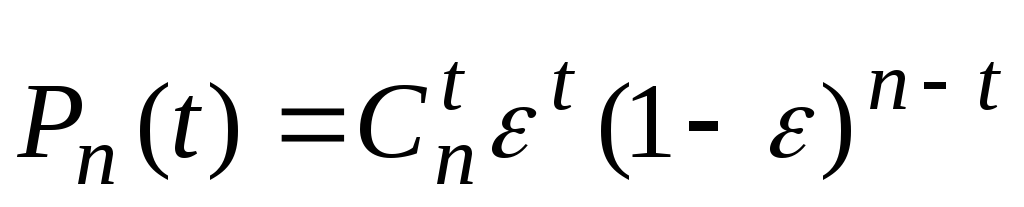л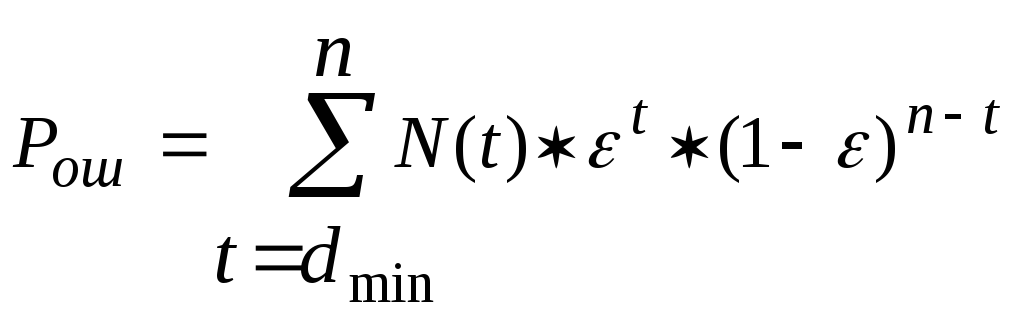я ДСК без памяти вероятность появлениялюбого вектора ошибок веса t в кодовом слове длиной n символов равна

Линейный код не обнаружит ошибку, если вектор ошибки совпадет с каким-либо кодовым словом. Поэтому, для вычисления вероятности необнаруженной ошибки необходимо знать спектр весов кода. Спектром весов кода называется последовательность чисел N(t), каждое из которых показывает число кодовых слов, содержащих t единиц.

Декодирование с исправлением ошибок

При декодировании с исправлением ошибок каждому синдрому линейного кода ставят в соответствие определенный вектор ошибки, который является наиболее вероятным в заданном канале. Например, если задан двоичный симметричный канал без памяти ДСК, то в таблицу декодирования линейного кода следует включить вектора ошибок с минимальным весом.

Задан код с длиной кодового слова n=12. Определить необходимое минимальное число проверочных символов, если код должен исправлять все одиночные ошибки?

Я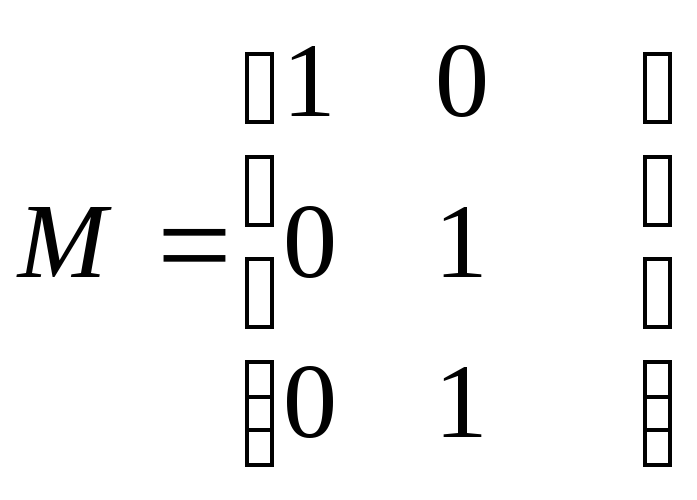вляются ли принятые последовательности кодовыми словами данного кода:

Источник

6.2. Линейные коды

Линейный цифровой сигнал (ЛЦС), формируемый на основе ли­нейного кода, должен отвечать следующим требованиям.

Структура ЛЦС должна быть такой, чтобы можно было просто и надежно выделить тактовую частоту в каждом линейном регенераторе и на оконечной станции.

3. Должна быть обеспечена возможность постоянного и достаточно простого контроля коэффициента ошибок в линейном тракте без перерыва связи.

4.Уменьшения при необходимости тактовой частоты передавае­мого сигнала по сравнению с ИКМ сигналом.

5. Используемые линейные коды не должны приводить к существенному размножению ошибок и иметь достаточно простую аппаратную реализацию.

Для минимизации постоянной составляющей в спектре ЛЦС необхо­димо, чтобы на любом интервале времени T_и алгебраическая сумма по­следовательных значений появляющихся за это время символов линейно­го кода (цифровая сумма) была минимальной, т. е.

(6.2)

Где — i-е значение символа в момент времени t. Очевидно, что для выполнения указанного требования в коде примерно с одинаковой веро­ятностью должны появляться импульсы противоположной полярности.

Поскольку на вероятность появления двоичных символов ИКМ сигна­ла практически не могут быть наложены ограничивающие условия, то для удовлетворения отмеченным требованиям линейный код должен обладать некоторой избыточностью. Избыточность в ЛЦС можно, например, полу­чить, если при формировании линейного кода использовать число уров­ней сигнала больше двух. При n-уровневом линейном коде число переда­ваемых состояний за единицу времени будет больше числа возможных состояний за то же время в двоичном коде, т.е. выполняется неравенство

(6.3)

Очевидно, что при формировании линейного кода должно выполнять­ся условие

(6.4)

Где — длительности символов и-уровневого и двоичного кода соответственно.

С учетом (6.3) и (6.4) нетрудно получить следующее соотношение ме­жду скоростью передачи в ЦЛТ f_тп и скоростью передачи исходного ИКМ сигнала

(6.5)

Последнее выражение может быть записано также в следующем виде (6.6)

В свою очередь, избыточность линейного кода в случае необходимости может быть оценена с помощью соотношения, вытекающего из (6.5) и (6.6) (6.7)

С целью повышения стабильности признаков тактовой частоты для большинства двоичных ИКМ сигналов требуется дополнительное преоб­разование ИКМ сигнала путем изменения его статистических свойств. Если изменение статистических свойств исходного ИКМ сигнала проис­ходит при некоторых определенных условиях (например, заданном количестве подряд следующих 0), то в результате формируются так называе­мые неалфавитные коды.

Если же статистические свойства исходного ИКМ сигнала изменяются путем деления на группы с постоянным числом тактовых интервалов и последующего преобразования этих групп по определенному алфавиту в группы символов кода с другим основанием (больше двух), и, как прави­ло, с новым количеством тактовых интервалов, то в результате формиру­ются алфавитные коды.

Для линейных трактов ЦСП, использующих электрические кабели, ос­новные типы кодов и соответствующие им линейные цифровые сигналы показаны на рис. 6.3.

Рис. 6.3. Линейные коды цифровых систем передачи по электрическим кабелям

На рис. 6.3,а приведена случайная реализация цифрового ИКМ сигнала на выходе формирователя или оборудования временного группообразования (мультиплексирования).

Этот двоичный (ДВС) сигнал представляет случайную однополярную последовательность символов 1 и 0, энергетический спектр которой описы­вается выражением (6.1).

На рис. 6.3,6 представлен абсолютный биимпульсный сигнал (АБС). При формировании кода АБС вместо каждой единичной посылки исход­ного ДВС длительностью передается двухполярная посылка вида (+/-) длительностью а вместо каждой нулевой посылки исходного ДВС передается двухполярная посылка вида (-/+) длительностью также Сигналы вида (+/-) и (-/+) называютсябиимпульсными и обладают важ­ными достоинствами: высокая помехозащищенность, простота преобра­зования двоичного сигнала в биимпульсный, возможность выделения так­товой частоты вне зависимости от статистических свойств исходного ДВС, возможность использования пороговых устройств в линейных реге­нераторах с пороговым напряжением, равным нулю. Однако частота сле­дования биимпульсного сигнала практически приводит к увеличению вдвое тактовой частоты ЛЦС.

Рис. 6.4. К формированию кода ЧПИ

не требуется. При обратном преобразовании просто определяется состоя­ние сигнала в предыдущем интервале: если произошло изменение, то фиксируется 1, в противном случае фиксируется 0.

Энергетический спектр сигнала ЧПИ при равной вероятности появления 1 и 0 в исходном ДВС определяется по формуле

(6.8)

Анализ формулы (6.8) показывает, что у квазитроичного сигнала отсут­ствует не только постоянная составляющая, но и вообще вся дискретная часть спектра, а энергия его непрерывной части сконцентрирована в облас­ти частот, близких к половине тактовой частоты f_т/2 (рис. 6.4,а). Преобразо­вание исходного ДВС в квазитроичный код с ЧПИ осуществляется в преоб­разователе кода, схема которого (схема Баркера) приведена на рис. 6.4,б.

Триггер Тг_, на счетный вход которого поступает ДВС, при поступлении очередной 1 меняет свое состояние на обратное. Выходы триггера соедине­ны с входами логических элементов И₁ и И₂; на вторые входы этих схем подается исходный ДВС. Переключения триггера приводят к тому, что схе­мы И открываются поочередно.

В соответствии с их состоянием происходит запуск соответствующих блокинг-генераторов (БГ₁ или БГ₂), находящихся в ждущем режиме. Блокинг-генераторы формируют импульсы с заданными параметрами, а благо­даря использованию выходного трансформатора (Тр) со средней точкой полярность выходных импульсов, поступающих от каждого плеча схемы, оказывается различной, т.е. создается квазитроичный сигнал с ЧПИ. Для обратного преобразования сигнала с ЧПИ в ДВС необходима схема, экви­валентная двухполупериодному выпрямителю.

Другой вариант преобразования ДВС в сигнал с ЧПИ представлен на рис. 6.5.

Работа схемы поясняется временными диаграммами (рис. 6.6). Исход­ный ДВС (рис. 6.6,а) поступает на сумматор по модулю 2 <mod 2).Ha другой вход сумматора поступает сигнал, прошедший через линию задержки ЛЗ₁ и задержанный на один тактовый интервал Т (рис. 6.6,в). Сигнал с выхода сумматора (рис. 6.6,6) поступает на вычитающее устройство (ВУ). Этот же сигнал, задержанный линией задержки ЛЗ₂ на интервал Т (рис. 6.6,г), посту­пает на другой вход ВУ.

На выходе ВУ формируется квазитроичный сигнал в коде ЧПИ (рис. 6.6,(3). Достоинством кода ЧПИ является простота его формирования на передаче и декодирования на приеме. Энергетический спектр кода ЧПИ не содержит постоянной составляющей, и концентрация основной энергии происходит в области полутактовой частоты (0,5 f_т) исходной двоичной последовательности (рис. 6.4,а).

Избыточность кода ЧПИ определим по формуле (6.7), имея в виду, что

Рис. 6.5. Формирователь кода ЧПИ с использованием линий задержки

Рис. 6.6. Временные диаграммы работы схемы рис. 6.5

один символ исходного двоичного кода преобразуется в один символ ква­зитроичного или трехуровневого кода (п = 3), т.е. m = 1 и q = 1. Подставив в (6.7) значения величин л = 3, q= 1,/я=1 для кода ЧПИ, получим избыточ­ность Указанная избыточность достаточно велика и поэтому допускает большую свободу в выборе принципов построения линейных кодов, удовлетворяющих вышеперечисленным требованиям к ЛЦС.

От вышеуказанных недостатков в некоторой степени свободны моди­фицированные коды ЧПИ (МЧПИ), также называемые кодами с высокой плотностью единиц порядка N (КВП-ЛО или HDB-N (High Density Bipolar of order N), в которых повышена вероятность формирования им­пульсов по сравнению с исходным двоичным сигналом.

В табл. 6.1 (и ранее) через V обозначается символ, полярность которо­го повторяет полярность предыдущего символа В, полярность которого изменяется по закону кода ЧПИ. Использование двух замещающих после­довательностей обеспечивает чередование полярности символов V, появ­ляющихся в различных местах ЛЦС, что, в свою очередь, позволяет уст­ранить влияние этих символов на среднее значение, которое так же, как и у кода ЧПИ, оказывается равным нулю. Однако цифровая сумма кода HDB-3 (6.2) из-за введения символов V оказывается большим, чем для кода с ЧПИ, и может составлять 2(+1/2) или 2(-1/2).

При использовании кода HDB-3 существенно сокращается диапазон изменения вероятности появления единичных символов в ЛЦС, который ограничивается пределами в то время как в коде с ЧПИ эта вероятность практически может уменьшаться до нуля. Следовательно, при использовании кода HDB-3 существенно улучшаются условия работы устройств выделения тактовой частоты. Энергетический спектр кода HDB-3 подобен энергетическому спектру кода ЧПИ.

Код HDB-3 является основным в первичной, вторичной и третичной ЦСП ИКМ-ВРК, работающих по металлическим кабелям. Кроме того, он широко применяется как стыковой код в оконечной аппаратуре при со­единении разных иерархических структур.

Для формирования кода HDB-3 требуется некоторое усложнение схем (рис. 6.4,6 и 6.5), вызванное необходимостью контроля за количеством нулей между единицами ДВС и формированием выходных символов V, нарушающих правило чередования полярности импульсов.

На рис. 6.3,з приведен так называемый парно-избирательный троич­ный (ПИТ) код, где символы передаваемой двоичной последовательности группируются попарно и преобразуются в троичный сигнал в соответствии с табл. 6.2 кодирования.

Энергетический спектр ЛЦС на основе кода ПИТ близок к энергетиче­скому коду сигнала с ЧПИ. Это означает, что максимум энергии находит­ся в середине полосы, и с этой точки зрения линейные тракты для кода ПИТ (а также HDB-3 и B3ZS) не отличаются по величине достижимого от­ношения сигнал-шум (ОСШ). Недостатком рассмотренного типа ЦЛС явля­ется необходимость синхронизации по парам символов исходного ДВС.

т.е. меньше скорости передачи кодов типа 1В1Т (коды ЧПИ, HDB-3. ПИТ); при этом снижается затухание кабеля на тактовой частоте f_тп, что позволяет увеличить ОСШ либо увеличить длину регенерационного участка.

Избыточность таких кодов согласно (6.7) равна

Следовательно, имеются возможности наложения некоторых дополни­тельных условий на линейный код с целью приспособления его свойств к параметрам линейного тракта. В процессе формирования кодов типа mBqT используется несколько вариантов алфавитов, выбор кон­кретного из них осуществляется на основе анализа числа предшествую­щих символов с учетом структуры исходной последовательности. Сле­довательно, одна и та же группа исходных двоичных символов может быть представлена различными группами кода 4ВЗТ. Выбор комбинаций выполняется по требованиям, аналогичным требованиям к коду типа ПИТ (табл. 6.3).

Соответствующая последовательность квазитроичного кода выбирает­ся таким образом, чтобы минимизировалась цифровая сумма. При этом счетчик, подсчитывающий текущее значение цифровой суммы, принима­ет решение о посылке в линию одной из последовательностей, приведен­ных в столбцах I, II, III и IV (табл. 6.3). Синхронизация процесса преобра­зования линейного кода в код ДВС в приемном оборудовании осуществ­ляется путем контроля цифровой суммы и выявления последовательно­стей, не используемых при преобразовании на передаче, например 000.

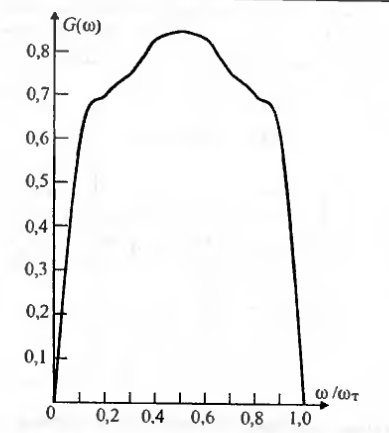
Энергетический спектр кода 4ВЗТ представлен на рис. 6.7, из которого следует, что максимум спектра сосредоточен в середине полосы, как и для кодов ЧПИ, HDB-3 или ПИТ. Однако следует обратить внимание, что для кода 4ВЗТ эта полоса на 25% хуже.

Многоуровневые коды. В тех случаях, когда полоса линейного тракта ограничена, но необходимо увеличить скорость передачи информации, можно увеличить число уровней. В многоуровневой системе скорость пере­дачи двоичных сигналов

Скорость передачи сигналов, численно равную 1/Г, часто называют ско­ростью передачи символов я измеряют в водах. Среди специалистов в об­ласти передачи данных слово бод обычно принято использовать как синоним скорости передачи двоичных символов. Однако, строго говоря, скорость пере-

Рис. 6.7. Энергетический спектр кода 4ВЗТ

дачи двоичных символов равна скорости передачи в бодах только в том слу­чае, когда осуществляется передача сигнала 1 бит на тактовый интервал.

На рис. 6.8. показан пример восьмиуровневого сигнала, при котором достигается передача трех битов на тактовый интервал (т.е. трех битов на бод).

Системы с передачей многоуровневых сигналов обеспечивают более высокую скорость передачи двоичных символов в пределах заданной по­лосы, но требуют существенного увеличения отношения сигнал-шум при

Рис. 6.8. Многоуровневая передача с тремя битами на тактовый интервал

Источник