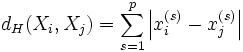найдите расстояние хэмминга между двоичными кодами 001101 и 101011
Расстояние Хемминга
Расстояние Хэмминга — мера (точнее, метрика) различия объектов одинаковой размерности.
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга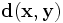 
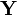
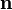
между двумя двоичными последовательностями (векторами) 
и 
длины 
называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в Словарь алгоритмов и структур данных Национального Института Стандартов США (англ. NIST Dictionary of Algorithms and Data Structures ).
Так, расстояние Хэмминга между векторами 0 01 1 1 и 1 01 0 1 равно 2 (красным отмечены различающиеся биты). В дальнейшем метрика была обобщена на q-ичные последовательности: для пары строк « вы бор ы » и « за бор а » расстояние Хэмминга равно трём.
В общем виде расстояние Хэмминга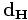 
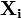
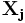
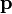
для объектов 
и 
размерности 
задаётся функцией:
Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:
Содержание
Расстояние Хэмминга в биоинформатике и геномике
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.
Родственные методы
Литература
Ссылки
Полезное
Смотреть что такое «Расстояние Хемминга» в других словарях:
расстояние Хемминга — хемминговское расстояние Расстояние d (u,v) между двумя кодовыми последовательноаями u и v одинаковой длины, равное числу символов, в которых они отличаются. Блочный код с минимальным хемминговским расстоянием d позволяет обнаружить (d 1) и… … Справочник технического переводчика
кодовое расстояние — Минимум расстояния Хемминга, взятый по всем ларам различных кодовых слов в равномерном коде. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория… … Справочник технического переводчика
Линейный код — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Порождающая матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Проверочная матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Обнаружение и исправление ошибок — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления… … Википедия
Избыточное кодирование — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Избыточность данных — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Исправляющие ошибки Коды — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Коды, исправляющие ошибки — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Расстояние Хэмминга
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга 
между двумя двоичными последовательностями (векторами) 
и 
длины 
называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures ). Расстояние Хэмминга является частным случаем метрики Минковского:
.
Примеры
Свойства
Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:
Расстояние Хэмминга в биоинформатике и геномике
Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.
См. также
Примечания
Литература
Полезное
Смотреть что такое «Расстояние Хэмминга» в других словарях:
расстояние Хэмминга — Число позиций, в которых два слова одинаковой длины отличаются друг от друга. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория передачи… … Справочник технического переводчика
Расстояние Хемминга — Расстояние Хэмминга мера (точнее, метрика) различия объектов одинаковой размерности. Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными … Википедия
Расстояние Левенштейна — (также редакционное расстояние или дистанция редактирования) между двумя строками в теории информации и компьютерной лингвистике это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на… … Википедия
Расстояние кода — в теории кодирования метрики отличий кодов. Наиболее используемыми расстояниями являются: Расстояние Хэмминга Расстояние Левенштейна Расстояние Йенцена Шаннона См. также Объём кода Граница кода … Википедия
Код Хэмминга — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Медаль Ричарда Хэмминга — (англ. Richard W. Hamming Medal) награда, присуждаемая ежегодно институтом инженеров электротехники и электроники (англ. IEEE) за исключительный вклад в науку об информации, информационные системы и технологии. К награде могут… … Википедия
Хэмминг, Ричард Уэсли — Ричард Уэсли Хэмминг Richard Wesley Hamming Дата рождения: 11 февраля 1915(1915 02 11) Место рождения: Чикаго, Иллинойс Дата смерти … Википедия
Неравенство Гильберта-Варшамова — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе неравенство Варшамова … … Википедия
Неравенство Гильберта — Варшамова — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе … … Википедия
Неравенство Варшамова-Гильберта — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе неравенство Варшамова … … Википедия
Подсчет расстояния Хэмминга на большом наборе данных
Введение
Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.
Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.
Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.
Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.
Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.
Описание проблемы
Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.
Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.
В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.
— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.
В статье описывается решение только статической задачи.
Описание алгоритма HEngine для статической задачи
Данная реализация фокусируется на поиске строк в пределах k = ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) = ⌊k/2⌋ + 1
Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.
Теперь тоже самое, только на примере:
Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.
Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1
Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.
И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.
Предварительная обработка базы данных
Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).
Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.
Но как производить поиск по подстрокам?
Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).
В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:
Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2
Затем эти таблицы сигнатур сортируются.
Реализация поиска
На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.
Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.
Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).
Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.
А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.
Такие действия надо произвести для всех подстрок и для всех таблиц.
И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111
Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111
На этом предварительная обработка закончена. И приступаем к поиску.
1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.
2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.
2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010
2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101
3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Найдено две подстроки.
3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.
1100
0100
1000
1110 == 1110 => 00111110
1101
Найдена одна подстрока.
4. Объедением результаты в один список:
00111110
11111111
5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию
Расстояние Хэмминга между двумя струнами
Вам даны две строки одинаковой длины, вы должны найти расстояние Хемминга между этими строками.
Где расстояние Хэмминга между двумя строками одинаковой длины — это число позиций, в которых соответствующие символы различны.
Эта проблема может быть решена простым подходом, при котором мы пересекаем строки и считаем несоответствие в соответствующей позиции. Расширенная форма этой проблемы — редактирование расстояния.
Ниже приведена реализация двух строк.
// C ++ программа для поиска расстояния Хэмминга ч / б
// две строки
#include
using namespace std;
// функция для вычисления расстояния Хэмминга
int hammingDist( char *str1, char *str2)
char str1[] = «geekspractice» ;
char str2[] = «nerdspractise» ;
// Java-программа для определения расстояния Хэмминга
// ч / б две строки
<
// функция для вычисления расстояния Хэмминга
static int hammingDist(String str1, String str2)
public static void main (String[] args)
String str1 = «geekspractice» ;
String str2 = «nerdspractise» ;
System.out.println(hammingDist (str1, str2));
// Этот код предоставлен Anant Agarwal.
// C # программа для поиска Хэмминга
// расстояние ч / б две строки
// функция для расчета
// расстояние Хэмминга
static int hammingDist(String str1,
public static void Main ()
String str1 = «geekspractice» ;
String str2 = «nerdspractise» ;
// Этот код предоставлен нитин митталь
// PHP программа для поиска расстояния Хэмминга ч / б
// две строки
// функция для расчета
// расстояние Хэмминга
// Этот код предоставлен нитин митталь.
?>
Временная сложность: O (n)
Примечание. Для расстояния Хэмминга двух двоичных чисел мы можем просто вернуть количество установленных бит в XOR двух чисел.
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
Расстояние Хэмминга
Из Википедии, бесплатной энциклопедии
d i j = ∑ k = 1 p | x i k − x j k | <\displaystyle d_
\left|x_
.
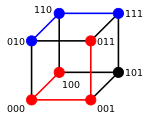
Два слова, расстояние Хэмминга между которыми равно 1, называют соседними.
В некоторых системах счисления, например, в коде Грея, целые кодированные числа, различающиеся на 1, имеют расстояние Хэмминга равное 1. Говорят, что такие числа являются «соседними».
Соседнее кодирование важно при проектировании логических устройств, где необходимо исключить логические гонки.
Примеры [ править | править код ]
Свойства [ править | править код ]
Расстояние Хэмминга всегда:
Расстояние Хэмминга в биоинформатике и геномике [ править | править код ]
Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.