найти расстояние хемминга для следующих кодов

Подсчет расстояния Хэмминга на большом наборе данных

Введение

Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.

Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.

Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.

Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.

Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.

Описание проблемы

Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.

Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.

В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.

— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.

В статье описывается решение только статической задачи.

Описание алгоритма HEngine для статической задачи

Данная реализация фокусируется на поиске строк в пределах k = ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) = ⌊k/2⌋ + 1

Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.

Теперь тоже самое, только на примере:

Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.

a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001

Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.

Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1

Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.

И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.

Предварительная обработка базы данных

Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).

Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.

Но как производить поиск по подстрокам?

Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).

В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:

Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2

Затем эти таблицы сигнатур сортируются.

Реализация поиска

На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.

Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.

Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).

Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.

А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.

Такие действия надо произвести для всех подстрок и для всех таблиц.

И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) 11111111
1000 0001 => 10000001
0011 1110 => 00111110

4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111

Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111

На этом предварительная обработка закончена. И приступаем к поиску.

1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.

2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.

2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010

2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101

3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.

1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010

Найдено две подстроки.

3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.

1100
0100
1000
1110 == 1110 => 00111110
1101

Найдена одна подстрока.

4. Объедением результаты в один список:
00111110
11111111

5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию

Источник

Расстояние Хэмминга

Расстояние Хэмминга используется для обнаружения и исправления ошибок путем сравнения единиц данных, полученных по каналу передачи, с действительными символами. Любая коррекция персонажей основана на принципе вероятности. Возможность обнаружения или исправления ошибок зависит от расстояния Хэмминга.

Содержание

определение

Следует отметить, что расстояние Хэмминга также является метрикой в кодовом пространстве.

Примеры

001 1 0 и 001 0 0	→ расстояние Хэмминга = 1
1 2 34 5 и 1 3 34 4	→ расстояние Хэмминга = 2
Н ая с и B Au м	→ расстояние Хэмминга = 2

Вес Хэмминга

Расстояние Хэмминга кода

Наименьшее из трех расстояний равно 1, поэтому расстояние Хэмминга кода также равно 1.

Расстояние Хэмминга важно, если вы хотите разработать коды, которые позволяют обнаруживать ошибки ( EDC ) или исправлять ( ECC ).

Нахождение расстояния Хэмминга кода

Диаграмма Карно-Вейча

4-й	3	2	3	4-й
3	2	1	2	3
2	1	Икс	1	2
3	2	1	2	3
4-й	3	2	3	4-й

Пример применения

При передаче данных необходимо убедиться, что информация не фальсифицирована или что изменения в данных, по крайней мере, заметны (обнаружение n-кратных ошибок) и, возможно, могут быть исправлены.

В следующем примере поворотный переключатель имеет четыре варианта настройки. Они передаются получателю в электронном виде в виде двоичного числа (кодового слова): 00, 01, 10, 11; Приемник получает кодовое слово, но не имеет других средств проверки или распознавания положения переключателя. В технических приложениях это уже тот случай, когда приемник представляет собой микроконтроллер, а передатчик состоит из датчиков внутри переключателя.

В этом сценарии приемник не имеет возможности распознать нарушение передачи или дефект в переключателе (например, неисправные датчики в переключателе). С помощью расстояния Хэмминга и соответствующих кодов можно найти способ обнаружения ошибок в передатчике или в линии.

Расстояние Хэмминга между четырьмя упомянутыми значениями 00, 01, 10, 11 в каждом случае равно 1, т.е. ЧАС. если из-за ошибки инвертируется только один бит, приемник получит другое, но одинаково действительное кодовое слово. Если от 00 до 01 фальсифицировано, получатель не может распознать ошибку только по сообщению, потому что и предполагаемое, и фальсифицированное значение описывают допустимое положение переключателя.

В случае единственного ошибочного бита (одиночной ошибки) ни одно из этих четырех кодовых слов 001, 010, 100, 111 не меняется на одно из трех других действительных кодовых слов. Получатель распознает, когда z. Б. Приходит 011, что, должно быть, произошла ошибка. Код с расстоянием Хэмминга 2 не может быть исправлен надежно, как показывает этот пример: 011 мог быть создан путем реверсирования всего одного бита одного из трех допустимых кодовых слов 001, 010, 111.

Если получатель предполагает, что возникают только единичные ошибки, и получатель хочет их исправить, он должен согласиться с кодовыми словами отправителя, каждое из которых имеет расстояние Хэмминга ≥ 3, например Например, 01011, 01100, 10010, 10101.

Двойная ошибка открывает возможность ошибки, как может быть показано в примере 01111: если 01111 должен был возникнуть из-за двойной ошибки из 01100, но получатель считает это одиночной ошибкой и исправляет ее, тогда 01100, фактически предназначенный отправителем, становится 01100 из-за двойной ошибки 01111 и неправильно 01011 из-за исправления получателя (из-за допущения единственной ошибки).

Из-за уже упомянутого уменьшения вероятности множественных ошибок (n-кратных ошибок) с увеличением n для большинства приложений достаточно расстояния Хэмминга от 4 (обнаружение тройных ошибок) до 5 (исправление двойных ошибок).

Требуемая длина кодового слова зависит от требуемого расстояния Хэмминга и количества возможных положений переключателя и показана в таблице выше. Здесь вы можете увидеть, например, что по крайней мере 8 битов должны быть переданы для 20 различных положений переключателя, если все 20 кодовых слов должны достичь по крайней мере расстояния Хэмминга ≥ 3 друг от друга.

Представление битовой строки в гиперкубе

пример

Если выбран код со словами <000, 101, 110, 011>, минимальное расстояние Хэмминга равно 2. При расстоянии Хэмминга 2 1-битные ошибки могут быть только распознаны, но не исправлены (например, признать, что 111 представляет собой неправильное слово, но не следует ли его исправлять после 110, 011 или 101).

Минимальное расстояние

пример

Вывод

Источник

Расстояние Хэмминга

Установление степени сходства между текстами – задача, которая часто встречается в повседневной работе. В частности данный подход может пригодится при нечетком поиске, при работе с данными с возможными погрешностями(например, если данные «восстанавливаются» их распознанного документа или), а также при работе с персональными данными, качество которых, зачастую, зависит от человеческого фактора. Ранее мы уже рассматривали один из наиболее эффективных алгоритмов для сравнения двух последовательностей символов, применительно к возможным опечаткам в ФИО (расстояние Левенштейна — ссылка, схожество Джаро — Винклера — ссылка). Сегодня поговорим о другом способе вычисления редакционного расстояния и о кейсах, в которых он может быть наиболее применимым.

Один из самых простых подходов к вычислению дистанции между строками. Это число позиций, в которых соответствующие символы двух слов одинаковой длины различны. Изначально использовалось для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей. Еще раз обратим внимание, что данный алгоритм применим только для строк одинаковой длины, при вычислении расстояния строки посимвольно сравниваются, и число «несовпадающих» символов и будет нашим результатом.

На языке программирования C# реализация будет выглядеть так:

Или с использование LINQ вот так:

Где можно применить данный алгоритм? Учитывая, что происходит банальное посимвольное сравнение, без учета операций перестановки, удаления, вставки символов, причем со строками одинаковой длины, данный алгоритм может пригодиться разве что при сравнении некоторых «условно-числовых» значений, которые могут встретиться среди персональных данных(например серия и номер паспорта, ИНН, номер счета, СНИЛС, номер водительского удостоверения), но даже при таком искусственном ограничении — не всегда. Рассмотрим пару кейсов:

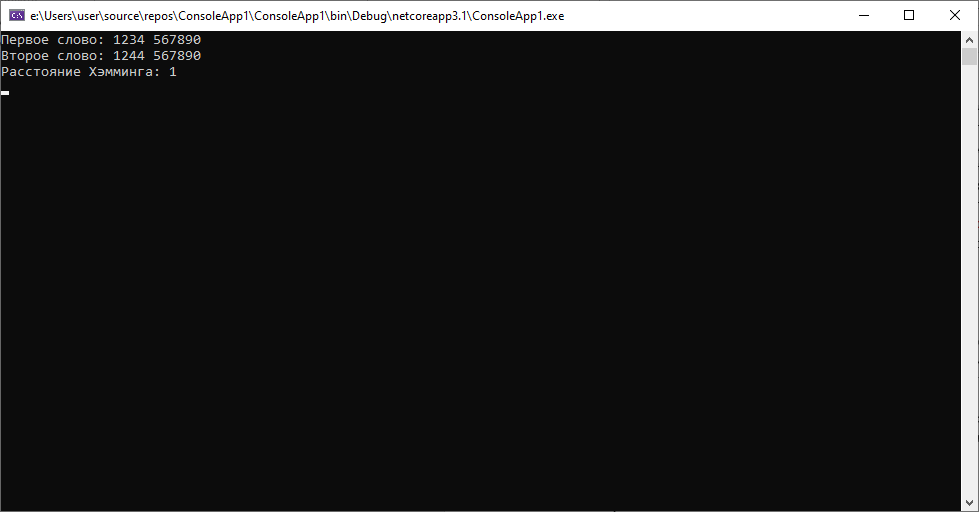
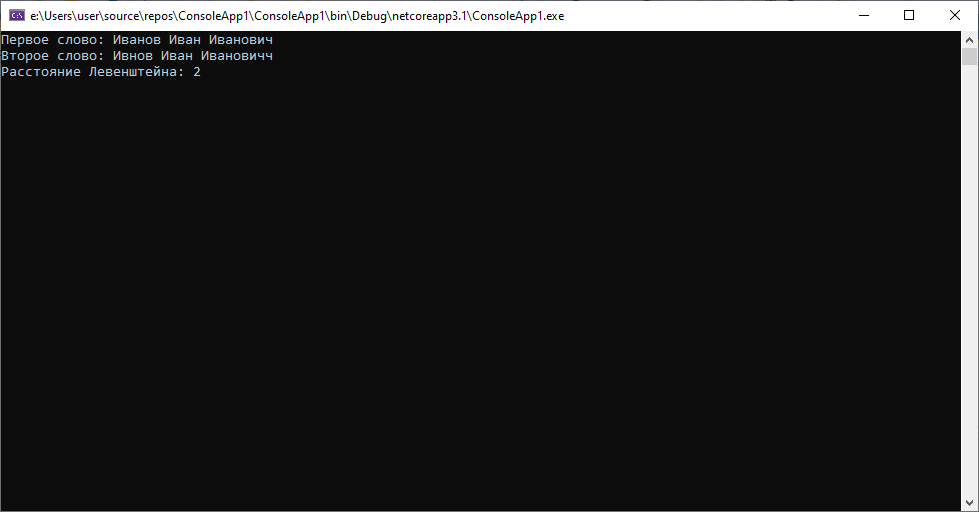
1.Паспортные данные клиентов 1234 567890 и 1244 567890, полученные из разных источников(допустим одни данные из автоматизированной системы, а вторые — распознанные данные со скана договора) для клиента Иванова Ивана Ивановича 01.01.1990. Для такой ситуации расстояние будет следующим:

Как мы видим дистанция между строками небольшая, как и предполагалось, ведь они отличаются всего на один символ.

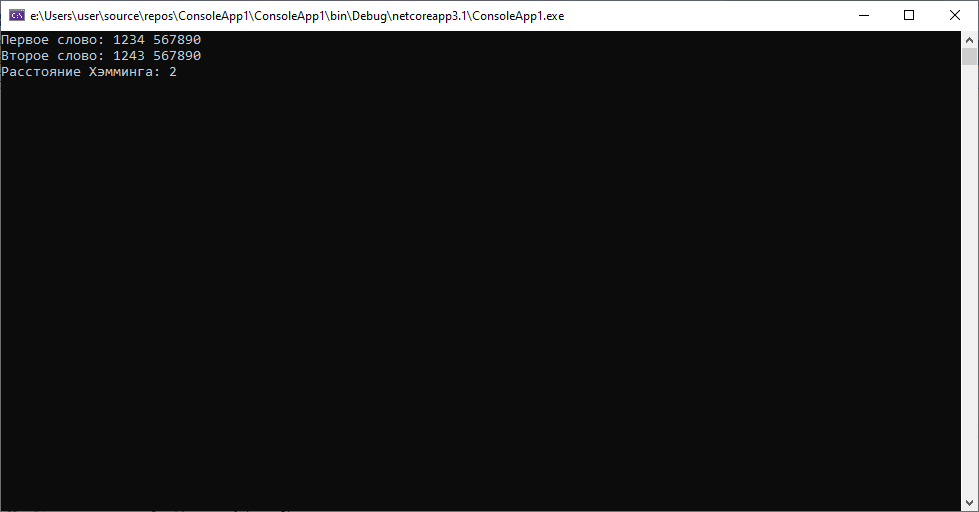
2.Предположим, что теперь наши данные таковы: 1234 567890 и 1243 567890(допустим, оба документа «пришли» к нам из разных автоматизированных систем). В данном случае алгоритм Хэмминга покажет следующее:

Здесь мы видим, что при минимальном различии(для нас очевидно, что в одном из случаев была «опечатка» — сотрудник неверно последовательно ввел 2 символа), расстояние уже будет равно 2. В то время, как при вычислении расстояния Левенштейна результат будет равен 1. Вывод: использование данного алгоритма для сравнения строк одинаковой длины возможно(и иногда уместно, учитывая простоту вычислений), но требует большего внимания при работе с данными, иногда расстояние может быть достаточно велико в случаях пропуска символов.

При этом расстояние Левенштейна во втором случае будет таковым.

Выводы: В случае работы с ФИО лучше использовать расстояние Левенштейна, не говоря уже о том, что строки могут быть по разным причинам не одинаковой длины. Однако в случае обработки значений заведомо фиксированной длины с небольшим количеством опечаток, расстояние Хэмминга может быть неплохим выбором для решения задачи.

Источник

Расстояние Хэмминга

Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга между двумя двоичными последовательностями (векторами) и длины называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures ). Расстояние Хэмминга является частным случаем метрики Минковского:

.

Примеры

Свойства

Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:

Расстояние Хэмминга в биоинформатике и геномике

Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.

При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.

См. также

Примечания

Литература

Полезное

Смотреть что такое «Расстояние Хэмминга» в других словарях:

расстояние Хэмминга — Число позиций, в которых два слова одинаковой длины отличаются друг от друга. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория передачи… … Справочник технического переводчика

Расстояние Хемминга — Расстояние Хэмминга мера (точнее, метрика) различия объектов одинаковой размерности. Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными … Википедия

Расстояние Левенштейна — (также редакционное расстояние или дистанция редактирования) между двумя строками в теории информации и компьютерной лингвистике это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на… … Википедия

Расстояние кода — в теории кодирования метрики отличий кодов. Наиболее используемыми расстояниями являются: Расстояние Хэмминга Расстояние Левенштейна Расстояние Йенцена Шаннона См. также Объём кода Граница кода … Википедия

Код Хэмминга — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия

Медаль Ричарда Хэмминга — (англ. Richard W. Hamming Medal) награда, присуждаемая ежегодно институтом инженеров электротехники и электроники (англ. IEEE) за исключительный вклад в науку об информации, информационные системы и технологии. К награде могут… … Википедия

Хэмминг, Ричард Уэсли — Ричард Уэсли Хэмминг Richard Wesley Hamming Дата рождения: 11 февраля 1915(1915 02 11) Место рождения: Чикаго, Иллинойс Дата смерти … Википедия

Неравенство Гильберта-Варшамова — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе неравенство Варшамова … … Википедия

Неравенство Гильберта — Варшамова — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе … … Википедия

Неравенство Варшамова-Гильберта — Неравенство Гильберта Варшамова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта Шеннона Варшамова, а в русскоязычной научной литературе неравенство Варшамова … … Википедия

Источник

Код Хэмминга (7; 4)

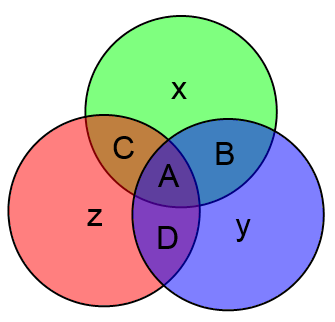
Структурно слова кода Хэмминга состоят из двух частей. Сначала идут информационные 4 бита, затем три бита проверочных. Будем обозначать информационные биты буквами ABCD, проверочные буквами xyz.

Таким образом слово кода Хэмминга имеет следующую структуру:

Для передачи 4 бит информации нам требуется передавать кодовое слово из целых 7 бит! Последние три бита в случае, когда ошибки отсутствуют, не несут никакой новой информации, ибо они зависят от первых 4. Однако если в кодовом слове из 7 бит произошла 1 ошибка, то исходные информационные 4 бита всё равно можно будет восстановить точно! В этом и состоит главная особенность самокорректирующихся кодов.

Для подсчёта проверочных бит можно использовать следующие формулы:

где n mod 2 означает остаток от деления числа n на 2.

К примеру, если информационный вектор есть ABCD = 1001, то кодовый вектор будет ABCDxyz = 1001 100

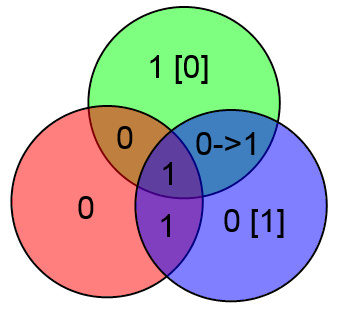
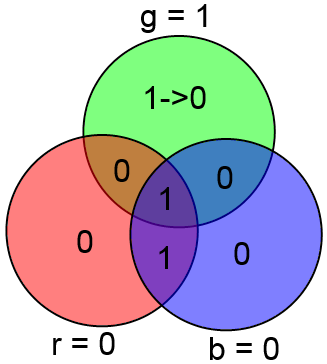
Вместо непонятных формул можно использовать следующую картинку:

Здесь всё очень просто. Подставляете вместо букв значения соответствующих битов и затем считаете значения x, y и z как сумму по модулю 2 тех информационных бит, которые есть в соответствующем круге.

В приведённом выше примере будет:

Куда более интересным является вопрос об исправлении ошибок. Очевидно, вывод об отсутствии ошибок приёмник может сделать просто взяв информационные биты ABCD, посчитав на их основе проверочные биты xyz и сравнить посчитанные проверочные биты с принятыми. Если есть ошибка, то часть проверочных битов не совпадёт.

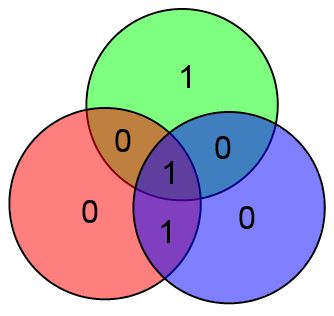
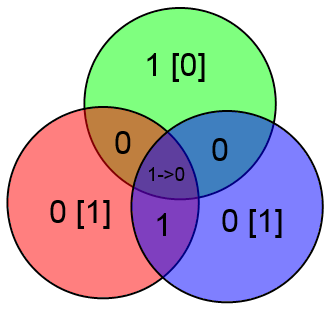
Предположим что произошла ошибка в проверочном бите y и было принято слово 1001 110

В таком случае два проверочных бита сойдутся, а один нет. Этого вполне достаточно чтобы сделать вывод что нужно исправить бит y (для которого проверка не сошлась).

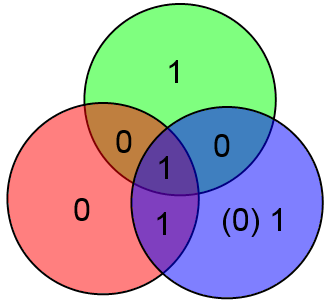
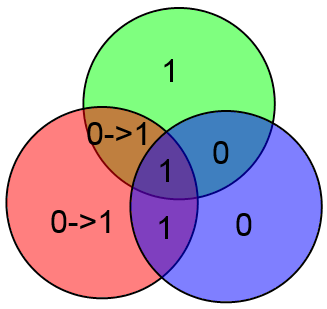
Наконец, отдельно рассмотрим бит A. Если в нём ошибка, то у нас не сойдутся все три проверки:

Увидев такое безобразие сразу же делаем вывод о том, что ошибка в бите A.

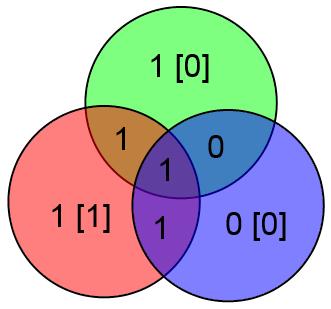
Таким образом, можно легко и просто вычислять локацию ошибки и исправлять её. Замечу что если ошибок больше одной, то описанный выше алгоритм сработает неверно. К примеру, допустим что произошли ошибки в битах C и z:

Проверочные биты y и z сойдутся, а бит x нет. Алгоритм исправит бит x и всё. Это вполне естественное поведение, т.к. если вероятность ошибки p 0).

Естественно, работать с цветными кругами удобно человеку, но неудобно компьютеру. У кодов Хэмминга есть одна особенность, которая позволяет их лёгкое декодирование на компьютере. Итак, рассмотрим следующий алгоритм:

Определим числа g, b, r как сумму всех четырёх бит в кругах соответствующего цвета. Т.е.:

g = A + B + C + x mod 2,

b = A + B + D + y mod 2,

r = A + C + D + z mod 2.

Фактически каждый из этих бит можно определить как сумму соответствующего проверочного бита, вычисленного на основании принятых информационных бит, с принятым проверочным битом. Т.е. к примеру g есть сумма (A + B + C mod 2) (по этой формуле считался x на стороне передатчика) и принятого x. Аналогично b соответствует y, r соответствует z.

Если ошибок нет, то gbr = 000 (принятые проверочные биты сошлись с вычисленными на основе информационного вектора).

Если же есть 1 ошибка, то число gbr есть номер (в двоичной записи) ошибочного бита в векторе ABCxDyz.

В качестве примера рассмотрим уже знакомый нам вектор ABCDxyz = 1001 100, в котором произошла ошибка в бите x (четвёртый бит в векторе ABCxDyz). Посчитаем gbr:

gbr = 100 [2] = 4 [10]. Ошибка в 4 бите, которым и является x. Таким образом, для декодирования и исправления ошибки в кодовом слове длины 7 требуется лишь вычислить три суммы и из полученного числа несложной функцией получить местонахождение ошибки.

Источник