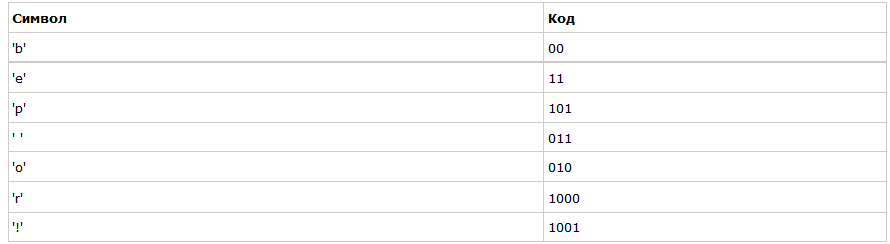
неравномерный двоичный код это
Равномерные и неравномерные двоичные коды. Условие Фано
Кодирование символов обычно предполагает, что каждому символу всегда сопоставляется одинаковое количество битов (например, в кодовой таблице ASCII каждому символу сопоставляется один байт, хранящий порядковый номер того или иного символа в этой таблице). Такой способ кодирования прост и удобен, однако очевидно, что он является не самым оптимальным. Для значительной части символов используются не все биты отведенных под них байтов (часть старших битов — нулевые), а при наличии в тексте только части символов, предусмотренных в таблице ASCII (например, если текст содержит только прописные русские буквы), приходится все равно использовать 8-битный код.
Более компактным является неравномерный двоичный код (особенно если при его построении исходить из частоты встречаемости различных символов и присваивать наиболее часто используемым знакам самые короткие коды, как это сделано в методе Хаффмана). При этом количество битов, отводимых для кодирования символов, в целом зависит от количества используемых в конкретном случае различных символов (от мощности алфавита), а коды, соответствующие разным символам, могут иметь различную длину в битах.
Главное при таком кодировании — обеспечить возможность однозначного декодирования записанной с помощью этих кодов строки (поочередного, слева направо, выделения и распознавания из сплошной последовательности нулей и единиц кодов отдельных букв). Для этого коды символам необходимо назначать в соответствии с условиями Фано.
Прямое условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого, более длинного кода.
Обратное условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с окончанием (постфиксом) какого-либо другого, более длинного кода.
Для однозначности декодирования последовательности кодов достаточно выполнения хотя бы одного из двух вышеуказанных условий Фано:
— при выполнении прямого условия Фано последовательность кодов однозначно декодируется с начала;
— при выполнении обратного условия Фано последовательность кодов однозначно декодируется с конца.
Выбрать, какое из двух правил Фано используется при решении конкретной задачи, можно, проанализировав коды в условии задачи (без учёта кода, проверяемого в вариантах ответа): если для исходных кодов выполняется прямое правило Фано, то его и нужно использовать при решении, и наоборот.
Вместе с тем нужно помнить, что правила Фано — это достаточное, но не необходимое условие однозначного декодирования: если не выполняется ни прямое, ни обратное правило Фано, конкретная двоичная последовательность может оказаться такой, что она декодируется однозначно (так как остальные возможные варианты до конца декодирования довести не удаётся). В подобном случае необходимо пытаться строить дерево декодирования в обоих направлениях.
Рекомендуется начинать решение задач такого типа с анализа выполнимости правил Фано для исходных кодов, указанных в условии задачи (т.е. без учета искомого кода в вариантах ответов). В зависимости от того, какое из двух правил Фано выполняется для исходных кодов, при дальнейшем решении задачи производится сравнение более короткого кода с началом (при выполнении прямого правила Фано) или с концом (при выполнении обратного правила Фано) более длинного кода.
Если для заданной последовательности кодов выполняется прямое правило Фано, то её декодирование необходимо вести с начала (слева направо).
Если для заданной последовательности кодов выполняется обратное правило Фано, то её декодирование необходимо вести с конца (справа налево).
При сравнении пары кодов удобно подписывать более короткий код под более длинным, выравнивая эти записи по левому краю — для прямого правила Фано либо по правому краю — для обратного правила Фано.
Разбор типовых задач
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А-1, Б-000, В-001, Г-011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.
Равномерные и неравномерные коды.
Дата добавления: 2015-08-14 ; просмотров: 32643 ; Нарушение авторских прав
Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Соответственно, кодирование называется равномерным, если соответствующий ему код имеет постоянную длину. В настоящее время в информатике более употребительно равномерное кодирование, оно проще и более удобно. В компьютерах при кодировании информации в основном используются равномерные коды, соответствующие размерам компьютерных ячеек.
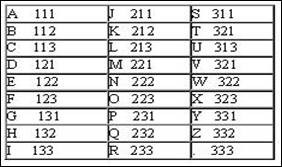
Другим интересным примером равномерного кода является код Трисиме, в котором знакам латинского алфавита ставятся в соответствие кодовые слова длины 3 над алфавитом из 3-х символов: <1, 2, 3>. Этот код представлен в следующей таблице :
Понятно, что код Трисиме не может кодировать более чем 3 3 =27 символов.
Число букв в алфавите кода называется основанием кода, а длина кодовых слов равномерного кода называется порядком кода. Коды с основанием 2, как уже говорилось, называются двоичными, а с основанием 3 – троичными, и так далее. Так код Бодо имеет основание 2, а порядок 5, а у кода Трисиме и основание, и порядок равны 3.
Код называется неравномерным (или кодом переменной длины), если его кодовые слова имеют разное число букв (неодинаковую длину слов). Соответственно, кодирование называется неравномерным, если соответствующий ему код неравномерный.
Типичным примером неравномерного кода является телеграфный код, который принято называть азбукой Морзе. На следующей таблице представлен код азбуки Морзе для русского алфавита:
| A | • − | И | • • | P | • − • | Ш | − − − − | • − − − − | − − − − • | |
| Б | − • • • | Й | • − − − | С | • • • | Щ | − − • − | • • − − − | − − − − − | |
| В | • − − | К | − • − | Т | − | Ъ | • − − • − • | • • • − − | Точка | • • • • • • |
| Г | − − • | Л | • − • • | У | • • − | Ь | − • • − | • • • • − | Запятая | • − • − • − |
| Д | − • • | М | − − | Ф | • • − • | Ы | − • − − | • • • • • | / | − • • − • |
| Е | • | H | − • | Х | • • • • | Э | • • − • • | − • • • • | ? | • • − − • • |
| Ж | • • • − | О | − − − | Ц | − • − • | Ю | • • − − | − − • • • | ! | − − • • − − |
| З | − − • • | П | • − − • | Ч | − − − • | Я | • − • − | − − − • • | @ | • − − • − • |
Американский изобретатель телеграфа Сэмюель Морзе разработал этот код в 1838 году для передачи телеграфных сообщений в виде последовательности электрических сигналов, передаваемых от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Этот код был придуман Морзе задолго до научных исследований
 |
| СэмюэлМорзе (1791-1872) |
относительной частоты появления различных букв в текстах, но, тем не менее, Морзе при составлении кода использовал принцип частоты букв. Буквам, используемым чаще, им присвоены короткие кодовые комбинации, редко используемым буквам – длинные. Морзе оценил относительную частоту букв английского языка подсчетом литер в ячейках типографской наборной машины. Наиболее часто используемой букве «Е» (в английском языке) он присвоил наиболее короткий код «точка». Следующей по количеству литер букве он присвоил код несколько большей длительности и так далее.
При составлении азбуки Морзе для букв русского алфавита учет относительной частоты букв не производился, и это повысило его избыточность. Расчеты избыточности кода Морзе на основании проведенных исследований частоты появления букв показали, что для букв английского алфавита она составляет 19%, для букв русского алфавита 22%.
Преимущество у неравномерных кодов перед равномерными как раз и состоит в том, что сообщения можно передавать более экономным способом, так как часто передаваемые кодовые слова более короткие, а значит, кодовая последовательность может иметь меньшую длину, чем для равномерных кодов. Ниже это будет показано.
Но у неравномерных кодов есть серьезный недостаток по сравнению с равномерными кодами. У равномерных кодов кодовая последовательность всегда декодируется однозначно за счет того, что кодовые слова имеют одинаковую длину (кодовая последовательность легко делится на кодовые слова). Но не для всех неравномерных кодов достигается однозначность декодирования кодовых последовательностей. Мы уже видели это, пытаясь рассматривать азбуку Морзе как двоичный код.
Этот код неравномерный (кодовые слова разной длины).
Закодируем последовательность сообщений: s7s7. Имеем F(s7s7)=B=111111. Но эта последовательность может быть декодирована и по-другому, так как: B=F(s3s3s3)= F(s1s3s7)=F(s3s7s1)=F(s1s1s1s1s1s1s1s). Как видим, способов декодирования много (подсчитайте: сколько их?). Неоднозначно декодируется и следующая последовательность:
11011011 (а сколько здесь способов декодирования?). Очевидно, что такой код практически использовать нельзя. А если мы изменим код так, чтобы он стал равномерным, например, доопределим функцию F так:
то теперь никаких проблем с декодированием не будет.
MT1402: Теоретические основы информатики. Имитационное моделирование
Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды
Как следует из названия, в способах кодировании, относящихся к этой группе, знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы %%(τ_0 = τ_1 = τ)%%. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время %%K(A,2) \cdot τ%%.
Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность элементарных сигналов:
Неравномерный код с разделителем
В соответствии с перечисленными правилами построим кодовую табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 2.1.) вероятностях появления отдельных букв.
Теперь можно найти среднюю длину кода К(r,2) для данного способа кодирования:
Поскольку для русского языка, %%I_1(r) = 4,356 бит%%, избыточность данного кода, согласно (3.5), составляет:
это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение %%К(e,2) = 4,716%%, что при %%I_1(e) = 4,036%% бит приводят к избыточности кода %%Q(e,2) = 0,168%%.
| Буква | Код | %%p_j\cdot 10^3%% | %%k_j%% | Буква | Код | %%p_j\cdot 10^3%% | %%k_j%% |
|---|---|---|---|---|---|---|---|
| пробел | 000 | 174 | 3 | я | 1011000 | 18 | 7 |
| о | 100 | 90 | 3 | ы | 1011100 | 16 | 7 |
| е | 1000 | 72 | 4 | з | 1101000 | 16 | 7 |
| а | 1100 | 62 | 4 | ь,ъ | 1101100 | 14 | 7 |
| и | 10000 | 62 | 5 | б | 1110000 | 14 | 7 |
| т | 10100 | 53 | 5 | г | 1110100 | 13 | 7 |
| н | 11000 | 53 | 5 | ч | 1111000 | 12 | 7 |
| с | 11100 | 45 | 5 | й | 1111100 | 10 | 7 |
| р | 101000 | 40 | 6 | х | 10101000 | 9 | 8 |
| в | 101100 | 38 | 6 | ж | 10101100 | 7 | 8 |
| л | 110000 | 35 | 6 | ю | 10110000 | 6 | 8 |
| к | 110100 | 28 | 6 | ш | 10110100 | 6 | 8 |
| м | 111000 | 26 | 6 | ц | 10111000 | 4 | 8 |
| д | 111100 | 25 | 6 | щ | 10111100 | 3 | 8 |
| п | 1010000 | 23 | 7 | э | 11010000 | 3 | 8 |
| у | 1010100 | 21 | 7 | ф | 11010100 | 2 | 8 |
Рассмотрев один из вариантов двоичного неравномерного кодирования, попробуем найти ответы на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?
Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом*) какого-либо иного более длинного кода.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Пример.Пусть имеется следующая таблица префиксных кодов:
| а | л | м | р | у | ы |
|---|---|---|---|---|---|
| 10 | 010 | 00 | 11 | 0110 | 0111 |
Требуется декодировать сообщение:
Декодирование производится циклическим повторением следующих действий:
Применение данного алгоритма дает:
| шаг | рабочее слово | текущее сообщение | распознанный знак | декодированное сообщение |
|---|---|---|---|---|
| 0 | Пусто | 0010001000011101010101110000110 | — | — |
| 1 | 0 | 0100010000111010101110000110 | нет | — |
| 2 | 00 | 1000100001110101011110000110 | м | м |
| 3 | 1 | 0001000011101010101110000110 | нет | м |
| 4 | 10 | 0010000111010101110000110 | а | ма |
| 5 | 0 | 010000111010101110000110 | нет | ма |
| 6 | 00 | 10000111010101110000110 | м | мам |
| . |
Доведя процедуру до конца, получим сообщение: «мама мыла раму».
Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.
wiki.vspu.ru
портал образовательных ресурсов
Алфавитное неравномерное двоичное кодирование. Префиксный код. Код Хаффмана
Алфавитное неравномерное двоичное кодирование— кодирование при котором символы некоторого первичного алфавита кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться.
Префиксный код в теории кодирования— код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.
Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.
0 10 0 11 0 11 10
0 100 11 0 11 10
Префиксные коды широко используются в различных областях информационных технологий. На них основаны многие алгоритмы сжатия информации. Их используют различные протоколы. К префиксным кодам относятся такие распространённые вещи, как:
• Юникод,
• телефонные номера,
• Код Хаффмана,
• Код Фибоначчи и мн. другие.
Код Хаффмана
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). В данной статье я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Я мог бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
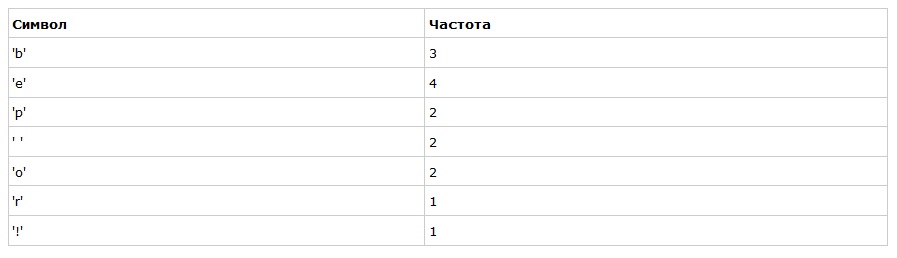
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит.
Чтобы получить код для каждого символа строки «beep boop beer!»,на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
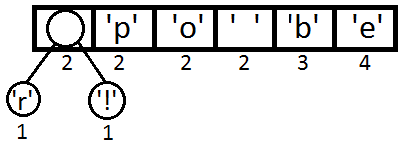
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
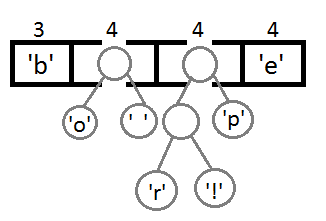
Повторим те же шаги и получим последовательно:
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для „b“, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на „b“.
Универсальное двоичное кодирование. Равномерные и неравномерные коды.
Урок 9. Информатика 7 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Универсальное двоичное кодирование. Равномерные и неравномерные коды.»
На прошлом уроке мы узнали:
· Для удобства хранения и передачи информации её часто переводят из непрерывной формы в дискретную. Такой процесс называется дискретизацией.
· В процессе дискретизации информация записывается на одном из языков.
· Алфавитом языка называются все существующие символы, которые используются для представления информации на этом языке.
· Алфавит характеризуется своей мощностью, это количество символов, которые в него входят.
· Двоичный алфавит состоит из двух символов. Запись информации с помощью такого алфавита называется двоичным кодированием.
· Двоичный код – это код информации, получившийся в результате её двоичного кодирования.
· Любой алфавит можно привести к двоичному.
· Двоичное кодирование звука.
· Двоичное кодирование изображения.
· Равномерный и неравномерный коды.
· Двоичное кодирование текстовых сообщений методом Хаффмана.
Итак, на прошлом уроке мы узнали, что любой алфавит можно представить в виде двоичного, для этого каждому символу исходного алфавита присваивается его двоичный код. Записывая подряд двоичные коды всех символов, мы можем кодировать текстовые сообщения. Ещё мы узнали, что двоичный алфавит легко реализовать технически, с помощью наличия или отсутствия электрического сигнала на некотором участке электрической цепи. Именно поэтому любая информация на компьютере представлена в виде двоичного кода. Однако мы знаем, что на компьютере может храниться любая информация, а не только текстовая или числовая. Как же её представить в виде двоичного кода? Например звук и изображение. Как мы знаем, они представляются в виде непрерывных сигналов, разберёмся как же представить эти два вида информации в дискретной форме.
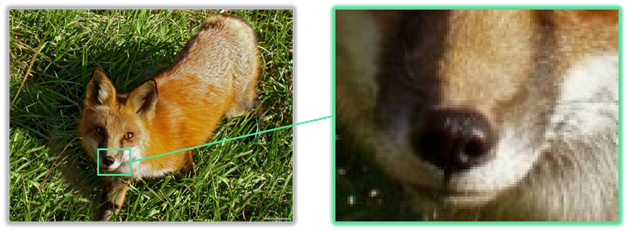
Начнём с изображения. Вполне логично, что любое изображение можно разделить на некоторые участки, каждый из которых имеет свой цвет. Именно так происходит при представлении изображений на компьютере. Изображение разбивается на маленькие фрагменты, которые можно назвать точками. Каждое изображение имеет своё разрешение. Оно состоит из двух цифр, которые разделяются крестиком или двоеточием. Число слева, означает, на сколько точек делится изображение по горизонтали, а справа – на сколько по вертикали. Таким образом изображение на компьютере представляется в виде последовательности точек, каждая из которых имеет свой цвет. То есть изображение на компьютере можно представить, последовательно записав цвета всех точек, которые в него входят.
Но как же представить цвет в виде двоичных кодов? Любой цвет на мониторе компьютера изображается смешиванием в разных количествах трёх основных цветов: красного, зелёного и синего. Такое представление цветов называется их RGB-моделью. По первым буквам названий основных цветов на английском языке, то есть «Rad», «Green» и «Blue». Так, как остальные цвета – это смеси трёх основных цветов в разных количествах, их можно представить в виде трёх чисел, количеств основных цветов. Эти числа можно заменить двоичными кодами одинаковой разрядности. Записав эти коды последовательно, мы получим двоичный код цвета точки. Таким образом изображение на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает цвет одной из точек изображения.
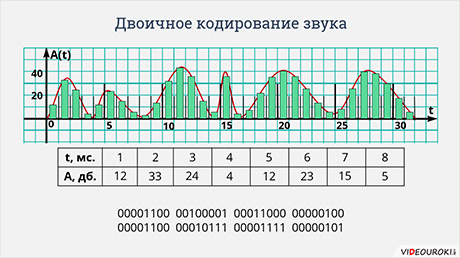
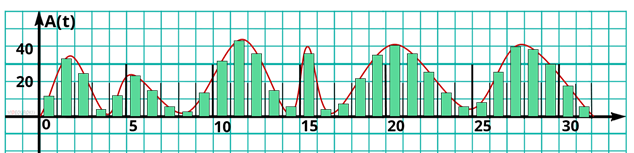
Немного иначе происходит двоичное кодирование звука. Позже из курса физики вы узнаете, что любой звук можно представить в виде непрерывной волны. Эту волну можно описать, зависимостью её амплитуды, то есть громкости звука от времени. Такую зависимость легко изобразить в виде графика. Чтобы представить звук в виде дискретных сигналов, время, в течение которого продолжается звук, делится на равные небольшие промежутки. И на каждом из промежутков заново определяется амплитуда волны, то есть громкость звука.
То, есть звук можно представить в виде списка чисел, каждое из которых означает амплитуду волны, в течение небольшого промежутка времени. Эти числа можно представить в виде двоичных кодов с одинаковым количеством разрядов. Таким образом звук на компьютере представляется в виде списка двоичных кодов одинаковой разрядности, каждый из которых обозначает амплитуду звуковой волны на некотором небольшом промежутке времени.
Мы знаем, что с помощью двоичного кодирования в виде последовательности единиц и нулей можно представить любую информацию на естественном или формальном языке, в том числе изображение и звук. То есть информацию из любой формы можно представить в виде двоичного кода, что означает универсальность двоичного кодирования. Это и есть его главное преимущество. Главный недостаток двоичного кодирования – это большой размер двоичного кода. Так при кодировании текстового сообщения одному символу текста может соответствовать несколько символов двоичного кода.
Давайте подумаем, как можно уменьшить размер двоичного кода, и вообще любого кода. До этого все двоичные коды, которые мы рассматривали, были равномерными. Равномерным называется код, который состоит из равных по количеству разрядов кодовых комбинаций. Так например при кодировании алфавита для каждой буквы мы использовали двоичные коды с одинаковым количеством разрядов. Однако не все символы алфавита в текстовом сообщении, встречаются одинаково часто. Поэтому, для того, чтобы сократить длину двоичного кода мы можем присвоить разным сигналам коды разной длины. Коды с меньшей разрядностью можно присвоить сигналам, которые в сообщении встречаются чаще, а коды с большей разрядностью – сигналам, которые встречаются в сообщении реже. Такой код называется неравномерным, то есть он состоит из комбинаций различной длины.
Пример неравномерного кода – азбука Морзе. В ней разным буквам алфавита, соответствует разное количество сигналов, длинных и коротких. Например буква «А» обозначается всего двумя сигналами: одним коротким и одним длинным. А твёрдый знак кодируется пятью сигналами: двумя длинными, одним коротким и двумя длинными.
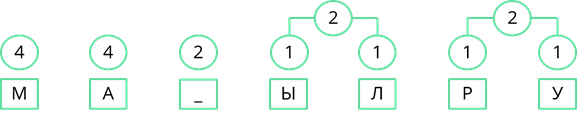
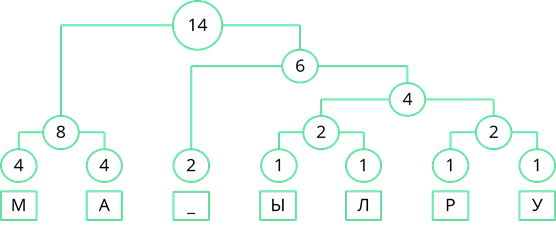
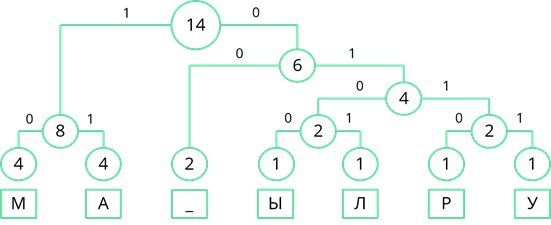
Рассмотрим один из методов неравномерного кодирования текстовых сообщений. Он называется методом Хаффмана. Посмотрим, как работает этот метод, закодировав с его помощью сообщение: «МАМА МЫЛА РАМУ». Сначала выпишем все символы алфавита, который используется в сообщении. В данном сообщении используются символы: «М», «А», пробел, «Ы», «Л», «Р» и «У». Затем нужно записать, как часто в сообщении встречается каждый из символов. Буквы «М» и «А» повторяются по четыре раза. Пробел повторяется дважды. Буквы «Ы», «Л», «Р» и «У» в сообщении встречаются по одному разу. Затем символы сообщения записываются в порядке убывания частоты появления. У нас они так и записаны.
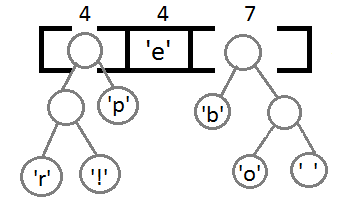
Теперь строится дерево частоты появления символов в сообщении. В начале берутся два символа, которые встречаются в сообщении реже всех. У нас таких символа четыре, возьмём два правых, буквы «Р» и «У», соединяем их линией, и складываем их частоту появления в сообщении. 1 + 1 = 2.
Теперь повторим то же действие. Реже всех у нас появлялись буквы «Ы» и «Л». Соединим их линиями сложив частоту появления получим 2.
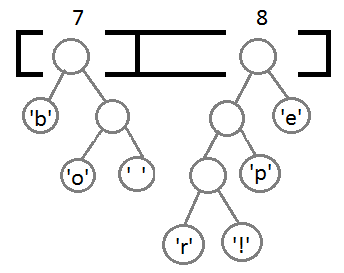
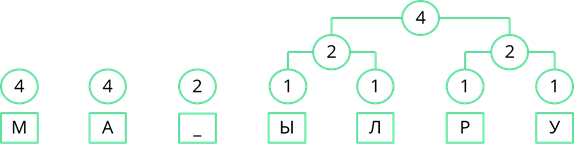
Теперь снова смотрим где у нас самая маленькая частота появления. Таких частот у нас три. Пробел появлялся дважды, двум равны и общие частоты появления символов «Ы» и «Л», и символов «Р» и «У». Возьмём две правые частоты и объединим их. Их суммарная частота равна 4.
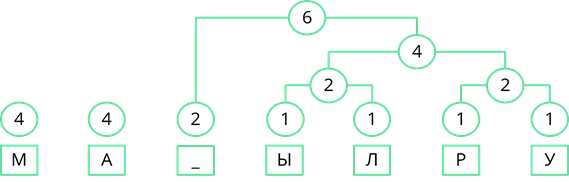
Снова ищем минимальные частоты появления. Возьмём две правые частоты и объединим их. Их сумма равна 6.
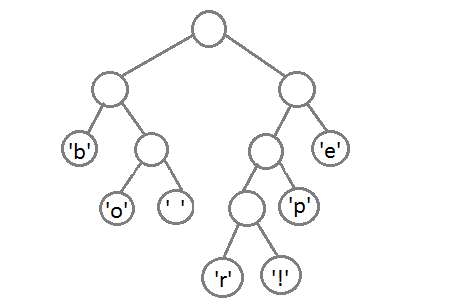
Теперь объединим две левые частоты. Их сумма равна 8.
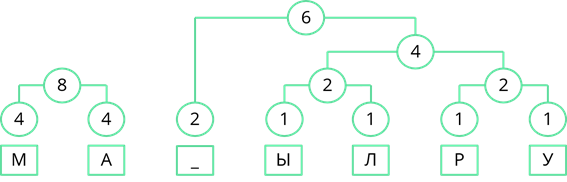
Объединим две оставшиеся частоты. Их сумма равна 14. Именно четырнадцати равна длина кодируемого сообщения.
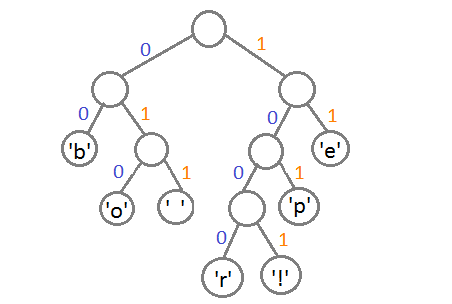
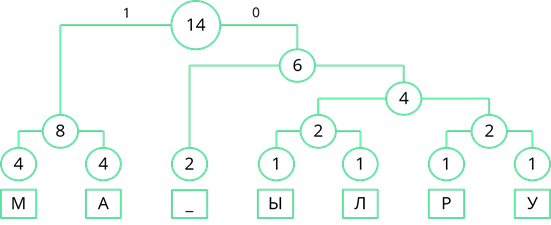
Теперь двигаясь, сверху вниз присвоим ветвям дерева значения 0 и 1. Ветви, с большей частотой будем присваивать 1, а ветви с меньшей частотой – 0. Так левой ветви верхнего узла присвоим 1, а правой – 0.
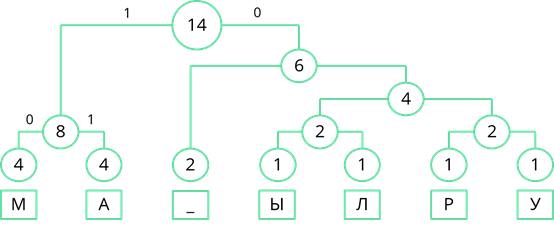
Затем рассмотрим левый узел. Там две частоты равны. Поэтому левой ветви присвоим 0, а правой – 1.
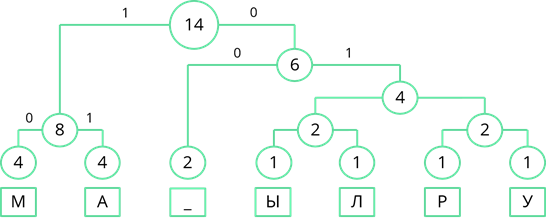
Рассмотрим узел, частота которого равна 6. Частота появления пробела меньше суммарной частоты правой ветви. Поэтому левой ветви присвоим 0, а правой ветви – 1.
По такому же принципу пронумеруем оставшиеся ветви дерева.
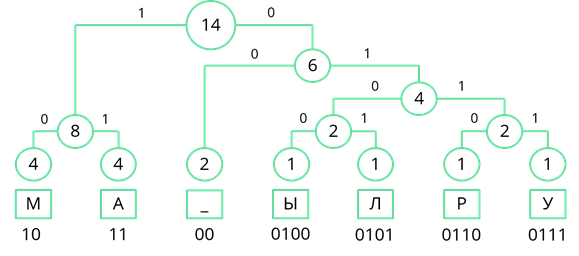
Теперь, двигаясь по получившемуся дереву сверху вниз, мы можем записать двоичный код каждого символа. Так у буквы «М» будет код 10, у буквы «А» – 11, у пробела – 00 и т. д…
Теперь нам остаётся лишь заменить все символы в сообщении их двоичными кодами. В итоге двоичный код нашего сообщения будет 101110110010010001011100011011100111. Всего в нём 36 разрядов.
У некоторых из вас может возникнуть вопрос, а как же расшифровать такое сообщение, ведь в отличии от равномерного кода мы не знаем точно сколько разрядов занимает каждый символ. При неравномерном кодировании достаточно, чтобы код никакого из символов не начинался с кода другого символа. Давайте попробуем расшифровать первые символы нашего сообщения.
Итак, сообщение начинается с единицы. С единицы у нас начинаются двоичные коды букв «М» и «А», посмотрев на следующий символ 0, мы можем точно определить, что первый символ – это буква «М». По такому же принципу мы можем определить, что, следующий символ буква «А» и до конца расшифровать слово «МАМА».
Следующая цифра – 0. С нуля у нас начинаются коды пяти символов. После него идёт так же 0. С 00 у нас начинается код пробела. Далее идёт буква «М». Следующая цифра – 0. С нуля у нас начинаются коды 5 символов. Возьмём следующую цифру. С 01 начинаются коды четырёх символов. Следующая цифра – 0. С 010 начинаются коды двух символов. Следующий символ – снова 0. И мы можем однозначно определить, что это буква «Ы». Так же расшифровывается и остальное сообщение.
Давайте посмотрим, двоичный код из скольких разрядов получился бы при использовании равномерного двоичного кодирования. Как мы помним сообщение записано с помощью алфавита мощностью 7 символов. Определим, разрядность двоичного кода, необходимую для кодирования одного символа такого алфавита. Как мы помним, для этого необходимо определить, в какую степень возвести цифру 2, чтобы получить 7. Но цифру семь мы так получить не можем, поэтому результат необходимо округлить в большую сторону. Мы можем так получить 8, для этого двойку нужно возвести в 3 степень. То есть для кодирования одного символа нам потребуется 3-разрядный двоичный код. Определим, какой код потребуется для кодирования всего сообщения, для этого нужно разрядность кода одного символа, то есть 3 умножить на длину всего сообщения, то есть 14. 3 × 14 = 42. То есть при кодировании сообщения нам потребовался бы 42-разрядный равномерный двоичный код. При использовании неравномерного кода нам потребовалось всего 36 разрядов, то есть на 6 разрядов меньше.
Сокращение длины двоичного кода заметно даже при небольшой длине сообщения. Если длина сообщения будет больше, например десятки тысяч символов, разница между длинами равномерного и неравномерного кода тоже увеличится. Когда длина двоичного кода составляет миллиарды разрядов – разница между равномерным и неравномерным кодом просто огромна.
· Универсальность двоичного кодирования означает, что его можно применять для кодирования информации на любом формальном или неформальном языке, а также изображений и звука.
· Все коды можно разделить на равномерные и неравномерные, где равномерный код состоит из комбинаций равной длины, а неравномерный код состоит из комбинаций разной длины.
· Использование неравномерного кодирования позволяет сократить длину кода.