неравномерный двоичный префиксный код
wiki.vspu.ru
портал образовательных ресурсов
Алфавитное неравномерное двоичное кодирование. Префиксный код. Код Хаффмана
Алфавитное неравномерное двоичное кодирование— кодирование при котором символы некоторого первичного алфавита кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться.
Префиксный код в теории кодирования— код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.
Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.
0 10 0 11 0 11 10
0 100 11 0 11 10
Префиксные коды широко используются в различных областях информационных технологий. На них основаны многие алгоритмы сжатия информации. Их используют различные протоколы. К префиксным кодам относятся такие распространённые вещи, как:
• Юникод,
• телефонные номера,
• Код Хаффмана,
• Код Фибоначчи и мн. другие.
Код Хаффмана
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). В данной статье я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Я мог бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит.
Чтобы получить код для каждого символа строки «beep boop beer!»,на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
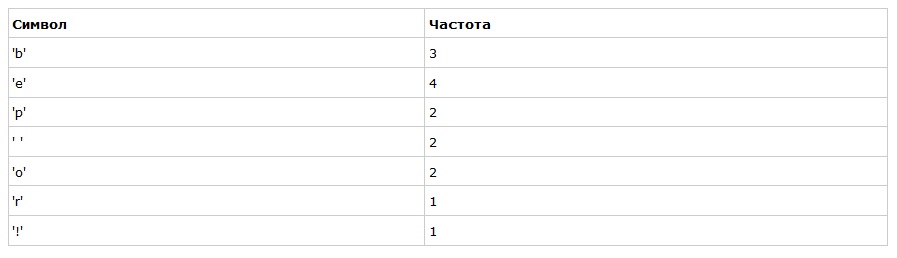
Для начала посчитаем частоты всех символов:
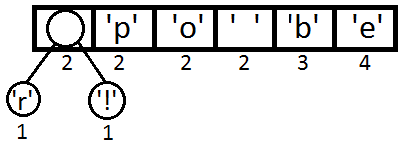
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
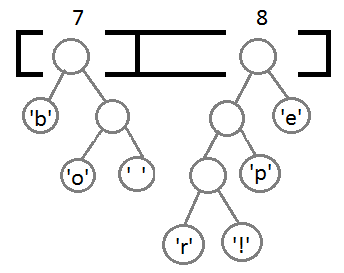
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.
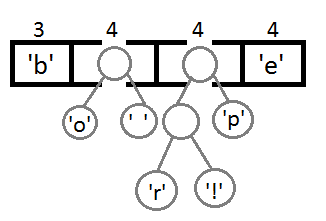
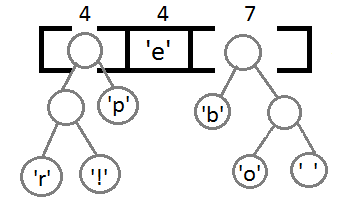
Повторим те же шаги и получим последовательно:
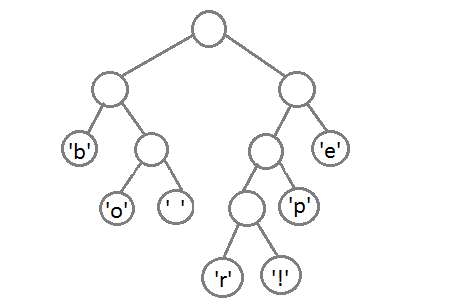
Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
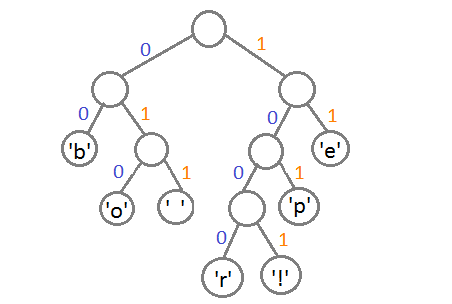
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
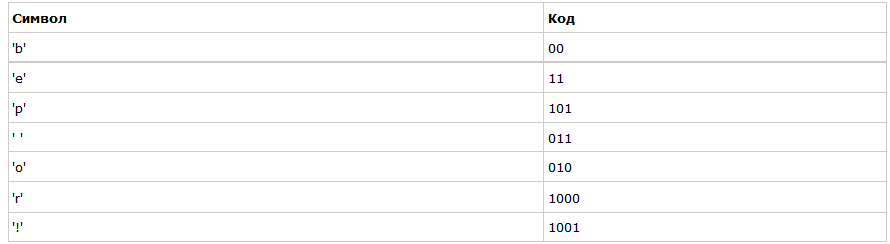
Если мы так сделаем, то получим следующие коды для символов:
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для „b“, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на „b“.
MT1402: Теоретические основы информатики. Имитационное моделирование
Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды
Как следует из названия, в способах кодировании, относящихся к этой группе, знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы %%(τ_0 = τ_1 = τ)%%. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время %%K(A,2) \cdot τ%%.
Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность элементарных сигналов:
Неравномерный код с разделителем
В соответствии с перечисленными правилами построим кодовую табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 2.1.) вероятностях появления отдельных букв.
Теперь можно найти среднюю длину кода К(r,2) для данного способа кодирования:
Поскольку для русского языка, %%I_1(r) = 4,356 бит%%, избыточность данного кода, согласно (3.5), составляет:
это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение %%К(e,2) = 4,716%%, что при %%I_1(e) = 4,036%% бит приводят к избыточности кода %%Q(e,2) = 0,168%%.
| Буква | Код | %%p_j\cdot 10^3%% | %%k_j%% | Буква | Код | %%p_j\cdot 10^3%% | %%k_j%% |
|---|---|---|---|---|---|---|---|
| пробел | 000 | 174 | 3 | я | 1011000 | 18 | 7 |
| о | 100 | 90 | 3 | ы | 1011100 | 16 | 7 |
| е | 1000 | 72 | 4 | з | 1101000 | 16 | 7 |
| а | 1100 | 62 | 4 | ь,ъ | 1101100 | 14 | 7 |
| и | 10000 | 62 | 5 | б | 1110000 | 14 | 7 |
| т | 10100 | 53 | 5 | г | 1110100 | 13 | 7 |
| н | 11000 | 53 | 5 | ч | 1111000 | 12 | 7 |
| с | 11100 | 45 | 5 | й | 1111100 | 10 | 7 |
| р | 101000 | 40 | 6 | х | 10101000 | 9 | 8 |
| в | 101100 | 38 | 6 | ж | 10101100 | 7 | 8 |
| л | 110000 | 35 | 6 | ю | 10110000 | 6 | 8 |
| к | 110100 | 28 | 6 | ш | 10110100 | 6 | 8 |
| м | 111000 | 26 | 6 | ц | 10111000 | 4 | 8 |
| д | 111100 | 25 | 6 | щ | 10111100 | 3 | 8 |
| п | 1010000 | 23 | 7 | э | 11010000 | 3 | 8 |
| у | 1010100 | 21 | 7 | ф | 11010100 | 2 | 8 |
Рассмотрев один из вариантов двоичного неравномерного кодирования, попробуем найти ответы на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?
Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом*) какого-либо иного более длинного кода.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Пример.Пусть имеется следующая таблица префиксных кодов:
| а | л | м | р | у | ы |
|---|---|---|---|---|---|
| 10 | 010 | 00 | 11 | 0110 | 0111 |
Требуется декодировать сообщение:
Декодирование производится циклическим повторением следующих действий:
Применение данного алгоритма дает:
| шаг | рабочее слово | текущее сообщение | распознанный знак | декодированное сообщение |
|---|---|---|---|---|
| 0 | Пусто | 0010001000011101010101110000110 | — | — |
| 1 | 0 | 0100010000111010101110000110 | нет | — |
| 2 | 00 | 1000100001110101011110000110 | м | м |
| 3 | 1 | 0001000011101010101110000110 | нет | м |
| 4 | 10 | 0010000111010101110000110 | а | ма |
| 5 | 0 | 010000111010101110000110 | нет | ма |
| 6 | 00 | 10000111010101110000110 | м | мам |
| . |
Доведя процедуру до конца, получим сообщение: «мама мыла раму».
Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.
Алфавитное неравномерное двоичное кодирование. Код Хаффмана
На этом шаге мы рассмотрим алфавитное неравномерное двоичное кодирование; префиксный код; код Хаффмана.
Равномерное кодирование удобно для декодирования. Однако часто применяют и неравномерные коды, т.е. коды с различной длиной кодовых слов. Это полезно, когда в исходном тексте разные буквы встречаются с разной частотой. Тогда часто встречающиеся символы стоит кодировать более короткими словами, а редкие – более длинными. Из примера 1 видно, что (в отличие от равномерных кодов!) не все неравномерные коды допускают однозначное декодирование.
Есть простое условие, при выполнении которого неравномерный код допускает однозначное декодирование.
Код из примера 1 – НЕ префиксный, так как, например, код буквы А (т.е. кодовое слово 1) – префикс кода буквы К (т.е. кодового слова 12, префикс выделен жирным шрифтом).
Код из примера 2 (и любой другой равномерный код) – префиксный: никакое слово не может быть началом слова той же длины.
Кодовые слова выписаны в алфавитном порядке. Видно, что ни одно из них не является началом другого. Это можно проиллюстрировать рисунком

Символы некоторого первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы ( 



Очевидно, возможны различные варианты двоичного кодирования, однако, не все они будут пригодны для практического использования – важно, чтобы закодированное сообщение могло быть однозначно декодировано, т.е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв. Проще всего этого достичь, если коды будут разграничены разделителем – некоторой постоянной комбинацией двоичных знаков. Условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов – 000 (признак конца слова – пробел). Довольно очевидными оказываются следующие правила построения кодов:
Длительность передачи каждого отдельного кода ti, очевидно, может быть найдена следующим образом: ti = ki • 
| Таблица 1. Таблица кодов | |||||||
| Буква | Код | pi·10 3 | ki | Буква | Код | pi·10 3 | ki |
| пробел | я | ||||||
| о | ы | ||||||
| е | з | ||||||
| а | ь,ъ | ||||||
| и | б | ||||||
| т | г | ||||||
| н | ч | ||||||
| с | й | ||||||
| р | х | ||||||
| в | ж | ||||||
| л | ю | ||||||
| к | ш | ||||||
| м | ц | ||||||
| д | щ | ||||||
| п | э | ||||||
| у | ф |
Теперь по формуле можно найти среднюю длину кода K (2) для данного способа кодирования:
Поскольку для русского языка, I1 (r) =4,356 бит, избыточность данного кода, согласно (2), составляет:
это означает, что при данном способе кодирования будет передаваться приблизительно на 12% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение K (2) = 4,716, что приI1 (e) = 4,036 бит приводят к избыточности кода Q (e) = 0,144.
Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления со списком кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Пример. Пусть имеется следующая таблица префиксных кодов:
| Таблица 2. Таблица кодов | |||||
| а | л | м | р | у | ы |
Требуется декодировать сообщение: 00100010000111010101110000110.
Декодирование производится циклическим повторением следующих действий.
1. Отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову.
2. Сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (1).
3. Декодировать рабочее кодовое слово, очистить его.
4. Проверить, имеются ли еще знаки в сообщении; если «да», перейти к (1).
Применение данного алгоритма дает:
Доведя процедуру до конца, получим сообщение: «мама мыла раму».
Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.
Из самой процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, не требуют разделителя. Средняя длина кода при этом оказывается:
Для сравнения можно найти I1 (A) – она оказывается равной 2,409, что соответствует избыточности кода Q = 0,0169, т.е. менее 2%.
Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.
Применение описанного метода для букв русского алфавита дает следующие коды:
| Таблица 3. Таблица кодов русских букв | |||||||
| Буква | Код | pi·10 3 | ki | Буква | Код | pi·10 3 | ki |
| пробел | я | ||||||
| о | ы | ||||||
| е | з | ||||||
| а | ь,ъ | ||||||
| и | б | ||||||
| т | г | ||||||
| н | ч | ||||||
| с | й | ||||||
| р | х | ||||||
| в | ж | ||||||
| л | ю | ||||||
| к | ш | ||||||
| м | ц | ||||||
| д | щ | ||||||
| п | э | ||||||
| у | ф |
Средняя длина кода оказывается равной K (2) = 4,395; избыточность кода Q (r) = 0,00887, т.е. менее 1%.
Таким образом, можно заключить, что существует метод построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) – нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.
2.1. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды
Параллельно должна решаться проблема различимости кодов. На выходе кодера получена следующая последовательность элементарных сигналов:
Каким образом она может быть декодирована? Если бы код был равномерным, приемное устройство просто отсчитывало бы заданное (фиксированное) число элементарных сигналов (например, 5, как в коде Бодо) и интерпретировало их в соответствии с кодовой таблицей. При использовании неравномерного кодирования возможны два подхода к обеспечению различимости кодов.
Неравномерный код с разделителем
В соответствии с перечисленными правилами строится кодовая табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 1.3) вероятностях появления отдельных букв.
Теперь по формуле нахождения среднего для значений случайных независимых величин можно найти среднюю длину кода К(r,2) для данного способа кодирования:
Поскольку для русского языка I1 ( r ) = 4,356 бит, избыточность данного кода, согласно (3.9), составляет:
это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение К(е,2) = 4,716, что при I1 ( e ) = 4,036 бит приводят к избыточности кода Q(е,2) = 0,168.
Рассмотрев один из вариантов двоичного неравномерного кодирования, необходимо ответить на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?
Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Пусть имеется следующая таблица префиксных кодов:
Требуется декодировать сообщение:
Декодирование производится циклическим повторением следующих действий:
(a) отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;
(b) сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (а);
(c) декодировать рабочее кодовое слово, очистить его;
(d) проверить, имеются ли еще знаки в сообщении; если «да», перейти к (а).
Применение данного алгоритма дает:
Рис. 3.1. Результат применения алгоритма
Доведя процедуру до конца, получается сообщение: «мама мыла раму».
Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.
Префиксный код Шеннона-Фано
Процедура построения кодов
Из процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, код является префиксным. Средняя длина кода равна:
I1 ( A ) = 2,390 бит. Подставляя указанные значения в (3.5), получается избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%. Однако, данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (0,35 и 0,65, соответственно). Применение изложенной схемы построения к русскому алфавиту дает избыточность кода 0,0147.
Префиксный код Хаффмана
Рис. 3.2. Процедура построения кодов
К(А,2) = 0,3 ∙ 2 + 0,2 ∙ 2 + 0,2 ∙ 2 +0,15 ∙ 3 + 0,1 ∙ 4 + 0,05 ∙ 4 = 2,45. (3.13)
Рис. 3.3. Обратная процедура построения кодов
Избыточность снова оказывается равной Q(A, 2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона-Фано становится очевидной, если сравнить избыточности кодов для какого-либо естественного языка. Применение описанного метода для букв русского алфавита порождает коды, представленные в табл. 3.4. (для удобства сопоставления они приведены в формате табл. 3.1).
Коды для букв русского алфавита
Средняя длина кода оказывается равной К(r,2) = 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано (см. выше).
Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.