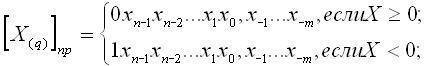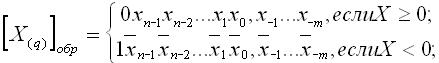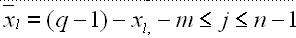операции с числами в специальных кодах

Операции с числами в специальных кодах

Арифметические операции на сумматорах прямого, обратного и дополнительного кода

Все операции в ЭВМ выполняют над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.

Каждому двоичному числу можно поставить в соответствие несколько видов кодов.

Различают следующие коды двоичных чисел: прямой (П), обратный (ОК) и дополнительный (ДК).

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом.

Прямой код двоичного числа образуется по следующему алгоритму:

1) определить данное двоичное число: либо целое (порядок), либо правильная дробь (мантисса);

2) если это дробь, то цифры после запятой можно рассматривать как целое число;

3) если это целое и положительное двоичное число, то вместе с добавлением нуля в старший разряд число превращается в код.

Для отрицательного двоичного числа перед ним ставится единица.

число Y ₂ = +0,11011012 → код числа Y _пр = 01101101.

Подчеркиванием выделяют знаковые разряды.

Обратный код двоичного числа образуется по следующему алгоритму:

1) обратный код положительных чисел совпадает с их прямым кодом;

2) обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются инверсными, т. е. нули заменяются единицами, а единицы нулями.

Свое название обратный код получил потому, что коды цифр отрицательного числа заменены инверсными.

Наиболее важные свойства обратного кода чисел:

— сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕ_ок = 1|1111, состоящую из единиц в знаковом и в значащих разрядах числа;

— нуль в обратном коде имеет двоякое значение.

Он может быть как положительным числом 0|0000, так и отрицательным 1|1111.

Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.

Обратный код положительного двоичного числа совпадает с прямым кодом, а для отрицательного числа нужно, исключая знаковый разряд, во всех остальных разрядах нули заменить единицами и наоборот.

Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2 0 – для целых чисел, 2 –k – для дробных).

Основные свойства дополнительного кода:

· сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:

т. е. число 10 (два) в знаковых разрядах числа;

Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется путем прибавления единицы к обратному коду.

Арифметические действия в машинных кодах

Сложение, а также вычитание чисел в обратном или дополнительном кодах выполняют с использованием обычного правила арифметического сложения многоразрядных чисел.

Это правило распространяется и на знаковые разряды чисел.

Различие обратного и дополнительного кодов связано с последующими действиями с единицей переноса из старшего разряда, изображающего знак числа.

При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда игнорируется, так как дополнительный код из обратного получается как раз прибавлением единицы.

Сложение и вычитание машинных чисел

Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.

Сложение (вычитание) машинных чисел

Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа.

Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей.

При выполнении сложения цифр необходимо соблюдать следующий алгоритм:

1) слагаемые должны иметь одинаковое число разрядов.

Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа;

2) знаковые разряды участвуют в сложении так же, как и значащие;

3) необходимые преобразования кодов производят с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу;

4) при преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом.

При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.

1. Сложить два числа: А₁₀ = 7, В₁₀ = 16.

Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:

Сложение в обратном или дополнительном коде дает один и тот же результат:

2. Сложить два числа: А₁₀ = +16, В₁₀ = –7 в ОК и ДК.

По таблице необходимо преобразование А +(–В), в которой второй член преобразуется с учетом знака:

При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда.

В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда.

В случае ДК этот перенос игнорируется.

Пример сложения чисел +18 и –7 приведен в таблице.

Источник

Обратный и дополнительный коды двоичных чисел

Пример перевода
x₁=10101-[x₁]_пр=010101
x₂=-11101-[x₂]_пр=111101
x₃=0,101-[x₃]_пр=0,101
x₄=-0,111-[x₄]_пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.

3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.

Пример перевода
x₁=10101-[x₁]_доп=010101
x₂=-11101-[x₂]_обр=100010+1-[x₂]_доп=100011
x₃=0,101-[x₃]_доп=0,101
x₄=-0,111-[x₄]_обр=1,000+1-[x₄]_доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.

Источник

Прямой, обратный и дополнительный коды двоичного числа

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

Прямой код

Обратный код

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

Арифметические операции с отрицательными числами в обратном коде:

Дополнительный код

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Арифметические операции с отрицательными числами в дополнительном коде

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

(34 голосов, оценка: 4,68 из 5)

Источник

Понятие о специальном кодировании чисел

Правило представления Q-ичного кода числа в прямом коде имеет вид:

где хi— значение цифры в i-м разряде исходного кода.

Здесь старший бит несет информацию о знаке числа. Если он принимает значение 0, то знак числа «+» ; если значение 1 — то знак числа «-».

Например, для двоичного кода

При представлении чисел в прямом коде реализация арифметических операций в ЭВМ должна предусматривать различные действия с модулями чисел в зависимости от их знаков. Так, сложение в прямом коде чисел с одинаковыми знаками выполняется достаточно просто. Числа складываются и сумме присваивается код знака слагаемых. Значительно более сложной является операция алгебраического сложения в прямом коде чисел с различными знаками. В этом случае приходится определять большее по модулю число, производить вычитание чисел и присваивать разности знак большего по модулю числа. Для упрощения выполнения операций алгебраического сложения в ЭВМ используются специальные коды, позволяющие свести эту операцию к операции арифметического сложения. В качестве специальных в ЭВМ применяются обратный и дополнительный коды. Они образуются из прямых кодов чисел, причем специальный код положительного числа равен его прямому коду.

Для обозначения обратного кода числа Х(q) используется запись вида [Х(q)]_обр.
Правило представления q-ичного кода числа в обратном коде имеет вид:

где: q — основание системы счисления;
xj значение цифры в i-ом разряде исходного кода.

Для двоичной системы счисления, если х = 1, то 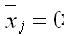и наоборот. Отсюда можно сформулировать частное правило образования обратного кода для отрицательных двоичных чисел.

Для преобразования прямого кода двоичного отрицательного числа в обратный код и наоборот необходимо знаковый разряд оставить без изменения, а в остальных разрядах нули заменить на единицы, а единицы на нули.

Таким образом, для преобразования прямого кода q-ичного отрицательного числа в дополнительный необходимо образовать его в обратный код и в младший разряд добавить единицу.

Например, для двоичных чисел:

При выполнении операции алгебраического сложения перед преобразованием прямых кодов слагаемых в специальные необходимо их выровнять по числу разрядов, если число разрядов слагаемых различно. Кроме того, в некоторых случаях может произойти переполнение разрядов сетки. Признаком переполнения разрядной сетки является следующая комбинация цифр в знаковых разрядах слагаемых и результата:

Результат сложения специальных кодов чисел при переполнении разрядной сетки является неверным.

Источник

Использование специальных кодов при выполнении операций сложения и вычитания чисел в естественной форме

Понятие кодов в цифровых системах (ЦС).

В ЦС, с целью упрощения устройств, выполняющих арифметические операции, применяют специальные коды для представления чисел, в которых для изображения числа и его знака используются цифры двоичной системы счисления. К таким кодам относят прямой, обратный и дополнительный коды, которые называют ещё машинными кодами чисел.

Специальное кодирование чисел

Известно, что при представлении чисел в прямом коде реализация операций сложения и вычитания в ЦС должна предусматривать различные действия с модулями чисел в зависимости от их знаков. Сложение в прямом коде с одинаковыми знаками выполняется достаточно просто. Числа складываются и сумме присваивается код знака слагаемых. Значительно более сложной является операция алгебраического сложения прямых кодов чисел с различными знаками. В этом случае приходится определять большее по модулю число, производить вычитание чисел и присваивать коду разности знак большего по модулю числа. Для упрощения выполнения операции алгебраического сложения чисел в ЦС, в частности в ЭВМ, используются специальные коды, позволяющие свести эту операцию к операции арифметического сложения специальных кодов. В качестве специальных в ЭВМ применяются обратный и дополнительный коды. Для представления чисел в специальном коде используется дополнительный разряд с определенным весом. В качестве дополнительного обычно используется знаковый разряд прямого кода.

Правило 1.Специальный код положительного числа совпадает с его прямым кодом и, наоборот, прямой код положительного числа совпадает с его специальным кодом.

Обратный код числа

Для двоичного числа можно сказать, что обратный код, это специальный код, инвертированный во всех разрядах, кроме знакового

Правило 2. Для преобразования q-ичного кода или прямого q-ичного кода отрицательного числа в обратный код или наоборот для преобразования обратного кода отрицательного числа в прямой код необходимо в дополнительный (знаковый) разряд записать цифру 1, а в цифровые разряды записать коэффициенты x_i, определяемые из соотношения:

Пример 1.21. Образовать обратные коды чисел:

Решение. 1. Поскольку числа положительные, то в соответствии с правилом 1 их обратные коды равны прямым кодам: [X₁₀]_ок = 0.95.28; [X₁₆]_ок = 0.A5.1C; [X₈]_ок = 0.63.27; [X₂]_ок=0.101.011.

2. Так как числа отрицательные, то в соответствии с правилом 2 их обратные коды равны:

Пример 1.22. Образовать прямые и q-ичные коды чисел, если их обратные коды равны:

Решение. 1. Так как исходные коды положительные, то в соответствии с правилом 1:

2. Поскольку исходные коды отрицательные, то в соответствии с правилом 2 [X₁₀]_пк=1.24.73; X₁₀=-24,73; [X₁₆]_пк=1.AB.5A; X₁₆=-AB,5A; [X₈]_пк =1.40.52; X₈=-40,52; [X₂]_пк=1.110.01; X₂=-110,01. Поскольку для двоичной СС (q-1)=1, то из правила 2 следует частное правило преобразования кодов двоичных чисел в обратные коды и наоборот.

Правило 3. Для преобразования двоичного кода или прямого кода двоичного отрицательного числа в обратный код и наоборот для преобразования обратного кода отрицательного числа в прямой код, необходимо в дополнительный (знаковый) разряд записать цифру 1 и во всех цифровых разрядах заменить нули на единицы, а единицы на нули.

Таким, образом, из правила 3 следует, что для образования обратного кода отрицательного двоичного числа необходимо заменить значения цифровых разрядов на обратные. Это и обусловило название этого специального кода.

Дополнительный код

Служит для унификации операций сложения и вычитания.

Другими словами, дополнительный код, это дополнение кода отрицательного числа до основания q (Например, для двоичного числа дополнение до основания 2. В результате каждый разряд отрицательного числа инвертируем, а к последнему разряду добавляем 1).

Правило 4. Для преобразования q-ичного кода или прямого q-ичного кода отрицательного числа в дополнительный код или наоборот для преобразования дополнительного кода отрицательного числа в прямой код необходимо в дополнительный (знаковый) разряд записать цифру 1, а в цифровые разряды записать коэффициенты x_i, определяемые из соотношений:

Из определения дополнительного кода и правила 4 видно, что дополнительный код отрицательного числа отличается от обратного на единицу младшего разряда.

Пример 1.23. Образовать дополнительные коды чисел:

Решение. 1. Поскольку числа положительные, то в соответствии с правилом 1 их дополнительные коды равны прямым кодам:

2. Так как числа отрицательные, то в соответствии с правилом 4 их дополнительные коды равны:

Пример 1.24. Образовать прямые и q-ичные коды чисел, если:

Решение. Поскольку исходные коды отрицательны, то в соответствии с правилом 4: [X₁₀]=1.45.9 и X₁₀=-45,92; [X₁₆]_пк=1.A5.4E и X₁₆=-A5,4E; [X₈]_пк=1.21.53 и X₈ =-21,53; [X₂]_пк=1.100.11 и X₂=-100,11.

Заметим, что специальные коды не изменяют значения числа.

(1.28)

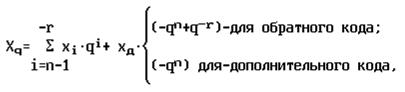
Значение числа X_q можно определить по его специальному коду, если воспользоваться выражением (1.28), где x_д— значение дополнительного разряда специального кода; x_i— значение i-го цифрового разряда специального кода.

Решение. Пользуясь выражением (1.28) и учитывая, что для данного примера n = r = 2, получим:

Таким образом, дополнительный код двоичного числа образуется из прямого кода инверсией и добавлением единицы к младшему разряду. Если результат получился отрицательным, то чтобы получить прямой код необходимо осуществить инверсию, а затем добавить единицу к младшему разряду. Единица переполнения знакового разряда при использовании дополнительного кода отбрасывается.

Использование специальных кодов при выполнении операций сложения и вычитания чисел в естественной форме

Специальные коды используются для осуществления операций сложения и вычитания.

Однако, при осуществлении указанных операций происходит переполнение разрядной сетки, в результате чего получаем ошибку. Для устранения данного недостатка используют модифицированный специальные коды.

Дата добавления: 2017-11-21 ; просмотров: 609 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник