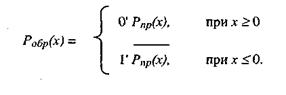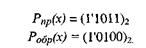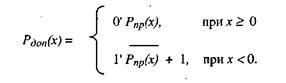особенности представления чисел в эвм прямой обратный дополнительный коды

Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:

Рассмотрим разные методы представления.

Содержание

Прямой код [ править ]

Достоинства представления чисел с помощью прямого кода [ править ]

Недостатки представления чисел с помощью прямого кода [ править ]

Из-за весьма существенных недостатков прямой код используется очень редко.

Код со сдвигом [ править ]

По сути, при таком кодировании:

Достоинства представления чисел с помощью кода со сдвигом [ править ]

Недостатки представления чисел с помощью кода со сдвигом [ править ]

Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.

Дополнительный код (дополнение до единицы) [ править ]

В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).

Алгоритм получения кода числа:

Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]

Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]

Дополнительный код (дополнение до двух) [ править ]

Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).

Алгоритм получения дополнительного кода числа:

Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]

Достоинства представления чисел с помощью кода с дополнением до двух [ править ]

Недостатки представления чисел с помощью кода с дополнением до двух [ править ]

Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.

Источник

Особенности представления чисел в ЭВМ: прямой, обратный, дополнительный коды.

Представление чисел в формате с фиксированной запятой. Представление чисел в формате с плавающей запятой.

Представление чисел в формате с фиксированной запятой. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «запятая» «находится» справа после младшего разряда, то есть вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2 = = 111100002 будет храниться в ячейке памяти следующим образом:

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно

Диапазон изменения целых неотрицательных чисел чисел: от 0 до 255.

Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа. Например, число 200210 = 111110100102 будет представлено в 16-разрядном представлении следующим образом:

Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:

Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.

Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен

Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, так как в n-разрядной компьютерной арифметике:

поскольку в компьютерной n-разрядной арифметике 2n = 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей.

Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

1. Модуль числа записать в прямом коде в n двоичных разрядах.

2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).

3. К полученному обратному коду прибавить единицу.

Представление чисел в формате с плавающей запятой. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. В этом случае положение запятой в записи числа может изменяться.

Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде:

Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:

Здесь нормализованная мантисса: m = 0,55555, порядок: n = 3.

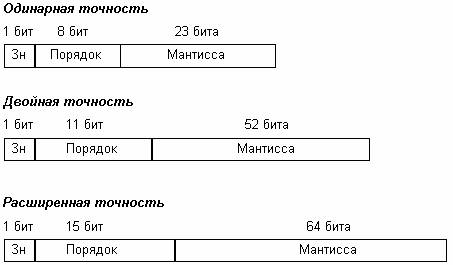
Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.

Максимальное значение порядка числа составит 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа составит:

Максимальное значение положительной мантиссы равно:

Таким образом максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 × 10 38 (количество значащих цифр десятичного числа в данном случае ограничено 7 разрядами).

Основные логические операции: конъюнкция, дизъюнкция, инверсия. Таблицы истинности. Аксиомы и законы алгебры логики. Преобразование логических выражений. Базовые логические элементы. Логические (комбинационные) схемы. Минимизация логических функций.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Что же такое логическое высказывание?

Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:

НЕ Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ). Высказывание истинно, когда A ложно, и ложно, когда A истинно. Пример. «Луна — спутник Земли» (А); «Луна — не спутник Земли» ( ).

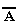
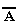
ИЛИ Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3» — истинны.

Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: «данный четырёхугольник — квадрат» (А) и «около данного четырёхугольника можно описать окружность» (В). Рассмотрим составное высказывание , понимаемое как «если данный четырёхугольник квадрат, то около него можно описать окружность». Есть три варианта, когда высказывание истинно:

Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.

. Высказывание истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 3», «23 делится на 6 тогда и только тогда, когда 23 делится на 3» истинны, а высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 5», «21 делится на 6 тогда и только тогда, когда 21 делится на 3» ложны.

Высказывания А и В, образующие составное высказывание , могут быть совершенно не связаны по содержанию, например: «три больше двух» (А), «пингвины живут в Антарктиде» (В). Отрицаниями этих высказываний являются высказывания «три не больше двух» ( ), «пингвины не живут в Антарктиде» ( ). Образованные из высказываний А и В составные высказывания A B и истинны, а высказывания A и B — ложны.

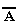
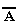
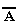
Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.

Импликацию можно выразить через дизъюнкцию и отрицание: А В = v В.

Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

Дата добавления: 2019-03-09 ; просмотров: 856 ; Мы поможем в написании вашей работы!

Источник

Представление чисел в ЭВМ

Целые числа

Для числа +1101 :

Вещественные числа (числа с плавающей точкой)

0.15625 = 00101₂
446.15625 = 110111110,00101₂ = 1,1011111000101*2 8

Знак S = 0
Порядок P = 8 + 1023 = 1031₁₀ = 10000000111₂
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE28000000000₁₆

455,375 = 111000111,0110₂ = 1,110001110110*2 8 ₂

Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101

1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881

б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011

1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818

Источник

Представление чисел в ЭВМ. Прямой, обратный и дополнительный коды.(Лекция 4)

В ВТ, с целью упрощения реализации арифметических операций, применяют специальные коды. За счет этого облегчается определение знака результата операции, а операция вычитания чисел сводится к арифметиче­скому сложению. В результате упрощаются устройства, выполняющие арифметические операции.

В ВТ применяют прямой, обратный и дополнительный коды.

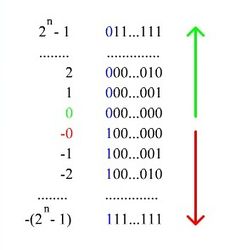
Прямойдвоичный код Рпр(х) — это такое представление двоичного числа х, при котором знак «+» кодируется нулем в старшем разряде числа, а знак «-» — единицей. При этом старший разряд называется знаковым.

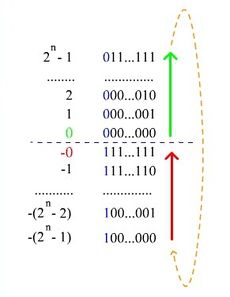
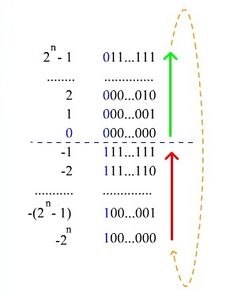
Обратный кодРобр(х) получается из прямого кода по следующему правилу:

Из приведённого выражения видно, что обратный код для положительных чисел совпадает с прямым кодом. Чтобы представить отрицательное двоичное число в обратном коде, нужно оставить в знаковом разряде 1, во всех значащих разрядах заменить 1 на 0, а 0 на 1. Такая операция называется инвертированием и обозначается горизонтальной чертой над инвертируемым выражением

Считается, что здесьчисла представлены пятью разрядами. Из рассмотренного примера видно, что обратный код для положительных чисел совпадает с прямым, а для отрицательных чисел получается инверсией (переворотом) всех разрядов, кроме знакового разряда.

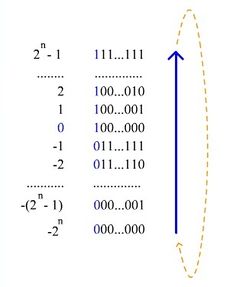
Дополнительный кодРдоп(х) образуется следующим образом:

Из выражения видно, что дополнительный код положительного числа совпадает с прямым кодом, а для отрицательного числа получается инверсией всех значащих разрядов и добавлением единицы к младшему разряду результата.

Дополнительный код отрицательного числа может быть получен из обратного кода путем прибавления 1 к младшему разряду обратного кода (естественно, с учетом переносов между разрядами).

Пример5. Получить дополнительный код для числа

Pnp(x) = (1’1101)прямой код

Робр(х) =(1’0010) обратный код

Рдоп(х ) = (1’0011) дополнительный код.

При алгебраическом сложении двоичных чисел положительныеслагаемые представляют в прямом коде, а отрицательные — в дополнительном коде и производят арифметическое суммирование этих кодов,включая разряды знаков, которые при этом рассматривают как старшиеразряды. При возникновении переноса из разряда знака единицу переноса отбрасывают, в результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном коде,если сумма отрицательная.

Необходимо найти сумму: у = х1 + х2.

Учитывая, что х1>0, это число нужно представить в прямом коде, а так как х2

Источник

Прямой, обратный и дополнительный коды двоичного числа

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

Прямой код

Обратный код

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

Арифметические операции с отрицательными числами в обратном коде:

Дополнительный код

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Арифметические операции с отрицательными числами в дополнительном коде

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

(34 голосов, оценка: 4,68 из 5)

Источник