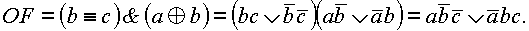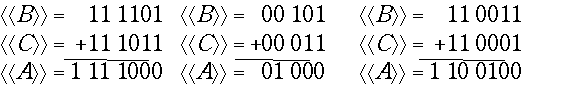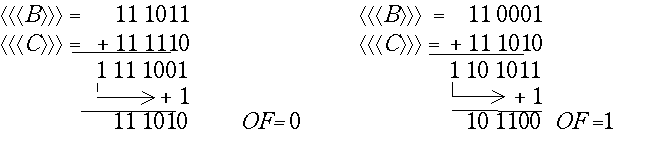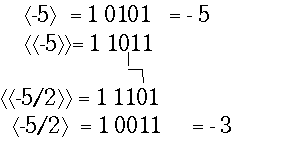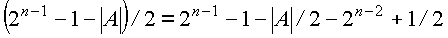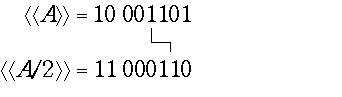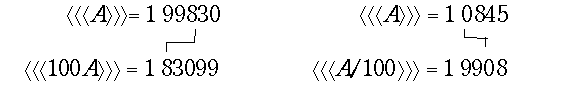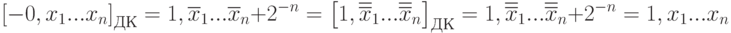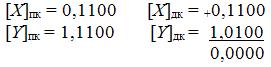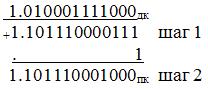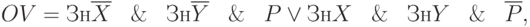переполнение в дополнительном коде
Переполнение в дополнительном коде
Переполнение разрядной сетки в любом случае является грубой ошибкой и непременно должно обнаруживаться аппаратными средствами. Проще всего контролируется переполнение при сложении прямых кодов. При сложении прямых кодов переносы в знаковый разряд вообще не должны происходить, поэтому возникновение такого переноса можно использовать как признак переполнения.
При сложении дополнительных или обратных кодов перенос в знаковый разряд сам по себе не является признаком переполнения. Для контроля переполнения здесь можно применить один из трех способов:
Этот способ не может быть применен, в частности, при одноадресном сложении из-за невозможности одновременного чтения знаковых цифр обоих операндов;
В первом примере переполнения нет, а во втором и третьем наблюдается переполнение. Выходящие из разрядной сетки цифры переносов из старшего знакового разряда (первый и третий примеры) игнорируются, как и вообще при сложении дополнительных кодов.
Логический признак переполнения при этом способе выражается как
;
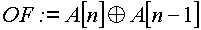
Необходимо различать сдвиг кода и сдвиг арифметический. Сдвиг кода или логический сдвиг выполняется просто. Сдвигаются все цифры, освободившиеся разряды занимаются нулями.
В арифметическом сдвиге знаковый разряд не участвует, он сохраняет свою прежнюю цифру. Таким образом, умножается или делится на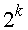 
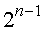
только модуль числа (или его дополнение до 
). Крайние цифры модуля теряются. Если число положительно, то освободившиеся разряды занимаются нулями. Если же оно отрицательно, то освободившиеся разряды занимаются по-разному в зависимости от принятого кода и от направления сдвига. Соответствующие правила сведены в таблицу 4.1.
Докажем необходимость именно такого выполнения арифметического сдвига над дополнительным и обратным кодами отрицательных чисел.
Сдвиг дополнительного кода на один разряд вправо, то есть деление дополнения модуля числа на два можно описать формулой
.
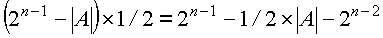
Первые два члена правой части равенства как раз дают верное изображение дополнения. Третий член означает нехватку единицы старшего разряда модуля. Чтобы скомпенсировать эту нехватку нужно, согласно таблице, вписать единицу в освободившийся слева разряд.
Соответствующая формула для обратного кода:
.
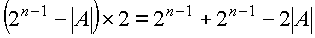
Первая из единиц с весом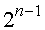 
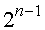
выдвигается из разрядной сетки модуля и теряется, остается дополнение 2| A | до , что и требовалось. Коррекция не нужна.
В обратном коде соответственно получится
.
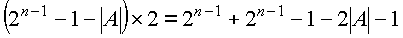
Первый член формулы, как и в дополнительном коде, теряется. Но в младшем разряде обнаруживается нехватка единицы. Чтобы результат получился верным, необходимо в младший разряд при каждом сдвиге влево вписывать единицу.
Если сдвигаемое число представлено в модифицированном коде (дополнительном или обратном), то арифметический сдвиг выполняется особенным образом и называется модифицированным сдвигом. Старшая из знаковых цифр остается на прежнем месте, а младшая участвует в сдвиге вместе с цифрами дополнения. Такая организация сдвига позволяет сохранить верный знак числа и восстановить правильное представление числа. Пример арифметического сдвига вправо:
Расположение запятой не влияет на правила выполнения сдвигов. Над правильными или неправильными дробями сдвиги выполняются точно так же, как над целыми числами. При других основаниях системы счисления сдвиги выполняются аналогично, только вместо единицы для заполнения освободившихся разрядов берется старшая из допустимых цифр. Примеры арифметического сдвига десятичных дробей:
Арифметический сдвиг и сдвиг кода могут выполняться как элементарные операции в составе микропрограмм умножения и деления, а также и самостоятельно, как операции ассемблера, доступные программисту. В дополнение к описанным в данной лекции видам сдвигов (логический сдвиг SHL и SHR и арифметический SAL и SAR ) ассемблер содержит еще команды циклического сдвига: ROL и ROR и циклического сдвига через триггер переноса: RCL и RCR.
Переполнение разрядной сетки
В ЭВМ количество разрядов, используемых для представления чисел, ограничено. Поэтому при сложении двух чисел с одинаковыми знаками их сумма может оказаться больше по модулю, чем максимальное число, которое может быть записано при заданном количестве разрядов и результат сложения окажется неверным. Такое явление называется переполнением разрядной сетки.
Пример 6. Сложить два числа А = + 1101,1 и В = + 1011,0 (n=4, m=1) в обратном коде.
Решение. [A]обр = 0.1101,1
В этом примере 1 переноса из старшего разряда попадает в знаковый разряд ( с отрицательным весом) и, следовательно, в результате сложения двух положительных чисел получается отрицательное число.
При сложении отрицательных чисел в обратном или дополнительном кодах переполнение разрядной сетки наступает в том случае, если отсутствует 1 переноса в разряд с отрицательным весом и результат оказывается положительным.
Пример 7. Сложить два числа А = — 1011 и В= — 1101 (n=4, m=0) в дополнительном коде.
Решение: [A]доп = 1.0101
Для обнаружения переполнения разрядной сетки используют следующие способы:
1. Сравнивают знаки слагаемых со знаком суммы. Сигнал переполнения вырабатывается тогда, когда знаки слагаемых одинаковы и не совпадают со знаком суммы.
2. Второй способ основан на применении модифицированных кодов. Модификация кодов заключается во введении дополнительного разряда, который располагается перед знаковым. Этот разряд часто называют разрядом переполнения. Иногда говорят, что модифицированные коды содержат два знаковых разряда. Положительные числа имеют в знаковых разрядах два нуля, отрицательные – две единицы. При использовании модифицированных обратного и дополнительного кодов признаком переполнения разрядной сетки является наличие в знаковых разрядах различных цифр 01 или 10.
В обоих примерах произошло переполнение разрядной сетки.
При несовпадении знаковых разрядов в модифицированных кодах вырабатывается сигнал переполнения разрядной сетки.
Порядок выполнения работы
Содержанием работы является: 2 схемы одноразрядных двоичных сумматоров, схема 8-ми разрядного двоичного сумматора параллельного действия, построение схем с использованием программы«ЕВЕМА-2» и контроль правильности их работы.
Работу рекомендуется выполнять в следующей последовательности:
— по таблице истинности одноразрядного двоичного сумматора получить выражения для сигналов суммы и переноса в булевом базисе;
— набрать на компьютере комбинационную схему одноразрядного двоичного сумматора;
— набрать на компьютере комбинационную схему 8-ми разрядного двоичного сумматора;
— выполнить сложение заданных чисел в обратном и дополнительном кодах;
— проверить правильность работы схемы, задавая на ее входах значения чисел в обратном и дополнительном кодах.
Статьи к прочтению:
Разрядная сетка с фиксированной запятой
Похожие статьи:
РЕЖИМ ПОСТРОЕНИЯ ПО СЕТКЕ Когда Вы работаете с чертежом, иногда бывает удобно включить изображение сетки на экране и назначить привязку к ее узлам. При…
КУРСОВАЯ РАБОТА По дисциплине «Операционные системы» Исполнитель: ст. гр. 4301 Галиева Д.М. Руководитель: Шалагин С. В. Оценка_________________…
Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах
Дополнительный код
Здесь связь между числом X и его изображением в дополнительном коде [Х]дк определяется следующим равенством.
Положительное число в дополнительном коде выглядит так же, как и в прямом и обратом кодах, то есть для X > 0 справедливо утверждение:
Получение дополнительного кода отрицательного числа осуществляется в соответствии с равенством:
Обратное преобразование отрицательного числа (от дополнительного к прямому) выполняется следующим образом.
Например [[- 0,1101]дк = 1,0011]дк = 1,1101, то есть от дополнительного кода берется дополнительный код.
Рассмотрим четыре случая:
[Х]дк + [Y]дк = X + (2 + Y) = 2 + (X + Y) – предварительный результат.
Правильный результат при Х + Y > 0 равен X + Y.
Выполняется коррекция, равная вычитанию 2 из предварительного результата (исключение в нем единицы с весом 2 1 ).
Методика выполнения операции не изменяется, когда [Х]дк + [Y]дк = 0.
То есть ноль в дополнительном коде ноль имеет единственное представление.
Достоинства операций суммирования чисел в обратном и дополнительном кодах:
Недостаток: невозможно фиксировать переполнение.
Для быстрого перевода числа из прямого кода в дополнительный или наоборот, из дополнительного кода в прямой можно воспользоваться очень простым правилом.
Как уже указывалось, положительные числа в прямом и дополнительном кодах записываются одинаково. Так что здесь никаких проблем не возникает.
Для отрицательных чисел при переводе можно воспользоваться следующим правилом. Знак отрицательного числа, единица, естественно, сохраняется. А цифровые разряды меняются слева направо на противоположные до последней единицы в числе. Последняя единица и все следующие за ней разряды сохраняются:
Это правило вытекает из общего механизма перевода отрицательных чисел из прямого кода в дополнительный и наоборот. Первый шаг такого действия – инвертирование всех разрядов цифровой части (напомним, речь идет об отрицательных числах). При этом стоящие в конце числа нули станут единицами. На втором шаге к младшему разряду полученного результата добавляется единица. Это вызовет перенос, который будет распространяться до того разряда, который в новом числе равен нулю, а в исходном, следовательно, равен единице. Преобразование закончено.
Методы фиксации переполнения при алгебраическом суммировании чисел с фиксированной запятой в обратном и дополнительном кодах
Фиксация переполнения по знаку результата
Прежде всего, отметим, что переполнение разрядной сетки при суммировании чисел с фиксированной запятой возможно лишь для операндов, имеющих одинаковые знаки, так как, в противном случае, модуль результата окажется меньше модуля любого из операндов и, следовательно, переполнения не будет.
В связи с этим, факт наличия переполнения достаточно просто определить по изменению знака результата по сравнению со знаками операндов:
где P – перенос за пределы знакового разряда.
Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах
Дополнительный код
Здесь связь между числом X и его изображением в дополнительном коде [Х]дк определяется следующим равенством.
Положительное число в дополнительном коде выглядит так же, как и в прямом и обратом кодах, то есть для X > 0 справедливо утверждение:
Получение дополнительного кода отрицательного числа осуществляется в соответствии с равенством:
Обратное преобразование отрицательного числа (от дополнительного к прямому) выполняется следующим образом.
Например [[- 0,1101]дк = 1,0011]дк = 1,1101, то есть от дополнительного кода берется дополнительный код.
Рассмотрим четыре случая:
[Х]дк + [Y]дк = X + (2 + Y) = 2 + (X + Y) – предварительный результат.
Правильный результат при Х + Y > 0 равен X + Y.
Выполняется коррекция, равная вычитанию 2 из предварительного результата (исключение в нем единицы с весом 2 1 ).
Методика выполнения операции не изменяется, когда [Х]дк + [Y]дк = 0.
То есть ноль в дополнительном коде ноль имеет единственное представление.
Достоинства операций суммирования чисел в обратном и дополнительном кодах:
Недостаток: невозможно фиксировать переполнение.
Для быстрого перевода числа из прямого кода в дополнительный или наоборот, из дополнительного кода в прямой можно воспользоваться очень простым правилом.
Как уже указывалось, положительные числа в прямом и дополнительном кодах записываются одинаково. Так что здесь никаких проблем не возникает.
Для отрицательных чисел при переводе можно воспользоваться следующим правилом. Знак отрицательного числа, единица, естественно, сохраняется. А цифровые разряды меняются слева направо на противоположные до последней единицы в числе. Последняя единица и все следующие за ней разряды сохраняются:
Это правило вытекает из общего механизма перевода отрицательных чисел из прямого кода в дополнительный и наоборот. Первый шаг такого действия – инвертирование всех разрядов цифровой части (напомним, речь идет об отрицательных числах). При этом стоящие в конце числа нули станут единицами. На втором шаге к младшему разряду полученного результата добавляется единица. Это вызовет перенос, который будет распространяться до того разряда, который в новом числе равен нулю, а в исходном, следовательно, равен единице. Преобразование закончено.
Методы фиксации переполнения при алгебраическом суммировании чисел с фиксированной запятой в обратном и дополнительном кодах
Фиксация переполнения по знаку результата
Прежде всего, отметим, что переполнение разрядной сетки при суммировании чисел с фиксированной запятой возможно лишь для операндов, имеющих одинаковые знаки, так как, в противном случае, модуль результата окажется меньше модуля любого из операндов и, следовательно, переполнения не будет.
В связи с этим, факт наличия переполнения достаточно просто определить по изменению знака результата по сравнению со знаками операндов:
где P – перенос за пределы знакового разряда.
Переполнение в дополнительном коде
В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительных кодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.
Сложение обратных кодов. Здесь при сложении чисел А и В имеют место четыре основных и два особых случая:
1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:
Получен правильный результат.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
4. А и В отрицательные. Например:
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.
Сложение дополнительных кодов. Здесь также имеют место рассмотренные выше шесть случаев:
1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:
Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
4. А и В отрицательные. Например:
Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.
Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.