перевести двоичный код в двоично десятичный код
Двоично-десятичное кодирование
Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот.
После калькулятора Перевод дробных чисел из одной системы счисления в другую я думал, что тема с системами счисления уже закрыта. Но, как оказалось, еще нет.
Как я писал по ссылке выше, основная проблема при переводе дробных чисел из одной системы счисления в другую это потеря точности, когда, например, десятичное число 0.8 нельзя перевести в двоичное без погрешности.
Поскольку десятичные числа активно используются человеком, а двоичные — компьютером, этой проблемой в применении к двоичной и десятичной системам однажды уже озаботились какие-то светлые умы и придумали двоично-десятичное кодирование (binary coded decimal, BCD). Суть идеи проста — берем и для каждой десятичной цифры заводим байт. И в этом байте тупо пишем значение десятичной цифры в двоичном коде. Тогда число, например, 0.8 будет 0.00001000. Потом, правда, подумали еще, и решили, что раз уж верхняя часть байта всегда пустует (так как максимум 9 — это 1001), то давайте для каждой десятичной цифры заводить полубайт. И назвали это упакованным двоично-десятичным кодированием (packed BCD).
В упакованном кодировании наше 0.8 будет 0.1000, а какое-нибудь 6.75 будет 0110.01110101.
Прекрасная идея, конечно. Точность не теряется, человек может двоичные числа переводить в десятичные и наоборот прямо на лету, округлять можно, откидывая лишнее. Но как-то не получила она широкого распространения, потому как жизнь машинам она, наоборот, усложняла — и памяти для хранения чисел надо больше, и операции над числами реализовать сложнее. Так и осталась забавным курьезом, и я бы ничего о ней не знал, если бы пользователи не подсказали, что есть такая.
Ну и небольшой калькулятор по этому поводу — вводим либо десятичное число, либо двоичное, подразумевая, что это упакованный двоично-десятичный код, и получаем результат. Понятно, что все преобразования можно проделать и в уме, и в этом ее преимущество; но зачем же лишний раз мозги напрягать, верно?
Конвертер величин
Конвертер чисел в различных системах счисления.
Передача данных
Подробнее о числах
Общие сведения
Число — это абстрактное математическое понятие обозначающее количество. Числа используются для счета. Числа использовались человеком с древнейших времен, вначале в виде счетных палочек или зарубок и черточек на дереве и кости, а потом и в виде более абстрактных систем. Существует много способов выражения чисел и работы с ними; некоторые из них приведены ниже. Системы счисления эволюционировали на протяжении многих веков и не все из них используются по сей день.
Различные способы представления чисел
Ученые считают, что понятие числа возникло в разных культурах независимо. Символы для обозначения цифр в письменном виде также возникли в каждой культуре отдельно, но постепенно, с развитием торговли, люди начали обмениваться идеями и заимствовать друг у друга принципы счисления или написания чисел. Поэтому те системы счисления, которыми мы сейчас пользуемся, создавались коллективно многими народами.
Арабские цифры
Арабская система счисления — одна из самых широко используемых систем счисления. Она была заимствована из Индии и доработана персидскими и арабскими математиками. В русском языке эта система называется в основном «арабской», но на других языках, например английском, она чаще называется «индо-арабской». В средние века, особенно ближе к середине и концу этого периода, торговля распространилась по всему миру, и купцы стали привозить в другие страны не только товары, но и сведения о науках, таких как математика. Благодаря этому арабские цифры начали использовать в Европе, сначала в монастырях, а позже и в светском обществе. Папа римский Сильвестр II одним из первых стал использовать и распространять арабские цифры взамен римских, познакомившись с ними благодаря связям с арабскими государствами на территории нынешней Испании. Европейские ученые приспособили и частично изменили написание цифр, и арабская система счисления получила широкое применение не только во всей Европе, но и по всему миру благодаря торговле и во время колонизации других континентов. Арабская система — десятичная, то есть с основанием 10 и с использованием десяти цифр, которыми можно выразить все возможные числа.
Десять — одно из наиболее широко используемых чисел в системах счета, и десятичная система распространена во многих странах. Это связано с тем, что издревле люди пользовались десятью пальцами на руках для счета. До сих пор люди, которые учатся считать или хотят проиллюстрировать пример, связанный со счетом, используют пальцы. Существуют даже такие выражения как «считать на пальцах». В некоторых культурах для счета использовали также и пальцы ног, костяшки пальцев, и даже пространство между пальцами. Интересно, что во многих языках слово, обозначающее пальцы и цифры — одно и то же. Например, в английском, это слово — «digit» (произносится как «диджит»).
Римские цифры
Римские цифры использовались в Древнем Риме и Европе примерно до четырнадцатого столетия. Их до сих пор используют в некоторых контекстах, например на циферблатах часов, в именах Папы Римского, в названиях повторяющихся событий, например, олимпийских игр, и так далее. Римская система счисления использует семь букв латинского алфавита для обозначения всех возможных комбинаций чисел:
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Порядок написания цифр важен потому, что большее число слева от меньшего значит, что оба числа необходимо сложить, в то время как меньшее число слева от большего следует вычесть из большего числа. Например, XI равняется одиннадцати, а IX — это 9. Это правило действует только для чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях эти правила не соблюдаются, и числа пишутся в ряд, например XXXXX.
Системы счисления в других культурах
Во многих культурах использовались системы счисления, похожие на римскую и арабскую. Например, в кириллической системе счисления цифры от одного до девяти, десять, и кратные ста писались буквами кириллицы. Также существовал специальный знак, похожий на тильду «
», который писали над такими цифрами, чтобы показать, что это не буквы. Существовала похожая система и с использованием глаголицы. В еврейской системе счисления буквами еврейского алфавита записывали числа от одного до десяти, кратные десяти, сто, двести, триста, и четыреста. Остальные числа писали как сумму или произведение. Греческая система счисления также похожа на все, приведенные выше.
В некоторых культурах системы счисления были проще. Например, вавилонские цифры можно было записать с помощью двух клинописных знаков, обозначавших единицу (похожего на большую букву «Т») и десять (похожего на букву «С»). Так, например, 32 можно записать как «СССТТ», используя соответствующие знаки. Египетская система счисления похожа, только в ней существовали также символы для нуля, сотни, тысячи, десяти тысяч, ста тысяч и миллиона, а также были специальные знаки для записи дробей. Цифры майя записывались с помощью знаков, обозначавших ноль, единицу и пятерку. Числа выше девятнадцати также имели своеобразное написание. В них использовались знаки для одного и пяти, но с другим расположением, чтобы показать, что значение этих цифр — другое.
Единичная система счисления
В единичной или унарной системе счисления используется только один знак, обозначающий единицу. Каждое число записывается с помощью таких знаков, количество которых равно этому числу. Например, если такой знак — буква «А», то число пять можно записать как «ААААА». Унарная система часто используется учителями, которые учат детей считать, потому что она помогает детям понять зависимость между количеством предметов, например счетных палочек или карандашей, и более абстрактного понятия числа. Часто унарную систему используют во время игр, чтобы записывать очки, набранные командами, или для счета дней или предметов. Причем метод записи в разных культурах отличается. Например, во многих странах, где принят латинский алфавит, чаще используются черточки. Обычно четыре вертикальные черточки перечеркивают горизонтальной или диагональной, и продолжают счет с новой группы черточек. В примере А) на рисунке счет доходит до четырех, эти черточки перечеркивают пятой, дальше добавляют еще пять черточек, и опять начинают новый ряд. Так, счет доходит до двенадцати. В странах, где в языке используют или использовали китайские иероглифы, люди обычно рисуют не четыре черточки, перечеркнутые пятой, а специальный иероглиф из пяти штрихов. Последовательность этих штрихов не произвольная, а установлена правилами правописания. В примере В) на рисунке счет доходит то пяти и человек пишет два первых штриха следующего иероглифа, заканчивая счет на семи. Кроме простого счета и учета, унарную систему также используют в компьютерных технологиях и электронике.
Позиционная система счисления
В позиционной системе счисления значение каждого знака, обозначающего цифру, зависит от его положения в числе. Это значение также зависит от основания системы счисления. Позиция обычно называется разрядом. Например, число 101 в двоичной системе не равно ста одному в десятичной. Рассмотрим позиционную систему на примере десятичной:
Чтобы получить значение числа, складывают все числа, полученные выше, то есть значения чисел в каждом разряде. Такой способ написания чисел позволяет работать с большими числами, и не занимает так много места в тексте, по сравнению с непозиционными системами счисления.
Пример использования позиционирования в десятичной системе: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная система
Двоичная система очень широко используется в математике и вычислительной технике. Все возможные числа представлены в ней с помощью только двух цифр, «0» и «1», хотя в некоторых случаях используют и другие знаки, например «+», «–». При переводе чисел из десятичной системы в двоичную получаем: 0=0, 1=1, а для дальнейшего перевода используют правила сложения. Сложение в двоичной системе основано на том же принципе, что и в десятичной. Чтобы добавить к числу единицу пользуются следующим правилом:
При сложении пишут оба числа одно под другим, как при десятичном сложении. Правила при этом следующие: 0+0=0, 1+0=1, а 1+1=10, при этом в правом разряде пишут 0 и переносят 1 в следующий разряд. Например:
То есть, справа налево получаем:
То есть, получаем 101010.
Вычитание похоже на сложение, только вместо переноса, наоборот, «занимают» единицу из высших разрядов. Умножение тоже похоже на десятичное. Результат перемножения двух единиц — единица, а умножение на ноль дает ноль. Например:
Деление и взятие квадратного корня также мало отличается от работы с десятичными числами.
Классы чисел
Числа объединяются в классы, и некоторые числа могут одновременно входить в несколько классов.
Отрицательные числа
Отрицательные числа обозначают отрицательную величину. Перед ними ставят знак минус, чтобы отличить их от положительных. Например, если человек А должен человеку Б пять рублей, значит у него есть −5 рублей. Здесь –5 — отрицательное число.
Рациональные числа
Рациональные числа — это те числа, которые можно представить в виде дроби, где знаменатель — это положительное натуральное число, а числитель — целое число. Например, 3/4 и −10/5 (то есть, −2) — рациональные числа.
Натуральные числа
Натуральные числа это ноль и положительные целые числа. Например, 7 и 86 766 575 675 456 — натуральные числа.
Целые числа
Целые числа — это ноль, отрицательные и положительные числа, не являющиеся дробями. Например, −65 и 11 223 — целые числа.
Комплексные числа
Комплексные числа получают при сложении действительного (не комплексного) числа и другого действительного числа, умноженного на квадратный корень минус одного. Здесь квадратный корень минус одного называется мнимым числом.
Простые числа
Простые числа — это натуральные числа больше единицы, которые делятся без остатка только на единицу и сами себя. Примеры простых чисел это: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на февраль 2013 г. В нем содержится 17 425 170 цифр. Простые числа используют в криптосистемах с отрытым ключом. Это вид кодирования применяется в шифровании электронной информации в тех случаях, когда необходимо обеспечить информационную безопасность, например, на сайтах интернет-магазинов, электронных кошельков и банков.
Интересные факты о числах
Особая система записи чисел, чтобы предотвратить мошенничество
В Китае используют отдельную форму записи чисел для бизнеса и финансовых операций. Обычные иероглифы, используемые для названий чисел, слишком просты, и их легко подделать или переделать, добавив к ним всего несколько штрихов. Поэтому на банковских чеках и других финансовых документах обычно используют особые более сложные иероглифы.
Современный счет в торговле
В языках стран, где принята десятичная система счисления, до сих пор сохранились слова, свидетельствующие о том, что ранее там использовалась система с другой основой. Например, в английском языке до сих пор используют слово «дюжина», обозначающее двенадцать. Во многих англоязычных странах в дюжинах считают и продают яйца, мучные изделия, вино и цветы. А в кхмерском языке есть слова для счета фруктов, основанные на двадцатеричной системе.
Произношение названий чисел
Арабская система счисления применяется в Китае и Японии, но в отличие от английского, русского, и многих других языков, числа в китайском и японском языках сгруппированы по десять тысяч. То есть, когда в английском или в русском говорят: сто, потом идут кратные сотни, потом тысяча, кратные тысячи, миллион, и так далее, то в японском и китайском языках идут: сто, кратные ста до 9 999, десять тысяч, кратные десяти тысяч до 999 999, 1 000 000, и так далее.
Несчастливые числа
На Западе, а также во многих странах, где исповедуют христианство, 13 считается несчастливым числом. Историки считают, что это связано с христианством и иудаизмом. Согласно Библии, на Тайной Вечере присутствовало именно тринадцать учеников Иисуса, и тринадцатый, Иуда, после предал Христа. У викингов также существовало поверье о том, что когда тринадцать человек собираются вместе, один из них обязательно умрет в следующем году.
В странах, где говорят по-русски, неудачными считаются четные числа. Вероятно, это связано с верованиями древних славян, которые думали, что четные числа — статичны, неподвижны, закончены в одно целое, а значит — мертвые. Нечетные же, наоборот, подвижны, ищут дополнения, изменяются, а значит — живые. Поэтому четное количество цветов приносят только на похороны, но не дарят живым людям.
В Китае, Корее и Японии не любят число 4, потому, что оно созвучно со словом «смерть». Часто избегают не только саму цифру четыре, но и числа, ее содержащие. Например, часто пропускают такие числа в нумерации этажей и квартир. В Китае также не любят число 7, из-за того, что седьмой месяц в китайском календаре — месяц духов. Считается, что в этот месяц граница между мирами людей и духов исчезает, и духи приходят навещать людей. Число 9 считается неудачным в Японии, так как оно созвучно со словом «страдание».
Несчастливое число в Италии — 17, потому что его написание римскими цифрами — «XVII», что можно переписать как «VIXI», изменив порядок букв. Часто эта фраза была написана на могилах древних римлян и означала «я жил», поэтому ассоциируется с концом жизни и со смертью.
666 — известное многим несчастливое число, также именуемое «числом зверя» в Библии. Некоторые считают, что на самом деле «число зверя» — 616, но упоминание о 666 встречается чаще. Многие верят, что этим числом будет обозначен антихрист, наместник дьявола, и иногда ассоциируют это число с самим дьяволом. Так, некоторые убеждены, что 666 и 616 — это зашифрованное имя римского императора Нерона на древнееврейском и латинском языках соответственно, выраженное цифрами. Вероятность действительно существует, так как Нерон известен гонениями христиан и своим кровавым правлением. Некоторые историки даже считают, что именно Нерон являлся инициатором великого пожара Рима, хотя многие историки не согласны с такой трактовкой событий.
В Афганистане, особенно в Кабуле и его окрестностях, распространился слух о том, что число 39 — позорное число, связанное с проституцией. Согласно этому слуху, в Кабуле живет и работает сутенер, чей номерной знак на машине и номер квартиры содержит это число. Некоторые обвиняют правительство и организованные преступные группировки в том, что те специально распустили такой слух, чтобы покупать в Кабуле машины с такими номерными знаками и перепродавать в отдаленных провинциях, до куда не дошел этот слух. Людей с числом 39 в номерном знаке, номере квартиры или телефона дразнят, и насмехаются над ними, и эта проблема настолько серьезна, что многие изменяют цифры на номерных знаках и всячески стараются скрыть причастность к этому числу. Ходят слухи, что ненависть к числу 39 довела до трагедии. Во время выборов в парламент многие насмехались над кандидатом, чей номер в бюллетене был 39. Во время автомобильной пробки ему начали сигналить и кричать, в результате ситуация на дороге ухудшилась и переросла в аварию, и телохранители, опасающиеся за его жизнь, открыли огонь, в результате убив двоих. Парламентарий и его телохранители отрицают причастность к этому происшествию, никого не привлекли к ответственности, и неизвестно, произошло ли событие в действительности, или это только слухи.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
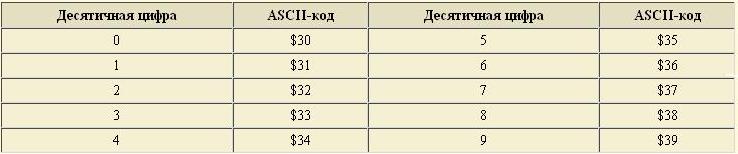
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.