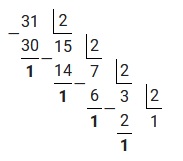перевести шестнадцатеричный код в двоичный
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод из шестнадцатеричной системы счисления в двоичную
Для перевода чисел из шестнадцатеричной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода шестнадцатеричных чисел в двоичную систему счисления
Подробно о переводе из шестнадцатеричной в десятичную систему смотрите на этой странице, о переводе из десятичной в двоичную — здесь. Для целостного понимания, разберем несколько примеров, но для начала вспомним алфавиты двоичной, десятичной и шестнадцатеричной систем счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Перевод целого шестнадцатеричного числа в двоичную систему счисления
Пример 1: перевести число F16 из шестнадцатеричной в двоичную систему.
Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в двоичный код. Решение будет выглядеть следующим образом:
Для перевода шестнадцатеричного числа F16 в десятичную систему, воспользуемся формулой:
F1616=F ∙ 16 2 + 1 ∙ 16 1 + 6 ∙ 16 0 = 15 ∙ 256 + 1 ∙ 16 + 6 ∙ 1 = 3840 + 16 + 6 = 386210
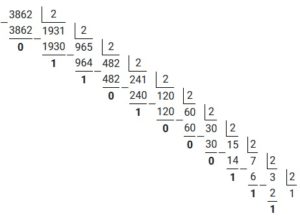
Полученное число 3862 переведем из десятичной системы счисления в двоичную. Для этого, осуществим последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
Полученные остатки записываем в обратном порядке, таким образом:
Перевод дробного шестнадцатеричного числа в двоичную систему счисления
Пример 2: перевести 1F.625 из шестнадцатеричной в двоичную систему счисления.
Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в двоичную:
1. Для перевода числа 1F.625 в десятичную систему воспользуемся формулой:
Обратите внимание! Формула перевода дробного числа в десятичную систему, очень похожа на формулу перевода целого, однако немного отличается.
2. Полученное число 31.384033203125 переведем из десятичной системы счисления в двоичную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
2.1 Для того, чтобы перевести число 31 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.384033203125 в двоичную систему, необходимо выполнить последовательное умножение дроби на 2, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.384033203125 ∙ 2 = 0.76806640625 (0)
0.76806640625 ∙ 2 = 1.5361328125 (1)
0.5361328125 ∙ 2 = 1.072265625 (1)
0.072265625 ∙ 2 = 0.14453125 (0)
0.14453125 ∙ 2 = 0.2890625 (0)
0.2890625 ∙ 2 = 0.578125 (0)
0.578125 ∙ 2 = 1.15625 (1)
0.15625 ∙ 2 = 0.3125 (0)
0.3125 ∙ 2 = 0.625 (0)
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
Ответом станет прямая последовательность целых частей произведения. Т.е.
2.3. Осталось соединить переведенные части, таким образом:
Ответ: 1F.62516 = 11111.011000100102.
Перевод чисел в различные системы счисления с решением
Исходное число записано в -ой системе счисления.
Хочу получить запись числа в -ой системе счисления.
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Конвертер величин
Конвертер чисел в различных системах счисления.
Магнитный поток
Подробнее о числах
Общие сведения
Число — это абстрактное математическое понятие обозначающее количество. Числа используются для счета. Числа использовались человеком с древнейших времен, вначале в виде счетных палочек или зарубок и черточек на дереве и кости, а потом и в виде более абстрактных систем. Существует много способов выражения чисел и работы с ними; некоторые из них приведены ниже. Системы счисления эволюционировали на протяжении многих веков и не все из них используются по сей день.
Различные способы представления чисел
Ученые считают, что понятие числа возникло в разных культурах независимо. Символы для обозначения цифр в письменном виде также возникли в каждой культуре отдельно, но постепенно, с развитием торговли, люди начали обмениваться идеями и заимствовать друг у друга принципы счисления или написания чисел. Поэтому те системы счисления, которыми мы сейчас пользуемся, создавались коллективно многими народами.
Арабские цифры
Арабская система счисления — одна из самых широко используемых систем счисления. Она была заимствована из Индии и доработана персидскими и арабскими математиками. В русском языке эта система называется в основном «арабской», но на других языках, например английском, она чаще называется «индо-арабской». В средние века, особенно ближе к середине и концу этого периода, торговля распространилась по всему миру, и купцы стали привозить в другие страны не только товары, но и сведения о науках, таких как математика. Благодаря этому арабские цифры начали использовать в Европе, сначала в монастырях, а позже и в светском обществе. Папа римский Сильвестр II одним из первых стал использовать и распространять арабские цифры взамен римских, познакомившись с ними благодаря связям с арабскими государствами на территории нынешней Испании. Европейские ученые приспособили и частично изменили написание цифр, и арабская система счисления получила широкое применение не только во всей Европе, но и по всему миру благодаря торговле и во время колонизации других континентов. Арабская система — десятичная, то есть с основанием 10 и с использованием десяти цифр, которыми можно выразить все возможные числа.
Десять — одно из наиболее широко используемых чисел в системах счета, и десятичная система распространена во многих странах. Это связано с тем, что издревле люди пользовались десятью пальцами на руках для счета. До сих пор люди, которые учатся считать или хотят проиллюстрировать пример, связанный со счетом, используют пальцы. Существуют даже такие выражения как «считать на пальцах». В некоторых культурах для счета использовали также и пальцы ног, костяшки пальцев, и даже пространство между пальцами. Интересно, что во многих языках слово, обозначающее пальцы и цифры — одно и то же. Например, в английском, это слово — «digit» (произносится как «диджит»).
Римские цифры
Римские цифры использовались в Древнем Риме и Европе примерно до четырнадцатого столетия. Их до сих пор используют в некоторых контекстах, например на циферблатах часов, в именах Папы Римского, в названиях повторяющихся событий, например, олимпийских игр, и так далее. Римская система счисления использует семь букв латинского алфавита для обозначения всех возможных комбинаций чисел:
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Порядок написания цифр важен потому, что большее число слева от меньшего значит, что оба числа необходимо сложить, в то время как меньшее число слева от большего следует вычесть из большего числа. Например, XI равняется одиннадцати, а IX — это 9. Это правило действует только для чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях эти правила не соблюдаются, и числа пишутся в ряд, например XXXXX.
Системы счисления в других культурах
Во многих культурах использовались системы счисления, похожие на римскую и арабскую. Например, в кириллической системе счисления цифры от одного до девяти, десять, и кратные ста писались буквами кириллицы. Также существовал специальный знак, похожий на тильду «
», который писали над такими цифрами, чтобы показать, что это не буквы. Существовала похожая система и с использованием глаголицы. В еврейской системе счисления буквами еврейского алфавита записывали числа от одного до десяти, кратные десяти, сто, двести, триста, и четыреста. Остальные числа писали как сумму или произведение. Греческая система счисления также похожа на все, приведенные выше.
В некоторых культурах системы счисления были проще. Например, вавилонские цифры можно было записать с помощью двух клинописных знаков, обозначавших единицу (похожего на большую букву «Т») и десять (похожего на букву «С»). Так, например, 32 можно записать как «СССТТ», используя соответствующие знаки. Египетская система счисления похожа, только в ней существовали также символы для нуля, сотни, тысячи, десяти тысяч, ста тысяч и миллиона, а также были специальные знаки для записи дробей. Цифры майя записывались с помощью знаков, обозначавших ноль, единицу и пятерку. Числа выше девятнадцати также имели своеобразное написание. В них использовались знаки для одного и пяти, но с другим расположением, чтобы показать, что значение этих цифр — другое.
Единичная система счисления
В единичной или унарной системе счисления используется только один знак, обозначающий единицу. Каждое число записывается с помощью таких знаков, количество которых равно этому числу. Например, если такой знак — буква «А», то число пять можно записать как «ААААА». Унарная система часто используется учителями, которые учат детей считать, потому что она помогает детям понять зависимость между количеством предметов, например счетных палочек или карандашей, и более абстрактного понятия числа. Часто унарную систему используют во время игр, чтобы записывать очки, набранные командами, или для счета дней или предметов. Причем метод записи в разных культурах отличается. Например, во многих странах, где принят латинский алфавит, чаще используются черточки. Обычно четыре вертикальные черточки перечеркивают горизонтальной или диагональной, и продолжают счет с новой группы черточек. В примере А) на рисунке счет доходит до четырех, эти черточки перечеркивают пятой, дальше добавляют еще пять черточек, и опять начинают новый ряд. Так, счет доходит до двенадцати. В странах, где в языке используют или использовали китайские иероглифы, люди обычно рисуют не четыре черточки, перечеркнутые пятой, а специальный иероглиф из пяти штрихов. Последовательность этих штрихов не произвольная, а установлена правилами правописания. В примере В) на рисунке счет доходит то пяти и человек пишет два первых штриха следующего иероглифа, заканчивая счет на семи. Кроме простого счета и учета, унарную систему также используют в компьютерных технологиях и электронике.
Позиционная система счисления
В позиционной системе счисления значение каждого знака, обозначающего цифру, зависит от его положения в числе. Это значение также зависит от основания системы счисления. Позиция обычно называется разрядом. Например, число 101 в двоичной системе не равно ста одному в десятичной. Рассмотрим позиционную систему на примере десятичной:
Чтобы получить значение числа, складывают все числа, полученные выше, то есть значения чисел в каждом разряде. Такой способ написания чисел позволяет работать с большими числами, и не занимает так много места в тексте, по сравнению с непозиционными системами счисления.
Пример использования позиционирования в десятичной системе: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная система
Двоичная система очень широко используется в математике и вычислительной технике. Все возможные числа представлены в ней с помощью только двух цифр, «0» и «1», хотя в некоторых случаях используют и другие знаки, например «+», «–». При переводе чисел из десятичной системы в двоичную получаем: 0=0, 1=1, а для дальнейшего перевода используют правила сложения. Сложение в двоичной системе основано на том же принципе, что и в десятичной. Чтобы добавить к числу единицу пользуются следующим правилом:
При сложении пишут оба числа одно под другим, как при десятичном сложении. Правила при этом следующие: 0+0=0, 1+0=1, а 1+1=10, при этом в правом разряде пишут 0 и переносят 1 в следующий разряд. Например:
То есть, справа налево получаем:
То есть, получаем 101010.
Вычитание похоже на сложение, только вместо переноса, наоборот, «занимают» единицу из высших разрядов. Умножение тоже похоже на десятичное. Результат перемножения двух единиц — единица, а умножение на ноль дает ноль. Например:
Деление и взятие квадратного корня также мало отличается от работы с десятичными числами.
Классы чисел
Числа объединяются в классы, и некоторые числа могут одновременно входить в несколько классов.
Отрицательные числа
Отрицательные числа обозначают отрицательную величину. Перед ними ставят знак минус, чтобы отличить их от положительных. Например, если человек А должен человеку Б пять рублей, значит у него есть −5 рублей. Здесь –5 — отрицательное число.
Рациональные числа
Рациональные числа — это те числа, которые можно представить в виде дроби, где знаменатель — это положительное натуральное число, а числитель — целое число. Например, 3/4 и −10/5 (то есть, −2) — рациональные числа.
Натуральные числа
Натуральные числа это ноль и положительные целые числа. Например, 7 и 86 766 575 675 456 — натуральные числа.
Целые числа
Целые числа — это ноль, отрицательные и положительные числа, не являющиеся дробями. Например, −65 и 11 223 — целые числа.
Комплексные числа
Комплексные числа получают при сложении действительного (не комплексного) числа и другого действительного числа, умноженного на квадратный корень минус одного. Здесь квадратный корень минус одного называется мнимым числом.
Простые числа
Простые числа — это натуральные числа больше единицы, которые делятся без остатка только на единицу и сами себя. Примеры простых чисел это: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на февраль 2013 г. В нем содержится 17 425 170 цифр. Простые числа используют в криптосистемах с отрытым ключом. Это вид кодирования применяется в шифровании электронной информации в тех случаях, когда необходимо обеспечить информационную безопасность, например, на сайтах интернет-магазинов, электронных кошельков и банков.
Интересные факты о числах
Особая система записи чисел, чтобы предотвратить мошенничество
В Китае используют отдельную форму записи чисел для бизнеса и финансовых операций. Обычные иероглифы, используемые для названий чисел, слишком просты, и их легко подделать или переделать, добавив к ним всего несколько штрихов. Поэтому на банковских чеках и других финансовых документах обычно используют особые более сложные иероглифы.
Современный счет в торговле
В языках стран, где принята десятичная система счисления, до сих пор сохранились слова, свидетельствующие о том, что ранее там использовалась система с другой основой. Например, в английском языке до сих пор используют слово «дюжина», обозначающее двенадцать. Во многих англоязычных странах в дюжинах считают и продают яйца, мучные изделия, вино и цветы. А в кхмерском языке есть слова для счета фруктов, основанные на двадцатеричной системе.
Произношение названий чисел
Арабская система счисления применяется в Китае и Японии, но в отличие от английского, русского, и многих других языков, числа в китайском и японском языках сгруппированы по десять тысяч. То есть, когда в английском или в русском говорят: сто, потом идут кратные сотни, потом тысяча, кратные тысячи, миллион, и так далее, то в японском и китайском языках идут: сто, кратные ста до 9 999, десять тысяч, кратные десяти тысяч до 999 999, 1 000 000, и так далее.
Несчастливые числа
На Западе, а также во многих странах, где исповедуют христианство, 13 считается несчастливым числом. Историки считают, что это связано с христианством и иудаизмом. Согласно Библии, на Тайной Вечере присутствовало именно тринадцать учеников Иисуса, и тринадцатый, Иуда, после предал Христа. У викингов также существовало поверье о том, что когда тринадцать человек собираются вместе, один из них обязательно умрет в следующем году.
В странах, где говорят по-русски, неудачными считаются четные числа. Вероятно, это связано с верованиями древних славян, которые думали, что четные числа — статичны, неподвижны, закончены в одно целое, а значит — мертвые. Нечетные же, наоборот, подвижны, ищут дополнения, изменяются, а значит — живые. Поэтому четное количество цветов приносят только на похороны, но не дарят живым людям.
В Китае, Корее и Японии не любят число 4, потому, что оно созвучно со словом «смерть». Часто избегают не только саму цифру четыре, но и числа, ее содержащие. Например, часто пропускают такие числа в нумерации этажей и квартир. В Китае также не любят число 7, из-за того, что седьмой месяц в китайском календаре — месяц духов. Считается, что в этот месяц граница между мирами людей и духов исчезает, и духи приходят навещать людей. Число 9 считается неудачным в Японии, так как оно созвучно со словом «страдание».
Несчастливое число в Италии — 17, потому что его написание римскими цифрами — «XVII», что можно переписать как «VIXI», изменив порядок букв. Часто эта фраза была написана на могилах древних римлян и означала «я жил», поэтому ассоциируется с концом жизни и со смертью.
666 — известное многим несчастливое число, также именуемое «числом зверя» в Библии. Некоторые считают, что на самом деле «число зверя» — 616, но упоминание о 666 встречается чаще. Многие верят, что этим числом будет обозначен антихрист, наместник дьявола, и иногда ассоциируют это число с самим дьяволом. Так, некоторые убеждены, что 666 и 616 — это зашифрованное имя римского императора Нерона на древнееврейском и латинском языках соответственно, выраженное цифрами. Вероятность действительно существует, так как Нерон известен гонениями христиан и своим кровавым правлением. Некоторые историки даже считают, что именно Нерон являлся инициатором великого пожара Рима, хотя многие историки не согласны с такой трактовкой событий.
В Афганистане, особенно в Кабуле и его окрестностях, распространился слух о том, что число 39 — позорное число, связанное с проституцией. Согласно этому слуху, в Кабуле живет и работает сутенер, чей номерной знак на машине и номер квартиры содержит это число. Некоторые обвиняют правительство и организованные преступные группировки в том, что те специально распустили такой слух, чтобы покупать в Кабуле машины с такими номерными знаками и перепродавать в отдаленных провинциях, до куда не дошел этот слух. Людей с числом 39 в номерном знаке, номере квартиры или телефона дразнят, и насмехаются над ними, и эта проблема настолько серьезна, что многие изменяют цифры на номерных знаках и всячески стараются скрыть причастность к этому числу. Ходят слухи, что ненависть к числу 39 довела до трагедии. Во время выборов в парламент многие насмехались над кандидатом, чей номер в бюллетене был 39. Во время автомобильной пробки ему начали сигналить и кричать, в результате ситуация на дороге ухудшилась и переросла в аварию, и телохранители, опасающиеся за его жизнь, открыли огонь, в результате убив двоих. Парламентарий и его телохранители отрицают причастность к этому происшествию, никого не привлекли к ответственности, и неизвестно, произошло ли событие в действительности, или это только слухи.