перевод бинарного кода в число
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Расшифровка бинарного кода применяется для перевода с машинного языка на обычный. Онлайн инструменты работают быстро, хотя даже вручную это сделать несложно.
Бинарный или двоичный код используется для передачи информации в цифровом виде. Набор из всего лишь двух символов, например 1 и 0, позволяет зашифровать любую информацию, будь то слова, цифры или изображение.

Как шифровать бинарным кодом
Для ручного перевода в двоичный код любых символов используются таблицы, в которых каждому символу присвоен набор нулей и единиц. Наиболее распространенной системой кодировки является ASCII, где применяется 8-ми битная запись, позволяющая читать binary code и делать преобразование текста.
Базовая таблица содержит бинарные коды для латинской азбуки, цифр, некоторых символов.
В расширенную таблицу добавлена интерпретация кириллицы и дополнительных знаков.

Для перевода из двоичного кода в текст или цифры достаточно выбирать нужные набры символов из таблиц. Но, естественно, вручную такую работу выполнять долго. И ошибки, к тому же, неизбежны. Компьютер справляется с расшифровкой куда быстрее. И мы даже не задумываемся, набирая на экране слова, что одновременно производится перевод текста в бинарный код.
Перевод бинарного числа в десятичное
Для ручного перевода числа из бинарной системы счисления в десятичную можно использовать довольно простой алгоритм:
Вот как этот алгоритм выглядит на бумаге:

Онлайн сервисы для расшифровки
Если все же требуется увидеть расшифрованный бинарный код, раскодировать слова, либо, наоборот, перевести их в двоичную форму, проще всего использовать онлайн-сервисы, предназначенные для этих целей.
Удобный инструмент можно найти по этой ссылке:
https://dev20.ru/bin-text
Два окна, привычных для онлайн-переводов позволяют практически одновременно увидеть оба варианта документа в обычной и бинарной форме. Расшифровка осуществляется в обе стороны. Ввод текста на русском или английском языках производится простым копированием и вставкой.
Бинарный код
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 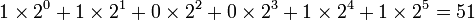
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Бинарный код» в других словарях:
Код Грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея система счисления, в которой два соседних значения… … Википедия
Пойнт-код — Код сигнальной точки (англ. Signal Point Code (SPC)) сигнальной системы 7 (SS7, ОКС 7) это уникальный (в домашней сети) адрес узла, используемый на третьем уровне MTP (маршрутизация) в телекоммуникационных ОКС 7 сетях для идентификации … Википедия
Бесквадратное число — В математике бесквадратным называется число, которое не делится ни на один квадрат, кроме 1. К примеру, 10 бесквадратное, а 18 нет, так как 18 делится на 9 = 32. Начало последовательности бесквадратных чисел таково: 1, 2, 3, 5, 6, 7,… … Википедия
Direct3D 10 — Для улучшения этой статьи желательно?: Викифицировать статью. Переработать оформление в соответствии с правилами написания статей. Исправить статью согласно стилистическим правилам Википедии … Википедия
Python — У этого термина существуют и другие значения, см. Python (значения). Python Класс языка: му … Википедия
Хакерская атака — в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер». Хакерская… … Википедия
Грей — (от англ. gray/grey серый) шотландская и английская фамилия. Содержание 1 Известные носители 2 Грей, как псевдоним известных людей … Википедия
Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия
Крэкерская атака — Хакерская атака в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер» … Википедия
Перевод бинарного кода в число
Побитовые операторы и двоичное представление чисел
Язык программирования С++ обладает полным набором побитовых операторов. Побитовые операторы применяются при выполнении операций с битами в двоичном представлении числовых значений. Прежде чем непосредственно рассмотреть сами операторы, кратко остановимся на концепции двоичного представления числовых значений.
Как известно, целые числа представляются в виде последовательности цифр. Такое представление чисел называется позиционным. Весь набор цифр, которые могут использоваться в позиционном представлении числа, определяют систему счисления. В повседневной жизни используется десятичная система счисления, в которой числа представлены цифрами от 0 до 9.
Каждая позиция в двоичном представлении числа соответствует биту. Таким образом, с помощью бита можно записать два значения: 0 или 1. Если для представления числа используется n бит, то в этом случае существует 2 n различных комбинаций, каждая из которых соответствует отдельному числу. Например, с помощью 8 бит(1 байт) можно записать 2 8 = 256 чисел.
С отрицательными числами дела обстоят несколько сложнее. Чтобы перевести отрицательное число с позиционным представлением в двоичной системе bnbn-1. b2b1b0 (старший бит для отрицательного числа bn = 1), необходимо проделать несложную процедуру из двух этапов.
Во-первых, производится побитовое инвертирование кода, т.е. каждый бит в представлении числа меняется на противоположный: 0 на 1 и 1 на 0.
Чтобы перевести число из десятичной системы в двоичную, проделывают обратную процедуру: от модуля отрицательного числа отнимается 1, результат переводится в бинарный код, после чего проводится побитовое инвертирование.
Проиллюстрируем это не примере.
Рассмотрим 8-битовое бинарное положительное число 01001011, что в десятичной системе счисления соответствует числу 2 0 + 2 1 + 2 3 + 2 6 = 1 + 2 + 8 + 64 = 75.
В том, что это так, легко убедиться: сложим числа 01001010 и 10110101. Формально получаем 100000000, однако поскольку числа 8-битовые, лишний единичный старший бит отбрасывается, и получается представление 00000000, что соответствует нулю, как и должно быть.
Теперь рассмотрим основные побитовые операции и операторы, которые используются для этого в языке программирования С++. Список побитовых операторов приведен в таблице 1.6.







