перевод числа в бинарный код
Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
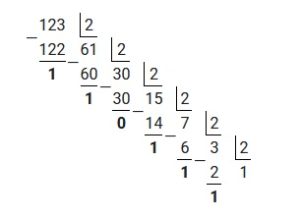
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
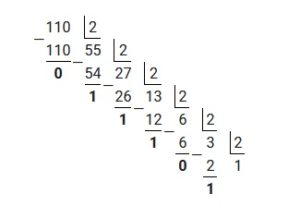
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления






Способы представления чисел
Алгоритм перевода чисел из одной системы счисления в другую
Для перевода числа из двоичной системы счисления в восьмиричную (шестнадцатиричную) необходимо от запятой вправо и влево разбить двоичное число на группы по три (четыре – для шестнадцатиричной) разряда, дополняя при необходимости нулями крайние группы. Каждую группу заменяют соответствующей восьмиричной или шестнадцатиричной цифрой.
Таблица для перевода в восьмеричную систему счисления
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 144
100 = 1448
Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.12*8 = 0.96 (целая часть 0 )
0.96*8 = 7.68 (целая часть 7 )
0.68*8 = 5.44 (целая часть 5 )
0.44*8 = 3.52 (целая часть 3 )
Получаем число в 8-ой системе счисления: 0753.
0.12 = 0.7538
2 Этап. Перевод числа из десятичной системы счисления в восьмеричную систему счисления.
Обратный перевод из восьмеричной системы счислений в десятичную.
Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
144 = 8 2 *1 + 8 1 *4 + 8 0 *4 = 64 + 32 + 4 = 100
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод числа в бинарный код
Двоичные числа представляют числа в двоичной записи.
В двоичном формате число представлено как «01» с 2 в качестве основания.
Пример преобразования в двоичную форму выглядит следующим образом. Для справки также предоставляется пример преобразования восьмеричных и шестнадцатеричных чисел.
| Десятичное | Двоичные | Восьмеричные | Десятичные |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| Десятичное | Двоичные | Восьмеричные | Десятичные |
|---|---|---|---|
| 0.5 | 0.1 | 0.4 | 0.8 |
| 0.75 | 0.11 | 0.6 | 0.C |
| 0.9 | 0.11100110011001. | 0.71463. | 0.E666. |
Анализ доступа
Этот сайт использует службу анализа доступа (Google Analytics).
Эти службы анализа доступа используют файлы cookie для сбора данных о трафике.
Для получения дополнительной информации, пожалуйста, нажмите ЗДЕСЬ.
Реклама
Этот сайт использует рекламную службу (Google AdSense) для размещения на сайте рекламы, распространяемой третьими сторонами.
Эти рекламные службы используют файлы cookie для показа рекламы продуктов и услуг, которые вас интересуют.
Для получения дополнительной информации, пожалуйста, нажмите ЗДЕСЬ.
Перевод чисел в различные системы счисления с решением
Исходное число записано в -ой системе счисления.
Хочу получить запись числа в -ой системе счисления.
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.