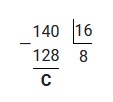перевод двоичного кода в шестнадцатиричный
Перевод из двоичной системы счисления в шестнадцатеричной
Для перевода чисел из двоичной системы в шестнадцатеричную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода двоичных чисел в шестнадцатеричную систему счисления
Подробно о переводе из двоичной в десятичную систему смотрите на этой странице, о переводе из десятичной в шестнадцатеричную — на смотрите здесь. Для целостного понимания, разберем несколько примеров, но для начала вспомним алфавиты двоичной, десятичной и шестнадцатеричной систем счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Перевод целого двоичного числа в шестнадцатеричную систему счисления
Пример 1: перевести 1011101 из двоичной системы в шестнадцатеричную.
Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в шестнадцатеричную. Решение будет выглядеть следующим образом:
Для перевода двоичного числа 1011101 в десятичную систему, воспользуемся формулой:
10111012=1 ∙ 2 6 + 0 ∙ 2 5 + 1 ∙ 2 4 + 1 ∙ 2 3 + 1 ∙ 2 2 + 0 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310
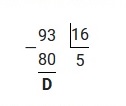
Полученное число 93 переведем из десятичной системы счисления в шестнадцатеричную. Для этого, осуществим последовательное деление на 16, до тех пор пока остаток не будет меньше чем 16.
Полученные остатки записываем в обратном порядке, таким образом:
Перевод дробного двоичного числа в шестнадцатеричную систему счисления
Пример 2: перевести 10001100.110 из двоичной в шестнадцатеричную систему счисления.
Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в шестнадцатеричную:
1. Для перевода числа 10001100.110 в десятичную систему воспользуемся формулой:
Обратите внимание! Формула перевода дробного числа в десятичную систему, очень похожа на формулу перевода целого, однако немного отличается.
2. Полученное число 140.75 переведем из десятичной системы счисления в шестнадцатеричную. Для этого потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
2.1 Для того, чтобы перевести число 140 из десятичной системы счисления в шестнадцатеричную, необходимо осуществить последовательное деление на 16, до тех пор пока остаток не будет меньше 16-ти.
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.75 в шестнадцатеричную систему, необходимо выполнить последовательное умножение дроби на 16, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
Т.к. дробная часть 0, продолжать умножение не нужно. Ответом станет 0.12 (0.С). Т.е.
2.3. Осталось соединить переведенные части, таким образом:
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод чисел в различные системы счисления с решением
Исходное число записано в -ой системе счисления.
Хочу получить запись числа в -ой системе счисления.
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Шестнадцатеричный код.
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Применение. Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код, можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи. В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 303210, в шестнадцатеричной системе данное число будет иметь запись BD816.
В синтаксисе языков программирования. Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код:
* В C, C++ и схожих языках (Java) для этого используется префикс «0x», например: 0x0A0B;
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Общие сведения
Система счисления — метод символьного типа для записи чисел с помощью определенных знаков. Последние записываются посредством чисел и цифр. Однако не все понимают логического смысла последних терминов. Числом называется некоторая абстрактное значение, характеризующее количественные характеристики какой-либо величины, явления или процесса. Цифра является знаком, который необходим для записи числа.
Цифры бывают 2 видов: арабскими и римскими. Первые являются самыми распространенными. Они представлены знаковым интервалом от 0 до 9. Чисел больше, и поэтому используется набор цифр. Для этого и были придуманы системы исчисления. Они делятся на четыре группы:
К первой группе относятся все разрядные системы, в которых положение и порядок знака играет важную роль. От этого зависит значение величины. Если изменить положение цифр, то число изменится.
Смешанной является система, в которой присутствуют данные позиционной и непозиционной групп.Простой пример — деньги. Существуют два типа денежных знаков: монеты и купюры. Например, техника стоит 5250 рублей 50 копеек.
Для получения данной суммы следует использовать некоторое количество купюр и монет: 5250,50 = (5000 + 200 + 50) рублей + 50 копеек.
Унарной называется единичная система с одной цифрой. Последняя может быть представлена в виде 1, черты, креста и любого целого значения. Иными словами, каждый знак соответствует 1. Например, запись «1111111» эквивалентна «|||||||». Если расшифровать ее, то получится число 7. В книге Даниэля Дефо «Робинзон Крузо» герой применял данную систему для подсчета дней, проведенных на острове. Детей обучают математике на начальном уровне с помощью счетных палочек. Если вспомнить историю, то древние люди тоже пользовались унарным счислением.
Позиционные системы в программировании
Наиболее востребованными в IT-сфере являются двоичный и шестнадцатеричный коды. Они применяются для перевода десятичной системы счисления, которая понятна человеку, в машинный язык. Двоичная состоит из двух переменных, которые принимают единичное (1) или нулевое (0) значения. Это очень просто реализовать в электронике и микросхемотехнике.
Микропроцессор персонального компьютера является микросхемой. Она состоит из множества транзисторов, способных кодировать 0 и 1. Схему соединения полупроводниковых приборов составляют так, чтобы они имели два состояния (открыт и закрыт). Кроме того, реализация двоичной системы может быть выполнена в любом устройстве, которое потребляет электрический ток. Наличие кодируется как 1, а отсутствие — 0.
Берутся также некоторые физические процессы: наличие света, сопротивления, намагниченности и так далее. С системой можно связать разные величины, которые имеют два состояния. Новичкам рекомендуется сначала полностью освоить перевод из десятичной системы счисления в двоичную и обратно. После этого следует приступить к изучению шестнадцатеричного кода, расшифровка которого существенно отличается.
Работа с двоичным кодом
Выполнять манипуляции с двоичным кодом достаточно просто. Для этого следует знать основные правила и методы конвертации десятичной системы в двоичную.
Для преобразования IT-специалисты предлагают 3 метода:
Первый и второй способы используются на первоначальных этапах знакомства с системами. Они считаются ресурсоемкими, поскольку отнимают время. Последний реализуется с помощью специальных программ, поддерживающих конвертацию из одной системы в другую. Этим методом пользуются все программисты. В различных операционных системах есть приложения, работающие в таком режиме (например, калькулятор Windows).
Однако нужно подробнее разобрать первые два метода, поскольку задачи на конвертацию могут быть на экзаменах или контрольных.
Деление с отсечением остатка
Начинающему программисту необходимо обязательно знать алгоритм преобразования, и уметь применять его на практике. К
роме того, на экзаменах по дисциплинам с IT-уклоном может быть задача, в которой следует выполнить конвертацию из одной системы счисления в другую.
Перевод числа из десятичной в двоичную осуществляется по такому алгоритму:
Для наглядного примера стоит применить алгоритм на практике.
Для перевода числа 13 нужно выполнить следующие шаги:
Нужно обратить внимание на форму записи в 6 пункте.
Таким способом правильно записывается число в системах счисления.
Можно применять также вместо <2>нижний индекс, указывающий искомую систему.
Последний пункт нужно выполнять постоянно, поскольку это поможет избежать проблем при расчетах.
Если ничего нет под рукой, то можно произвести возведение в степень. Это делается следующим образом: [1011] <2>= 2 3 + 0 + 2 1 + 2 0 = 8 + 0 + 2 + 1 = [13]<10>.
Степенной метод
Для реализации этого метода необходимо воспользоваться таблицей степеней двойки (табл. 1). Ее можно составить самостоятельно или скачать из интернета. Суть метода сводится также к вычислениям и подборам значений.
| Показатель степени, n | Результат возведения |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
Таблица 1. Степень двойки до 6 и ее значения.
Специалисты рекомендуют воспользоваться обыкновенным калькулятором, который разрешен на экзаменах или тестах. Кроме того, следует составить таблицу, поскольку это оптимизирует процесс вычислений. Для конвертации есть специальный алгоритм:
Для проверки рекомендуется воспользоваться специальным калькулятором или выполнить сложение всех значений степеней. Для примера можно рассмотреть конвертацию числа 118 в двоичный код. Операция выполняется таким образом:
Чтобы проверить в ручном режиме, нужно произвести обратные вычисления: 2 6 + 2 5 + 2 4 + 0 + 2 2 + 2 1 + 0 = [118]<10>.
Шестнадцатеричный формат
Осуществить конвертацию из десятичного в шестнадцатеричный код (HEX — hexadecimal) можно только с использованием программ. Ручной метод основан на двойной конвертации. Для его реализации нужно перевести число, записанное в десятичной системе, в двоичный код, а затем в шестнадцатеричный.
Основанием является целочисленное значение, равное 16. Система состоит из арабских цифр от 0 до 9, а также букв, обозначающих конкретные значения: А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15. В автоматизированном режиме можно воспользоваться переводчиком шестнадцатеричного кода.
Необходимо отметить, что HEX применяется также в низкоуровневом программировании. Выбор этой системы счисления основан на решении в компьютерной технике применять такую единицу информации, как байт (состоит из 8 битов). Его удобно записывать двумя HEX-цифрами (от 0 до 255, т. е. #00 до #FF). Кроме того, шестнадцатеричный код в текст также конвертируется. Примером этому является кодировка Юникод, в которой для записи символа применяются четыре HEX-цифры. Цвет RGB-формата графического изображения также записывается с его помощью.
Способы записи
Существует несколько форм записи числа, представленного в HEX. Математическая форма выглядит таким образом: [DF5]<16>. Можно также найти запись, в которой вместо <16>стоит нижний индекс. Она применяется в информатике.
Запись отличается в языках программирования, поскольку у каждого из них различный синтаксис и правила написания кода. Основные формы представления HEX следующие:
Распространенная ошибка новичков заключается в том, что они неверно указывают HEX-числа. В результате компилятор языка выдает ошибку. Программисты рекомендуют основательно изучить синтаксис языка перед написанием приложений.
Алгоритм конвертации
Перевод в шестнадцатеричный код рекомендуется осуществлять с помощью специальных приложений (конвертеров кода). Если же их нет под рукой, то специалисты рекомендуют использовать специальный алгоритм:
Операции умножения, сложения, вычитания и деления сложны.
Они осуществляются только с помощью специальных программ или онлайн-сервисов.
Не следует путать четверичные с троичными группами, которые используются в восьмеричном коде.
Например, нужно перевести 118 в HEX-код.
Для этого следует воспользоваться описанным алгоритмом:
В некоторых случаях нужно использовать буквы. Например, для перевода числа [11110111] <2>в HEX-код нужно также воспользоваться алгоритмом, разбивая его на тетрады следующим образом: 1111 0111. Первая группа равна 2 3 + 2 2 + 2 1 + 2 0 = [15] <10>= F<16>, а вторая — 0 + 2 2 + 2 1 + 2 0 = 7. Результирующая запись имеет такой вид: [11110111] <2>= [F7]<16>.
Таким образом, HEX-код получил широкое применение в IT-сфере, поскольку он очень удобен для записи массивов информации. Однако для его конвертации в ручном режиме нужно изучить двоичную систему счисления, а также основные алгоритмы преобразования.