перевод в доп код
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Дополнительный код (представление числа)
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2). [2]
Содержание
Представление числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения, которое противоположно по знаку, все разряды, включая знаковый, инвертируются, а затем к результату добавляется единица.
| Десятичное представление | Код двоичного представления (8 бит) | |
|---|---|---|
| прямой | дополнительный | |
| 127 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 |
| -0 | 10000000 | ——— |
| -1 | 10000001 | 11111111 |
| -2 | 10000010 | 11111110 |
| -3 | 10000011 | 11111101 |
| -4 | 10000100 | 11111100 |
| -5 | 10000101 | 11111011 |
| -6 | 10000110 | 11111010 |
| -7 | 10000111 | 11111001 |
| -8 | 10001000 | 11111000 |
| -9 | 10001001 | 11110111 |
| -10 | 10001010 | 11110110 |
| -11 | 10001011 | 11110101 |
| -127 | 11111111 | 10000001 |
| -128 | ——— | 10000000 |
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| . | . |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| . | . |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| . | . |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| . | . |
Преобразование дополнительного кода
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1
Допишем слева знаковый единичный разряд
Для обратного преобразования используется тот же алгоритм. А именно:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1 и проверим, сложив с дополнительным кодом
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
Представление чисел в ЭВМ
Целые числа
Для числа +1101 :
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
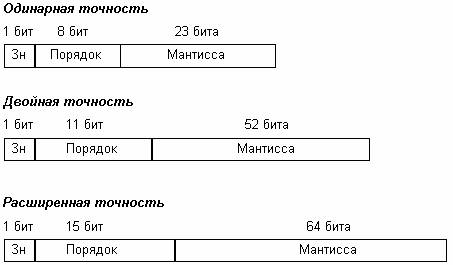
Вещественные числа (числа с плавающей точкой)
0.15625 = 001012
446.15625 = 110111110,001012 = 1,1011111000101*2 8
Знак S = 0
Порядок P = 8 + 1023 = 103110 = 100000001112
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE2800000000016
455,375 = 111000111,01102 = 1,110001110110*2 8 2
Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 100000010002 = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101
1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881
б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 100000010002 = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011
1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818
Перевести число в прямой, обратный и дополнительный код
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Перевести число из десятичной системы в прямой, обратный и дополнительный код Delphi 7
добрый вечер, всем участникам прекрасного форума. помогите, пожалуйста, написать программу на.
Перевести X и Y в прямой, обратный и дополнительный коды
Перевести X и Y в прямой, обратный и дополнительный коды. Сложить их в обратном и дополнительном.
Прямой обратный дополнительный код
procedure programma; var i,pp,kod,chislo,op,po:integer; c,a,b:string; rez :array of integer;.
прямой дополнительный и обратный код
как в прямом и обратном коде считать я разобрался, а как считать в дополнительном? я уже второй.
Fizzy, Начать нужно с того, что, когда Вы копируете сюда код своей программы, используйте в окне кнопку Python (‘Выделить код Python’) и туда, между тегами, вставляйте свою программу, что бы не пропадали отступы из Вашей программы. Тогда будет проще отвечать на Ваш вопрос, учитывая, что ошибка у Вас может быть и в неправильных отступах. Отступы являются частью синтаксиса Python.
Добавлено через 23 минуты
Fizzy, Когда Вы работаете с дополнительным кодом, он будет выглядеть по разному для компьютеров разной разрядности 4, 8, 16, 32. Хотя вычисления будут одинаковыми. Поэтому укажите для какой разрядности Вы хотите получить дополнительный код.
https://ru.qaz.wiki/wiki/Two%27s_complement
Я в свое время как то разобрался с дополнениями, но сейчас подзабыл. Если сами не разберетесь и никто не подскажет, то позже освежу у себя в памяти и попробую помочь.
Добавлено через 8 минут
Для понимания инверсии
можете еще посмотреть
«»»https://f o o o b a r.com/questions/13665/bit-wise-operation-unary-invert»»»
Взял в кавычки, так как иначе ссылка не выводится
И уберите пробелы в f o o o b a r.com
Добавлено через 1 час 26 минут
Более простым языком
«»»https://o t v e t.mail.ru/question/39094525″»»
Слитно o t v e t.mail.ru
Добавлено через 1 час 1 минуту
Добавлено через 12 минут
Цитата из последней ссылки:
«Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления, но формат представления чисел в прямом коде неудобен для использования в вычислениях, поскольку сложение и вычитание положительных и отрицательных чисел выполняется по–разному, а потому требуется анализировать знаковые разряды операндов. Поэтому прямой код практически не применяется при реализации в АЛУ арифметических операций над целыми числами. Вместо этого формата широкое распространение получили форматы представления чисел в обратном и дополнительном кодах.»