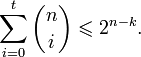питерсон уэлдон коды исправляющие ошибки
Питерсон У., Уэлдон Э. Коды, исправляющие ошибки (1976), страница 2
Описание файла
Просмотр DJVU-файла онлайн
Необходимость пересмотра первого издания возникла по меньшей мере пять лет назад. Однако с момента опубликования первого издания было напечатано так много новых работ по теории кодов, исправляющих ошибки, что подготовка второго издания оказалась практически значительно более трудной задачей, чем написание оригинальной монографии. Уже при работе над первой книгой много раз приходилось решать вопрос о целесообразности включения того или иного материала. Принятие подобных решений для второго издания оказалось еще более трудным и субъективным, и мы сознаем, что во многих случаях эти решения спорны.
Без сомнения, наиболее серьезным пробелом данной монографии является отсутствие обзора последних работ, выполненных в Советском Союзе и странах Восточной Европы. Основные из этих работ включены в книгу В. Д. Колесника и Е. Т. Мирончикова «Декодирование циклических кодов» (1968), заслуживающую самой высокой оценки, Значительная часть этой книги посвящена мажоритарному декодированию. В превосходной книге С.
И. Самойленко «Помехоустойчивое кодирование» (1966) особое внимание уделяется кодам, исправление ошибок в которых легко осуществляется посредством вычислительных машин. Известны также монографии 1О. Г. Дадаева «Арифметические коды, исправляющие ошибки» (1969) и Л. Ф.
Бородина «Введение в теорию помехоУстойчивого кодирования» (1968). В последней описываются некоторые методы декодирования, основанные на использовании аналоговых сигналов на выходе. Показателем размаха работ в СССР по этим вопросам является также обширная библиография «Обзор новых результатов по теории кодирования в Советском Союзе»,составленная Каутцем и Левиттом (1ЕЕЕ Тгапз., 1Т-15, № 1, Р1.
11), которой упоминается свыше четырехсот работ по теории кодирования. В связи с этим, быть может, самым подходящим для данной книги явилось бы название «Коды, исправляющие ошибки, в Западном мире». Второе издание по существу содержит весь материал первого издания. Наиболее значительные добавления — гл. 10, в которой описываются мажоритарные коды, гл. 12 о синхронизации и гл. 13 и 14, посвященные сверточным кодам. Много нового материала включено в гл. 5 и 8. Мы рады возможности поблагодарить коллегу по Гавайскому университету Шу Линя за многие полезные замечания и обсуждение, продолжавшееся в течение четырех лет, которые понадобились для написания этой книги.
Значительный вклад в данную работу сделали также Касами, Чен и Берлекэмп. Отдельные главы в книге связаны следующим образом: 1, 2, 3(1, 2), 4(3), 5(3), 6(2), 7(6), 8(3, 7), 9(8), 10(8), 11(8), 12(8), 13(3), 14(3), 15(6). У. Питерсов, И. Дк. Увиден мл. 1 Проблема кодирования В течение последних двух десятилетий несколько важных до. стижений стимулировали быстрое развитие кодов, исправляющих ошибки, То внешнее для теории кодирования обстоятельство, что стоимость электронных устройств на интегральных схемах в последние годы убывала почти со столь же драматической скоростью, как и их размеры, ускорило развитие цифровой вычислительной техники и периферийных устройств вычислительных машин, что а свою очередь привело к драматическому росту количества данных, передаваемых от одной машины к другой.
Недопустимость ошибок а вычислительных системах, а в некоторых случаях и критическая природа самих данных требовали использования оборудования, исключающего ошибки, или какого-либо рода кодов, исправляющих или обнаруживающих ошибки на выходе конечных устройств. Во многих случаях более выгодным оказывается второй путь. С другой стороны, значительные успехи были достигнуты н в самой области кодов, исправляющих ошибки.
Создано несколько классов длинных мощных кодов. Кроме того, для некоторых из этих классов кодов разработаны процедуры декодирования, которые не требуют большого количества оборудования. Эти и другие достижения привели к тому, что в настоящее время использование кодов, исправляющих ошибки, стало действительно практически осуществимым в системах для передачи данных.
Естественный прогноз состоит в том, что в ближайшем будущем указанные выше тенденции будут продолжать развиваться, и коды, исправляющие ошибки, будут находить все более широкое применение. В этой главе вводится понятие канала связи„ описывается роль кодов при передаче информации, определяются блоковые и древовидные коды и другие важнейшие понятия. 1. Канал связи Принципиальная схема цифровой системы связи изображена на фиг.
1.1. Эта же самая модель описывает и систему хранения информации, если среду, в которой хранится информация, рассматр ать как канал. Типичным каналом для передачи информации ривать к валяется телефонный канал. для хранения информации обычно использ е ьзуется магнитофон, имеющий записывающую н считывающую ланпл или арейа, а ллщнрай ираишпсн трлрмпция Кодар лалрчащаль Фиг.
1.1, Блок-схема общей системы передачи нли хранении информации, головки. Источником информации является, как правило, сообщение, состоящее из двоичных или десятичных цифр, или же текст, записанный с помощью некоторого алфавита. Кодер преобразует эти сообщения в сигналы, которые могут быть переданы по каналу. Типичными сигналами явля1отся электрические сигналы с некоторыми ограничениями по мощности, полосе частот и продолжительности.
Эти сигналы поступают в канал и искажаются шумом. Затем искаженный сигнал поступает в декодер, который восстанавливает посланное сообщение и направляет его получателю. Основная задача, возникающая в технике связи, состоит в том, чтобы построить кодер и декодер, хотя она может включать в себя также задачу улучшения самого канала. Заметим, что кодер включает в себя устройство, которое обычно называют модулятором, а в декодер входит устройство, которое обычно называют детектором. Анализ показывает, что в большинстве случаев каналы связи, описываемые схемой, представленной на фиг.
1.1, обладают определенной пропускной способностью для передачи информации. Более того, если скорость создания информации источником сообщения меньше пропускной способности канала, то можно выбрать совокупность сигналов так, чтобы вероятность ошибочного декодирования была произвольно малой 179, 81, 173, 270. 273$ Теория не указывает точно, как следует выбирать эти сигналы, но гарантирует реальное су1цествование соответствующей системы передачи. Использование кодов, исправляющих ошибки, является попыткой разрешить одновременно обе проблемы.
Система, в которой используются типы кодирования, рассматриваемые в этой книге, изображена на фиг. 1.2. Преобразователи в этой системе просто переводят символы одного алфавита в символы другого алфавита. Обычно оба алфавита невелики — типичным преобразованием является переход от десятичного алфавита к двоичному. На вход модулятора подается один символ, который превращается на его выходе в сигнал соответствуюшеи формы, т.
Независимое демодулирование отдельных импульсов приводит к дальнейшему уменьшению пропускной способности канала. Кодер и декодер реализуют используемый код, исправляющий ошибки. Эффективное построение этих устройств и является предметом этой книги. Даже если разделение приемника на демодулятор и декодер, а передатчика на модулятор и кодер приводит к уменьшению предельных возможностей данной системы передачи, тем не менее все же можно добиться произвольно малой вероятности ошибочного декодирования, хотя и прн несколько меньшей пропускной способности канала. Кроме того, что даже важнее с практической точки зрения, использование кодирования дает возможность спроектировать и построить высокоэффективные системы передачи и хранения информации.
Блок-схема типичной системы связи с яспольвопаппем копов, исправляющих ошябкя. и, быть может, исправлять такие ошибки. Эти коды не могут исправлять любую возможную комбинацию ошибок; они скорее предназначаются для того, чтобы исправлять наиболее правдоподобные комбинации ошибок. Ббльшая часть теории двоичных кодов основана на предположении, что каждый из символов искажается шумом независимо и что, следовательно, вероятность данной комбинации ошибок зависит только от числа ошибок. Так, например, разработаны коды, которые исправляют любую комбинацию из 1 или меньшего числа одиночных ошибок в блоке из п символов.
Питерсон У., Уэлдон Э. Коды, исправляющие ошибки (1976), страница 59
Описание файла
Просмотр DJVU-файла онлайн
Наилучший двоичный (12,4)-код имеет минимальное расстояние 6. (См. табл. 5.4.) Существует квазициклнческий код с теми же параметрами; порождающая матрица этого кода имеет вид 111 011 000 00! 001 111 О!1 000 000 001 111 011 011 000 001 111 Кодирование для этого кода можно производить с помощью регистра сдвига с й = 4 ячейками, изображенного на фиг. 8.8. Этот регистр работает следующим образом: после ввода четырех информационных символов в регистр ключ 2 закрывается, ключ 1 открывается, а выходы двух двоичных сумматоров равны двум проверочным символам в первом блоке из трех символов кодового слова.
Символы этого блока затем поступают в канал в обычном порядке: сначала информационные, а потом проверочные. Затем происходит один сдвиг регистра, и процесс повторяется. В силу свойства квазицикличности следующие два проверочных символа снова появятся па выходах сумматоров. Кодирование заканчивается, когда последний информационный символ будет считаи в данном случае после четырех сдвигов.
ных кодов, исправляющих случайные ошибки. В табл. 8.3 пере- Таблица 8.3. Некоторые двоичные клазициклические (л, л/2)-коды. Каждый из неречисленных кодов обладает наибольшим значением л среди кзазициклическнх кодов той же длины цри ге=0,5 Порождающаи строк» циркулиита(а восьмеричном иредстаалелниг Минимальное расстои- ние Л длина л числены квазициклическне 1п,п12)-коды при различных значениях и, обладающие наибольшим минимальным расстоянием среди квазициклнческих кодов 1421 Кроме значений и н е1, в восьмеричной форме приводится верхняя строка цнркулянтной матрицы, которая полностью определяет матрицу чи.
Заслуживает внимания тот факт, что во всех исследованных до сих пор случаях на этих кодах, обеспечивающих скорость передачи, равную ‘гт„достигается наибольшее известное значение минимального расстояния в классе всех линейных кодов с теми же самыми значениями и и /г.
В свете этого последнего замечания было бы желательно привести здесь методы построения квазицнклических кодов; к сожалению, только один метод построения квазициклическнх кодов был известен автору. Хотя эти самоортогональные квазнциклические коды
3051 могут быть декодированы посредством очень простого мажоритарного декодера, они обладают относительно малым минимальным расстоянием. Доказано существование очень длинных, хотя и не сколь угодно длинных, двоичных квазициклических кодов, для которых достигается граница Гилберта [441 Для этих кодов, обладающих невы- рожденными циркулянтными матрицами, достигается также гра- 6 1О 12 14 16 18 20 22 24 26 28 30 ’32 34 36 38 40 42 3 7 7 7 7 27 117 57 267 573 653 727 2!67 557 557 573 557 5 723 14 673 3 4 4 4 4 5 6 6 7 8 7 8 8 8 8 8 8 9 10 ница вероятности ошибки случайного кодирования с вычеркиваниями.
(т изоморфна алгебре мпогочленов по модулю Х
(8.55) Таким образом, кодовое слово квазициклического кода можно рассматривать как информационный многочлен, за которым следует кодовое слово циклического кода длины А, порожденного наибольшим обшим делителем многочленов с(Х) и Х» — 1. Некоторые циклические коды близко связаны с квазициклическими кодами. Рассмотрим, например, квадратичпо-вычетный (17,9)-код, минимальное расстояние которого равно 5. Пусть а— корень многочлепа Ха+ Х’+ Ха+ Х+ 1.
Положим р = а’з. Тогда ч(Х) = т(р) = Ха+ Хт+Хз+ Ха+ Ха+ Х+ 1. Проверочная матрица этого кода может быть записана в виде 1! (р
Можно доказать, что 5′ = ат + сФ. Тогда сопряженные элементы для рз являются циклическими сдвигами набора длины 8: 00! 00001. 27 Можно показать, что корень рв представляется в виде а’ +а’ + +а
т. д. Эту теорему используем для построения класса кодов, исправляющих случайные ошибки, над полем ОР(д ). Выберем в ка- /П т
Коды, исправляющие ошибки
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Содержание
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 
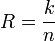
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 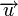

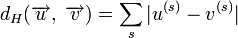
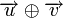
Минимальное расстояние Хемминга 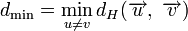
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром

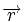
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 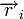

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 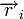
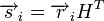
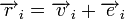
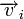
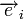

Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 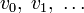
Порождающий (генераторный) полином
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Таким образом, вид полинома g(x) задаёт конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | x 12 + x 11 + x 3 + x 2 + x + 1 |
| CRC-16 | 16 | x 16 + x 15 + x 2 + 1 |
| CRC-x 16 + x 12 + x 5 + 1 | ||
| CRC-32 | 32 | x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 |
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома g(x) на множители в поле Галуа.
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
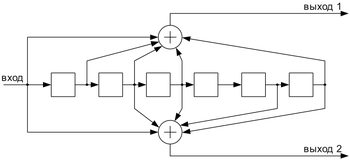
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Коды, исправляющие ошибки» в других словарях:
Коды исправляющие ошибки — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Исправляющие ошибки Коды — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Коды Рида-Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код Рида Соломона является … Википедия
КОРРЕКТИРУЮЩИЕ КОДЫ — коды, обнаруживающие и исправляющие ошибки при передаче и обработке информации в линиях связи или сложных информац. системах. В основе корректирования лежит использование избыточности сообщений, при к рой часть символов кодового слова можно… … Большой энциклопедический политехнический словарь
Корректирующие коды — помехоустойчивые коды, коды обнаружения и исправления ошибки, Коды, позволяющие по имеющейся в кодовой комбинации избыточности (См. Избыточность) обнаруживать и исправлять определённые ошибки, появление которых приводит к образованию… … Большая советская энциклопедия
Код Рида — Коды Рида Соломона (англ. Reed–Solomon codes) недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона,… … Википедия
Код коррекции ошибок Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
Код Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
РС код — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
Код Боуза — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия