Числовая система ЭВМ. Представление целых чисел без знака и со знаком

Введем основные понятия на примере 4-битовых машинных слов. Такой размер слова обеспечивает хранение десятичных чисел только от 0 до 15 и поэтому не представляет практического значения. Однако они менее громоздки, а основные закономерности, обна­руженные на примере 4-битовых слов, сохраняют силу для машин­ного слова любого размера.

Предположим, что процессор ЭВМ способен увеличивать (прибавлять 1) и дополнять (инвертировать) 4-битовые слова. Например, результатом увеличения слова 1100 является 1101, а ре­зультатом дополнения этого слова является ООН. Рассмотрим слово 0000, представляющее десятичное число 0. В результате увеличения содержимое этого слова станет равным 0001, что соответствует десятичному числу 1. Продолжая последовательно увеличивать 4-битовые слова, придем к ситуации, когда, увеличивая слово 1111 (которое представляет десятичное число 15), получим в результате слово 0000, т. е. 111+1 = 0000 (15+1=0), при этом получили неверную арифметическую операцию и вернулись в исходное состояние. произошло из-за того, что слово памяти может состоять только конечного числа битов. Таким образом, числовая система ЭВМ является конечной и цикличной.

Если знаковый бит равен нулю, то значение числа легко вычисляется — игнорируется знаковый бит, а оставшиеся три бита интерпретируются как двоичный код десятичного числа. Например, слово 0110 представляет двоичное число 110, которое равно десятич­ному числу 6.

Проведение независимой экспертизы проектной документации на сайте

Источник

Числовая система ЭВМ. Представление целых чисел без знака и со знаком

Введем основные понятия на примере 4-битовых машинных слов. Такой размер слова обеспечивает хранение десятичных чисел только от 0 до 15 и поэтому не представляет практического значения. Однако они менее громоздки, а основные закономерности, обна­руженные на примере 4-битовых слов, сохраняют силу для машин­ного слова любого размера.

Предположим, что процессор ЭВМ способен увеличивать (прибавлять 1) и дополнять (инвертировать) 4-битовые слова. Например, результатом увеличения слова 1100 является 1101, а ре­зультатом дополнения этого слова является ООН. Рассмотрим слово 0000, представляющее десятичное число 0. В результате увеличения содержимое этого слова станет равным 0001, что соответствует десятичному числу 1. Продолжая последовательно увеличивать 4-битовые слова, придем к ситуации, когда, увеличивая слово 1111 (которое представляет десятичное число 15), получим в результате слово 0000, т. е. 111+1 = 0000 (15+1=0), при этом получили неверную арифметическую операцию и вернулись в исходное состояние. произошло из-за того, что слово памяти может состоять только конечного числа битов. Таким образом, числовая система ЭВМ является конечной и цикличной.

Если знаковый бит равен нулю, то значение числа легко вычисляется — игнорируется знаковый бит, а оставшиеся три бита интерпретируются как двоичный код десятичного числа. Например, слово 0110 представляет двоичное число 110, которое равно десятич­ному числу 6.

Проведение независимой экспертизы проектной документации на сайте

Источник

Представление чисел в ЭВМ

Целые числа

Для числа +1101 :

Вещественные числа (числа с плавающей точкой)

0.15625 = 00101₂
446.15625 = 110111110,00101₂ = 1,1011111000101*2 8

Знак S = 0
Порядок P = 8 + 1023 = 1031₁₀ = 10000000111₂
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE28000000000₁₆

455,375 = 111000111,0110₂ = 1,110001110110*2 8 ₂

Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101

1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881

б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011

1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818

Источник

Представление числовых данных в памяти ЭВМ

Для представления информации в памяти ЭВМ (как числовой, так и не числовой) используется двоичный способ кодирования.

Кодирование символов

Для кодирования символов достаточно одного байта. При этом можно представить 256 символов (с десятичными кодами от 0 до 255). Набор символов персональных ЭВМ, совместимых с IBM PC, чаще всего является расширением кода ASCII (American Standard Code for Information Interchange — стандартный американский код для обмена информацией). В настоящее время используются и двухбайтовые предсталения символов.

Двоично-десятичное кодирование

В некоторых случаях при представлении чисел в памяти ЭВМ используется смешанная двоично-десятичная «система счисления», где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представляются соответствующими двоичными числами от 0000 до 1001. Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18-ю значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.

Представление целых чисел в дополнительном коде

Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.

Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:

При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:

Примеры. Запишем числа, соответствующие дополнительным кодам:

Кодирование вещественных чисел

Несколько иной способ применяется для представления в памяти персонального компьютера действительных чисел. Рассмотрим представление величин с плавающей точкой.

Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double.

Как видно из таблицы, величина это типа занимает в памяти 8 байт. На рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):

Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ:

Очевидно, что более компактно полученный код стоит записать следующим образом: C073850000000000₍₁₆₎.

Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу.

Источник

Общие принципы представления информации. Числовая система ЭВМ

При работе с информацией возникает необходимость преобразования исходного представления информации, удобного для восприятия человеком, к представлению, удобному для хранения, передачи и обработки и наоборот. Такие преобразования называются кодированием и декодированием соответственно. Перечислим несколько известных систем кодирования:

Код Брайля (азбука для слепых): ;

Код морской сигнализации (морская флажковая азбука);

Двоичное кодирование: данные кодируются последовательностью 0 и 1.

С течением времени начали появляться по-настоящему сложные шифры. Один из них, употребляемый и поныне, связан с именем ученого аббата из Вюрцбурга Тритемиуса.

Клод Шеннон, ученый, заложивший основы теории информации, показал, как можно построить криптограмму, которая не поддается никакой расшифровке, если, конечно, не известен способ ее составления.

Коды, использующие два различных элементарных сигнала, называются двоичными. Удобно бывает, отвлекаясь от их физической природы, обозначать эти два сигнала символами 0 и 1. Тогда кодовые слова можно представлять как последовательности из нулей и единиц.

Последовательность битов, рассматриваемых аппаратной частью ЭВМ как единое целое, называется машинным словом.

Числовая система ЭВМ. Целые числа без знака и со знаком.

Введем основные понятия на примере 4-х битовых машинных слов. Сразу оговоримся, что такой размер слов практического интереса не представляет, однако основные закономерности сохраняют силу для машинных слов любого размера.

При последовательном увеличении 4-х битового слова 0000 на 0001 наступает ситуация, когда слово станет равным 1111 (1510). Если теперь к этому слову будет прибавлена 0001, то получим 0000, т.е. неверный результат (15+1=0) и исходное состояние. Это произошло потому, что слово памяти может состоять только из конечного числа битов. Таким образом, числовая система ЭВМ является конечной и цикличной.

Если знаковый бит = 0, то значение числа легко вычисляется (3 бита младших разрядов интерпретируются как двоичный код десятичного числа). Если знаковый бит = 1, то для оценки отрицательного числа нужно:

выполнить операцию инвертирования;

к полученному результату прибавить единицу.

3. Определите, какие отрицательные числа закодированы в словах 1011; 1100; 1001?

Индикаторы переноса и переполнения

Рассмотрим неверный арифметический результат, который возникает из-за конечной числовой системы ЭВМ.

В числовой системе без знака это будет: 1111+0001 = 0000 (15+1 = 0) возникает перенос единицы из знакового бита.

Итак, обработка числовой информации в процессоре зависит от длины машинного слова, при этом старший бит машинного слова является знаковым. Представление целых чисел в памяти ЭВМ зависит от того, сколько байт памяти отводится под целое число. Если целое число занимает 2 байта, тогда схему хранения целых чисел можно представить следующим образом:

Диапазон изменения целых чисел, которые занимают:

Отрицательные целые числа представляются в дополнительном коде (посредством операции дополнения до 2-х). Например, для 16-ти битового слова число «- 5» будет иметь код:

1111111111111011 (0000000000000101(+5) 1111111111111010 +00000000000000001 1111111111111011)

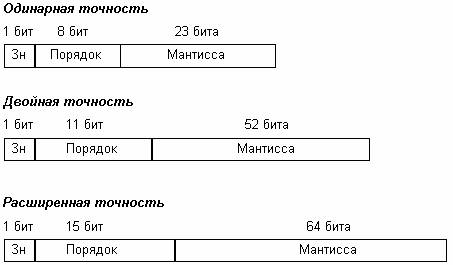
Представление вещественных чисел

Примеры. а) 372,95 = 0,37295103

б) 11010,1101 = 0,11010110125

Порядок определяет, насколько разрядов необходимо осуществить сдвиг относительно запятой. Это так называемые числа с плавающей запятой.

В памяти ЭВМ вещественные числа, приведенные к нормализованной форме, хранятся следующим образом. Для 32-х битового слова:

Порядок числа равен 128, а не 127, т.к. следует иметь в виду, что хотя для мантиссы отведены 23 разряда для одинарной точности и 55 разрядов для чисел двойной точности, в операциях участвуют 24 и 56 разрядов, т.е. имеет место скрытый разряд, который при аппаратном выполнении операций автоматически восстанавливается. Порядок числа учитывает скрытый старший разряд мантиссы.

Т.к. мантисса вещественного числа не может содержать более 7 десятичных цифр (ее мах = 8388607), компьютер при вычислениях отбрасывает лишние цифры в мантиссе, поэтому все вычисления с вещественными числами ЭВМ всегда выполняет приближенно, или с ошибкой. При более точных расчетах используются вычисления с двойной точностью. Нормализованные числа двойной точности занимают в два раза больше памяти (64 бита), под мантиссу при этом отводится 64-9 = 55 бит. В результате мантисса содержит 15 десятичных цифр. Точность расчетов возрастает в два раза.

Источник