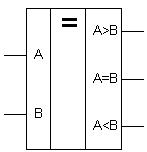
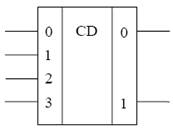
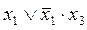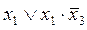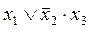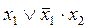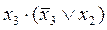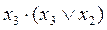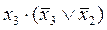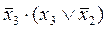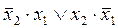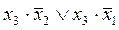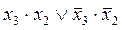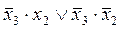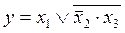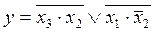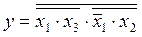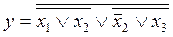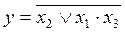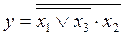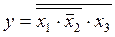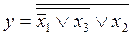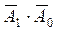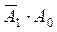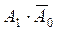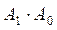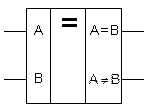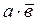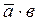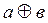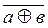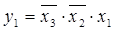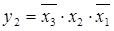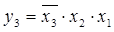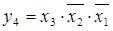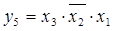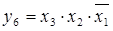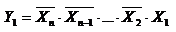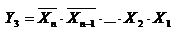укажите выходной код на выходе шифратора при шифрации десятичной цифры 7 для вашего базиса

Для реализации логической функции 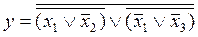с учетом инвертирования переменных потребуется _ ЛЭ 2ИЛИ-НЕ

Логическая функция _ равна х₁:

1)

2)

3)

4)

Логическая функция _ равна х₃:

1)

2)

3)

4)

1)

2)

3)

4)

Логическая функция 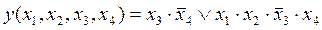записана в форме:

Логическая функция записана в форме:

Логическая функция записана в форме:

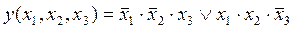
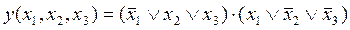
Логическая функция _ представлена в базисе «Штрих Шеффера»:

1)

2)

3)

4)

Логическая функция _ представлена в базисе «Стрелка Пирса»:

1)

2)

3)

4)

Двоичный код на выходах приоритетного шифратора «8®3», если подать «лог 1» на входы с номерами 2 и 5 одновременно, равен:

Двоичный код на выходах приоритетного шифратора «8®3», если подать «лог 1» на входы с номерами 3 и 7 одновременно, равен:

Если на входы дешифратора «3®8» с весовыми коэффициентами 4,2,1 подать соответственно сигналы х₃=1, х₂=1, х₁=0, то на выходе _ образуется минтерм :

Дешифратор «3®8» преобразует двоичный код в _ код:

Если на информационные входы D₀—D₃ и на адресные входы А₀-А₁ мультиплексора «4®1» подать «лог 1», то на выходе образуется минтерм:

1)

2)

3)

4)

Мультиплексор «2 3 ®1» должен иметь _ адресных входов:

Мультиплексор «2 3 ®1» не может использоваться для:

1) преобразования параллельного кода в последовательный

2) коммутации на выход одного из 2 3 каналов

3) формирования логической функции четырех переменных

4) дешифрации адресных входов

Демультиплексор «1®4» не может использоваться для:

1) дешифрации адресных входов

2) преобразования двоичного кода в унитарный

3) преобразования двоичного кода в код Джонсона

4) коммутации информационного входа на один из выходов

На прямом выходе А¹В одноразрядного компаратора, где А и В входы, формируется функция:

1)

2)

3)

4)

На прямом выходе А=В одноразрядного компаратора, где А и В входы, формируется функция:

1)

2)

3)

4)

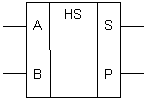
На выходе Р (переноса) одноразрядного полусумматора появляется «лог 1», если на входы А и В подаются сигналы:

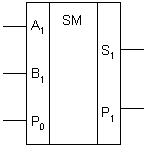
На выходах S₁ (суммы) и Р₁ (переноса) одноразрядного комбинационного сумматора появляется «лог 1», если на входы А₁, В₁ (слагаемых) и Р₀ (переноса) подаются сигналы:

При подаче на входы RS-триггера сигналов S t =1, R t =0 триггер:

Источник

Шифраторы, дешифраторы и преобразователи кодов: схемы, принцип работы

Типы логических устройств

Логические устройства разделяют на два класса: комбинационные и последовательностные.

Устройство называют комбинационным, если его выходные сигналы в некоторый момент времени однозначно определяются входными сигналами, имеющими место в этот момент времени.

Выходные сигналы последовательностных устройств определяются не только сигналами, имеющимися на входах в данный момент времени, но и состоянием элементов памяти. Таким образом, реакция последовательностного устройства на определенные входные сигналы зависит от предыстории его работы.

Что такое шифратор?

Шифратор — это комбинационное устройство, преобразующее десятичные числа в двоичную систему счисления, причем каждому входу может быть поставлено в соответствие десятичное число, а набор выходных логических сигналов соответствует определенному двоичному коду. Шифратор иногда называют «кодером» (от англ. coder) и используют, например, для перевода десятичных чисел, набранных на клавиатуре кнопочного пульта управления, в двоичные числа.

Так, для преобразования кода кнопочного пульта в четырехразрядное двоичное число достаточно использовать лишь 10 входов, в то время как полное число возможных входов будет равно 16 (n = 2 4 = 16), поэтому шифратор 10×4 (из 10 в 4) будет неполным.

Рассмотрим пример построения шифратора для преобразования десятиразрядного единичного кода (десятичных чисел от 0 до 9) в двоичный код. При этом предполагается, что сигнал, соответствующий логической единице, в каждый момент времени подается только на один вход. Условное обозначение такого шифратора и таблица соответствия кода приведены на рис. 3.35.

Используя данную таблицу соответствия, запишем логические выражения, включая в логическую сумму те входные переменные, которые соответствуют единице некоторой выходной пере­менной. Так, на выходе у₁ будет логическая «1» тогда, когда логическая «1» будет или на входе Х₁,или Х₃, или Х₅, или Х₇, или X₉, т. е. у₁ = Х₁+ Х₃+ Х₅+ Х₇+X₉

Представим на рис. 3.36 схему такого шифратора, используя элементы ИЛИ.

Источник

Шифраторы и дешифраторы

Рекомендуемые файлы

Очевидно, трудно строить шифраторы с очень большим числом входов m, поэтому они используются для преобразования в двоичную систему счисления относительно небольших десятичных чисел. Преобразование больших десятичных чисел осуществляется методами, приведенными в справочнике «Системы счисления»

Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша которой связана с определенным входом шифратора. При нажатии выбранной клавиши подается сигнал на определенный вход шифратора, и на его выходе возникает двоичное число, соответствующее выгравированному на клавише символу.

Из приведенного в табл. 5.5 соответствия десятичного и двоичного кодов следует, что переменная x₁ на выходной шине 1 имеет уровень лог. 1, если имеет этот уровень одна из входных переменных y₁, у₃, у₅, у₇, у₉. Следовательно, x₁ = y_l / y₃ / y₅ / y₇ / y₉.

Этой системе логических выражений соответствует схема на рис. 5.18,а. На рис. 5.18,б изображена схема шифратора на элементах ИЛИ-НЕ.

Шифратор построен в соответствии со следующими выражениями:

При этом шифратор имеет инверсные выходы.

При выполнении шифратора на элементах И-НЕ следует пользоваться следующей системой логических выражений:

Изложенным способом могут быть построены шифраторы, выполняющие преобразование десятичных чисел в двоичное представление с использованием любого двоичного кода,

Для обратного преобразования двоичных чисел в небольшие по значению десятичные числа используются дешифраторы (называемые также декодерами). Входы дешифратора предназначаются для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.

Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.

Дешифратор может иметь парафазные входы для подачи наряду с входными переменными их инверсий, как показано на рис. 5.19,б.

По способу построения различают линейные и прямоугольные дешифраторы.

Рассмотрим построение дешифратора, осуществляющего преобразование, заданное табл. 5.6.

Значения выходных переменных определяются следующими логическими выражениями:

В линейном дешифраторе выходные переменные формируются по (5.22) либо (5.23). При выполнении дешифратора на элементах И-НЕ пользуются (5.23), получая инверсии выходных функций. В этом случае каждой комбинации входного кода будет соответствовать уровень лог. 0 на строго определенном выходе, на остальных выходах устанавливается уровень лог. 1. На рис. 5.20 показана структура дешифратора, построенного на элементах И-НЕ, и его изображение в схемах. Структура имеет особенности, характерные для дешифраторов в интегральном исполнении:

для уменьшения числа входов формирование инверсий входных переменных осуществляется в самом дешифраторе;

подключенные непосредственно ко входам дополнительные инверторы уменьшают нагрузку со стороны дешифратора на его входные цепи.

Рассмотрим принцип построения прямоугольного дешифратора на примере дешифратора с 4 входами и 16 выходами.

Разобьем входные переменные x₈, x₄, x₂, x₁ на две группы по две переменные в каждой: x₈, x₄, и x₂, x₁. Каждую пару переменных используем в качестве входных переменных отдельного линейного дешифратора на четыре выхода, как показано на рис. 5.22,а. Выходные переменные линейных дешифраторов определяются следующими логическими выражениями:

Эти дешифраторы выполняют функции первой ступени дешифратора.

Могут быть построены прямоугольные дешифраторы с числом ступеней, большим двух.

Применение прямоугольного дешифратора может оказаться более выгодным, чем использование линейного дешифратора, в тех случаях, когда велико число входов и нежелательно использование требующихся для построения линейного дешифратора элементов с большим числом входов. Однако прохождение сигналов последовательно через несколько ступеней в прямоугольном дешифраторе приводит к большей задержке распространения сигнала в нем.

Источник

Дешифраторы и шифраторы

Практическая работа №8

Тема: Дешифраторы и шифраторы

Цель: Изучение принципа действия комбинационных схем: дешифратора, шифратора.

Вид работы: индивидуальный

Время выполнения: 4 часа.

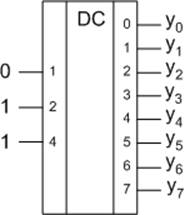
Дешифратор (декодер) – это логическая схема с несколькими входами и несколькими выходами, которая преобразует кодированные входные сигналы в кодированные выходные сигналы, причем входные и выходные коды различны. Входной код обычно имеет меньшее число разрядов, чем выходной код, и между входными и выходными кодовыми словами имеется взаимно-однозначное соответствие. При этом каждое входное слово порождает отличное от других выходное кодовое слово.

Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение на основе СДНФ:

(5)

где , — переменные с отрицанием.

По этой системе выражений строится схема требуемого дешифратора. Условное графическое обозначение такого дешифратора изображено на рис. 9.

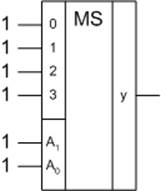
Если код на выходе устройства имеет меньшее число разрядов, чем код на входе, то это устройство обычно называют шифратором (кодером). Шифратор выполняет функцию, обратную декодеру (дешифратору), т.е. преобразует непозиционный (унитарный) двоичный 2 n разрядный код в n-разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Таблица истинности для шифратора при n = 2 приведена в таблице 6.

Система собственных функций для выходов шифратора на основе СДНФ:

, (6)

,

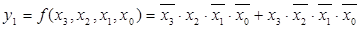
где , , , — переменные с отрицанием.

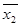
Условное графическое обозначение такого шифратора изображено на рис. 10.

Соответствующие таблице истинности ФАЛ имеют вид

(7)

.

а)

б)

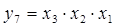
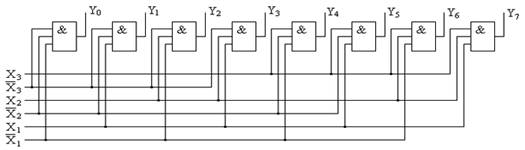
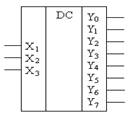
В общем случае логические уравнения для выходных переменных дешифратора n-разрядного числа имеют вид

(8)

.

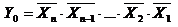
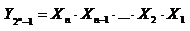
Построенные по полученным формулам дешифраторы называются линейными. К преимуществу линейных дешифраторов можно отнести высокое быстродействие, поскольку входные переменные одновременно поступают на все элементы И. Одновременно, без дополнительных задержек, формируется и результат на выходах этих элементов. Очевидно, что для реализации линейного дешифратора n-разрядного числа необходимо иметь 2 n логических элементов И с n-входами. В существующих микросхемах логических элементов количество входов ограничено. Следовательно, ограничена и разрядность реализуемых на их основе линейных дешифраторов, что является недостатком. Кроме того, недостатком является и то, что предыдущие элементы, работающие на входы дешифратора, должны иметь высокую нагрузочную способность, т.е. должны быть рассчитаны на подключение большого числа логических элементов И. Каждый из входов дешифратора подключен к 0,5·2 n логическим элементам И. Поскольку нагрузочная способность базовых логических элементов ИС не превышает величины N=10¸20, то максимальная разрядность дешифрируемых чисел для линейных дешифраторов n=4¸5.

Указанного недостатка лишены пирамидальные дешифраторы. Принцип построения этих дешифраторов состоит в том, что сначала строят линейный дешифратор для двухразрядного числа X₁, X₂, для чего необходимы 2 2 =4 двухвходовые схемы И. Далее, каждая полученная конъюнкция логически умножается на входную переменную X₃ в прямой и инверсной форме. Полученная конъюнкция снова умножается на входную переменную X₄ в прямой и инверсной форме и т.д. Наращивая, таким образом, структуру, можно построить пирамидальный дешифратор на произвольное число входов. На рис. 12 приведена структура пирамидального дешифратора для трех разрядов.

Характерным отличием пирамидальных дешифраторов от линейных является использование только двухвходовых логических элементов вне зависимости от разрядности дешифрируемого числа. В то же время количество логических элементов в пирамидальном дешифраторе больше. Однако следует иметь ввиду, что количество логических элементов, располагаемых в одном корпусе ИС, определяется главным образом, требуемым количеством выводов. Следовательно, в одном корпусе ИС можно расположить большее число двухвходовых элементов, чем трехвходовых, четырехвходовых и т.д. И значит, пирамидальная структура дешифратора по числу корпусов ИС может оказаться более предпочтительной, чем линейная.

Шифраторы выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе приводит к появлению соответствующей кодовой комбинации на выходе. Также как и дешифраторы, шифраторы бывают полными и неполными. Работа восьмивходового полного шифратора задается следующей таблицей истинности:

Источник