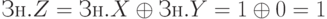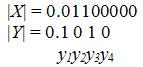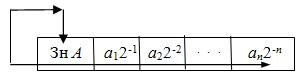умножение чисел в дополнительном коде

Умножение чисел с фиксированной запятой в прямом и дополнительном кодах

Умножение с младших разрядов множителя чисел, заданных в дополнительном коде

При умножении чисел, заданных в дополнительном коде, с младших разрядов множителя, так же как и при умножении со старших разрядов множителя в формировании произведения участвует все число, включая его знак. Произведение также получается в дополнительном коде со знаком. Соответствующая формула умножения выглядит следующим образом:

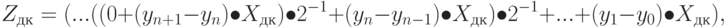( 8.4)

где y₀ – знак множителя;

y_n+1 – разряд, дополняющий множитель справа; для дополнительного кода y_n+1 ≡ 0 при любом значении знака Y_дк.

Так же, как и в предыдущем алгоритме, (y_i+1-y_i) может принимать три разных значения: (-1), (0), (+1), исходя из чего на каждом шаге вычислений к полученному на предыдущем шаге значению СЧП добавляется X_дк, ноль или (-X_дк) соответственно.

Следует отметить, что, в отличие от аналогичного способа умножения модулей сомножителей в прямом коде, здесь на последнем шаге сдвига вправо нет.

Пример 8.5.

Выполнить умножение с младших разрядов множителя следующих чисел с фиксированной запятой, заданных в дополнительном коде: X_дк = 0.1100; Y_дк = 0.0111

Решение.

Пример 8.6.

Перемножим с младших разрядов самые большие (по модулю) числа, которые можно представить в дополнительном коде: X_дк = 0.1111; Y_дк = 1.0000.

Решение.

Выполним проверку.

Это соответствует ожидаемому результату.

Выполним проверку.

Это соответствует ожидаемому результату.

Краткие итоги

В данной лекции рассмотрены способы умножения чисел с фиксированной запятой, заданных в прямом и дополнительном кодах. Рассмотрено умножение положительных и отрицательных чисел, заданных в прямом и дополнительном кодах, на 2 ±k как арифметический или логический сдвиг соответствующего числа. Показана связь различных алгоритмов умножения с используемой аппаратурой.

Источник

Умножение чисел с фиксированной запятой в прямом и дополнительном кодах

Умножение со старших разрядов множителя чисел, заданных в прямом коде

Напомним, что при реальной записи числа в памяти ЭВМ какие-либо символы, отделяющие знак от цифровой части числа, отсутствуют. Так что в данном случае мы имеем дела с пятиразрядным числом, включающим знак и четыре цифровых разряда.

Так как в прямом коде знак произведения и его модуль формируются отдельно, то следует обсудить лишь вопросы, касающиеся количества разрядов, отводимых под хранение мантисс сомножителей и мантиссы произведения.

Мы уже отмечали, что произведение следует получать в 2n-разрядной сетке, где n – количество разрядов у операндов.

Умножение со старших разрядов множителя заключается в том, что за время умножения на один разряд множителя происходит два действия:

В силу того, что в операции должны участвовать операнды одинаковой разрядности, а разрядность результата, равна 2n, то и изначально должен храниться в регистре длиной 2n, в котором младшие n позиций заполнены нулями. Также изначальное значение СЧП тоже должно быть равно нулю и изначально все ее позиции должны быть заполнены нулями. Для СЧП может быть выбран обычный регистр хранения: исходя из формулы (8.2) его значение сдвигам не подвергается.

Регистр, хранящий , в процессе выполнения умножения интересен не как единое целое, а как набор отдельных разрядов, хранящих значения y_i, использующихся при формировании очередного СЧП. Получение очередного значения y_i в следующем такте формирования СЧП может быть выполнено разнообразными схемотехничекими решениями, наиболее рациональным из которых представляется хранение в n-разрядном регистре сдвига, его сдвиге в сторону старших разрядов после анализа очередного разряда и снятии старшего разряда этого регистра в каждом такте для анализа очередного разряда y_i.

Таким образом, мы получаем следующие схемотехнические требования к регистрам, которые хранят модули операндов и результата:

Пример 8.2.

Умножить два числа с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя: X_пк = 1.0110, Y_пк = 0.1010.

Исходя из вышесказанного, выполнение данного примера будет складываться из следующих этапов.

Так как в формировании произведения участвует , сдвинутый на соответствующее число разрядов вправо, то для наглядности будем представлять его в виде отдельного столбца значений.

На основе данного примера рассмотрим еще один момент, отражающий связь между используемым при выполнении арифметических действий алгоритмом и особенностями организации ЭВМ. При умножении со старших разрядов множителя чисел, заданных в прямом коде, к значению СЧП, полученному на очередном шаге, в зависимости от значения очередного разряда y_i добавляется либо , сдвинутый на соответствующее количество разрядов вправо, либо ноль. Добавления ноля, казалось бы, только замедляет выполнение операции (в половине случаев такое сложение бессмысленно). Однако, и тот, и другой вариант действий может быть использован. Первый вариант носит название варианта без пропуска такта суммирования, а второй, соответственно, с пропуском такта суммирования.

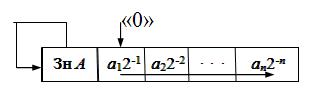
В качестве преимущества первого варианта мы отметили устранение операции суммирования с нулем, которое не приводит к изменению предыдущего значения СЧП. Но при этом у нас изменяется регулярность последовательности тактов выполнения операции умножения, а само значение y_i должно быть передано и проанализировано устройством управления компьютера, которое является сложной и нерегулярной схемой. В то же время прибавление нуля к СЧП (при y_i = 0) можно осуществить достаточно просто. Фрагмент такого действия показан на Рис. 8.6. Более подробно арифметико-логическое устройство, реализующее такой алгоритм умножения, показано в [ ].

Умножения с младших разрядов множителя чисел, заданных в прямом коде

Данное умножение реализуется согласно формуле (8.3). Суть этой формулы проста: к СЧП, полученной на предыдущем шаге добавляется , умноженный на значение соответствующего разряда y_i, а затем полученное новое значение сдвигается вправо на 1 разряд. Нюанс этого алгоритма как раз и заключается в этом сдвиге, завершающем формирование очередного значения СЧП.

Пример 8.3.

Выполнить умножение с младших разрядов множителя следующих чисел с фиксированной запятой, заданных в прямом коде:

Источник

Умножение чисел с фиксированной запятой в прямом и дополнительном кодах

Умножение чисел с фиксированной запятой имеет несколько вариантов, каждый из которых влияет на те или иные характеристики ЭВМ и, соответственно, должен быть принят во внимание при ее проектировании или анализе ее работы.

Умножение чисел c фиксированной запятой на 2 в степени ±k

Умножение двоичных чисел на целую степень числа два, казалось бы, не представляет существенных сложностей. Но при машинном выполнении этого действия необходимо учитывать ряд моментов, среди которых форма представления числа, разрядность используемой машинной сетки, код, в котором записано данное число и некоторые другие.

Данное действие используется как при выполнении операции умножения, так и деления чисел в различных кодах и с использованием разных алгоритмов.

Умножение чисел c фиксированной запятой на 2 в степени +k

Данное действие соответствует увеличению двоичного числа в k раз, что равносильно его сдвигу влево на k разрядов. При этом необходимо учесть следующие моменты:

Для положительных чисел их представление в прямом, обратном и дополнительном кодах совпадают (Рис.8.1).

Поэтому умножение числа на 2 +k для всех кодов происходит аналогичным образом. Очевидно, что для положительного числа данное действие приведет к переполнению (число превысит единицу) лишь при условии k > s.

Освобождающиеся справа разряды заполняются нулями (Рис.8.2):

Для отрицательных чисел умножения на 2 +k зависит от того, в каком коте это число представлено.

Для чисел, записанных в прямом коде, умножение не приведет к переполнению разрядной сетки в случае, если первые s разрядов числа были единицами, и выполнялось условие s > k (Рис.8.3). При этом освобождающиеся справа разряды заполняются нулями.

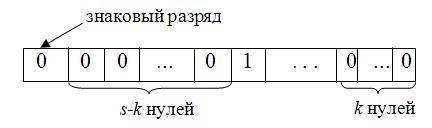
Для чисел, заданных в прямом коде, выполняется, так называемый, логический сдвиг, при котором знак числа остается на месте, а освобождающиеся за знаком позиции заполняются нулями. При этом цифры, выходящие за пределы разрядной сетки, теряются (Рис.8.4).

Цифры, выходящие за пределы разрядной сетки, теряются (Рис.8.5).

Умножение чисел, заданных в прямом коде

Рассмотрим вариант умножения операндов, представленных в прямом коде. Числа с фиксированной запятой в прямом коде записываются согласно выражению (7.1). Поэтому запишем множимое как , а множитель как . Тогда произведение нам необходимо получить в виде

и действие распадается на два самостоятельных действия: получение знака произведения и получение модуля его числовой части.

Знак произведения определяется обычным образом как сумма по модулю 2 знаков сомножителей:

( 8.1)

Теперь запишем формулу (точнее, формулы) для вычисления модуля произведения.

Преобразуя эту формулу, получим

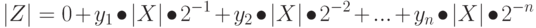( 8.2)

которая приводит к алгоритму умножения со старших разрядов множителя, или к формуле

( 8.3)

которая показывает последовательность действий при умножении с младших разрядов множителя.

Прежде чем подробно рассматривать примеры, иллюстрирующие каждый из этих алгоритмов, остановимся на некоторых общих для обоих алгоритмов моментах.

Во-первых, отметим, что мы имеем дело с двоичными числами. В связи с этим, y_i может принимать только два разных значения: «ноль» либо «единица». В первом случае величина не участвует в формировании частичного произведения на соответствующем шаге умножения, а во втором случае – участвует.

Такой сдвиг реализуется на основе сдвигового регистра (см. «Схемотехническая реализация элементов вычислительной техники» ). При этом разряды, выходящие за пределы разрядной сетки, теряются (но в полноразрядной сетке такого произойти не может).

Пример 8.1.

В-третьих, следует сказать о разрядности используемых в операции операндов, произведения и разрядной сетки, в которой необходимо проводить необходимые действия по его получению.

ЭВМ работает с операндами равной длины. Если длины операндов не совпадают, то операнд, имеющий меньшую длину, расширяется знаком до разрядности операнда с большей длиной. Поэтому будем считать, что оба операнда имеют длину в n числовых разрядов. В этом случае мы получим 2n разрядное произведение (не считая одного разряда, отводимого под знак числа).

Получение результата с точностью, превосходящей точность исходных данных, бессмысленно. В литературе показано [. ], что в случае n разрядных операндов необходимая точность получается для чисел в формате с фиксированной запятой для результата в укороченной разрядной сетке, содержащей n + d разрядов, где d ≥ log₂n.Так, для чисел, имеющих четыре разряда в цифровой части, можно проводить умножение в разрядной сетке 4 + log₂4 = 6 разрядов. Но, во-первых, это потребует проведения округления на каждом шаге вычисления произведения. А, во-вторых, возникают вопросы: «Что делать с полученным числом, которое имеет длину больше, чем длина операнда, но меньше, чем удвоенная длина операнда? Как его хранить в памяти? Как использовать в последующих операциях?» В силу этого и ряда других моментов укороченная разрядная сетка при выполнении так называемых «длинных» операций (умножения и деления) в универсальных компьютерах не применяется, и мы при рассмотрении примеров выполнения умножения и деления ею пользоваться не будем.

Источник

Умножение чисел в дополнительном коде с автоматической коррекцией

Этот алгоритм разработан Бутом и является универсальным для умножения чисел в ДК. Сомножители участвуют в операции со знаковыми разрядами, которые рассматриваются как цифровые разряды числа. Результат получается сразу в дополнительном коде со знаком.

В процессе умножения анализируются две смежные цифры множителя: та, на которую выполняется умножение в данном такте – m₁, и соседняя младшая цифра – m₂. В двоичном множителе этой паре соответствуют четыре возможных набора – «00», «01», «10», «11», каждый из которых требует выполнения следующих действий:

1. набор «01» требует сложения множимого с предыдущей суммой частичных произведений;

2. набор «10» требует вычитания множимого из предыдущей суммы частичных произведений;

3. наборы «00» и «11» не требуют ни сложения, ни вычитания, так как частичное произведение равно нулю.

В цикле умножения в каждом такте выполняются соответствующие сдвиги на один разряд. При этом могут использоваться все четыре способа умножения с некоторыми особенностями:

1. в I способе не следует выполнять последний сдвиг суммы частичных произведений;

2. в IV способе не выполняется первый сдвиг множимого.

Это объясняется тем, что в этих тактах реализуется умножение не на цифровой, а на знаковый разряд числа.

Кроме того, при выполнении алгоритма умножения с автоматической коррекцией следует помнить о правилах сдвига отрицательных чисел в ДК: при сдвиге влево освобождающиеся младшие разряды заполняются нулями, при сдвиге вправо освобождающиеся старшие разряды заполняются единицами, т.е. реализуется арифметический сдвиг числа.

С _дк = 1,101001 М = 2 6

Множитель	Множимое	Сумма ЧП	Примечания
0,1110010 0,0111001	1,111111 101001 1,111111 010010	0,000000 000000 0,000000 010111 0,000000 010111	Вычитание Сдвиги
0,0011100 0,0001110	1,111110 100100 1,111101 001000	0,000000 010111 1,111111 010010 1,111111 101001	Сложение Сдвиги Сдвиги
1,111111 101001 0,000010 111000	Вычитание
0,0000111	1,111010 010000	0,000010 100001	Сдвиги
0,0000011 0,0000001	1,110100 100000 1,101001 000000	Сдвиги Сдвиги
0,000000	1,010010 000000	0,000010 100001 1,101001 000000 1,101011 100001	Сложение Сдвиги

Ответ:

Проверка:

Устройства, которые хранят операнды, регистры, имеют следующую разрядность:

1. регистры множителя и множимого – n-разрядные;

2. регистр частичных произведений – 2n-разрядный.

Суммирование множимого следует выполнять в младшие n разрядов регистра суммы частичных произведений.

Особенность III способа умножения состоит в том, что в последнем такте не следует выполнять сдвиг в регистре сумм частичных произведений.

Алгоритм умножения двоичных чисел в ДК с простой коррекцией:

1. определить знак произведения путем сложения по модулю два знаковых разрядов сомножителей.

2. перемножить модули сомножителей, представленных в ДК, одним из четырех способов – получить псевдопроизведение.

3. если хотя бы один из сомножителей отрицателен, выполнить коррекцию по следующим правилам:

· если один сомножитель отрицателен, к псевдопроизведению прибавляется дополнительный код от модуля положительного сомножителя;

· если оба сомножителя отрицательны, к псевдопроизведению прибавляются дополнительные коды от модулей дополнительных кодов обоих сомножителей, т.е. их прямые коды.

4. Присвоить модулю произведения знак из п.1 данного алгоритма.

D _пк = 1,111001 М = 2 6

С _дк = 0,101001 – модуль множимого

D _дк = 0,000111 – модуль множителя

Знак произведения: 1 + 1 = 0

Псевдопроизведение = 0, 000100 011111

Коррекция (складываем модули операндов):

1, 010100 011111

Ответ:

Проверка:

Устройства, которые хранят операнды, регистры, имеют следующую разрядность:

1. регистр множителя – n-разрядный;

2. регистры множимого и частичных произведений – 2n-разрядный.

Первоначально множимое помещается в старшие разряды регистра, а затем в каждом такте сдвигается на один разряд вправо.

Особенность IV способа умножения состоит в том, что перед началом цикла умножения следует множимое сдвинуть на один разряд вправо.

Источник

Обратный и дополнительный коды двоичных чисел

Пример перевода
x₁=10101-[x₁]_пр=010101
x₂=-11101-[x₂]_пр=111101
x₃=0,101-[x₃]_пр=0,101
x₄=-0,111-[x₄]_пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.

3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.

Пример перевода
x₁=10101-[x₁]_доп=010101
x₂=-11101-[x₂]_обр=100010+1-[x₂]_доп=100011
x₃=0,101-[x₃]_доп=0,101
x₄=-0,111-[x₄]_обр=1,000+1-[x₄]_доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.

Источник