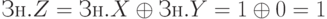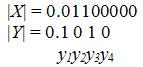умножение двоичных чисел в обратном коде
Обратный и дополнительный коды двоичных чисел
Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Двоичный калькулятор онлайн
Данный калькулятор может производить следующие действия над двоичными числами:
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 0 |
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
Пример
Для примера вычтем из числа 1011 число 101:
| − | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| + | 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 1 |
Деление двоичных чисел
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
(35 голосов, оценка: 4,69 из 5)
Умножение чисел с фиксированной запятой в прямом и дополнительном кодах
Умножение со старших разрядов множителя чисел, заданных в прямом коде
Напомним, что при реальной записи числа в памяти ЭВМ какие-либо символы, отделяющие знак от цифровой части числа, отсутствуют. Так что в данном случае мы имеем дела с пятиразрядным числом, включающим знак и четыре цифровых разряда.
Так как в прямом коде знак произведения и его модуль формируются отдельно, то следует обсудить лишь вопросы, касающиеся количества разрядов, отводимых под хранение мантисс сомножителей и мантиссы произведения.
Мы уже отмечали, что произведение следует получать в 2n-разрядной сетке, где n – количество разрядов у операндов.
Умножение со старших разрядов множителя заключается в том, что за время умножения на один разряд множителя происходит два действия:
В силу того, что в операции должны участвовать операнды одинаковой разрядности, а разрядность результата, равна 2n, то и 
изначально должен храниться в регистре длиной 2n, в котором младшие n позиций заполнены нулями. Также изначальное значение СЧП тоже должно быть равно нулю и изначально все ее позиции должны быть заполнены нулями. Для СЧП может быть выбран обычный регистр хранения: исходя из формулы (8.2) его значение сдвигам не подвергается.
Регистр, хранящий 
, в процессе выполнения умножения интересен не как единое целое, а как набор отдельных разрядов, хранящих значения yi, использующихся при формировании очередного СЧП. Получение очередного значения yi в следующем такте формирования СЧП может быть выполнено разнообразными схемотехничекими решениями, наиболее рациональным из которых представляется хранение в n-разрядном регистре сдвига, его сдвиге в сторону старших разрядов после анализа очередного разряда и снятии старшего разряда этого регистра в каждом такте для анализа очередного разряда yi.
Таким образом, мы получаем следующие схемотехнические требования к регистрам, которые хранят модули операндов и результата:
Пример 8.2.
Умножить два числа с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя: Xпк = 1.0110, Yпк = 0.1010.
Исходя из вышесказанного, выполнение данного примера будет складываться из следующих этапов.
Так как в формировании произведения участвует , сдвинутый на соответствующее число разрядов вправо, то для наглядности будем представлять его в виде отдельного столбца значений.
На основе данного примера рассмотрим еще один момент, отражающий связь между используемым при выполнении арифметических действий алгоритмом и особенностями организации ЭВМ. При умножении со старших разрядов множителя чисел, заданных в прямом коде, к значению СЧП, полученному на очередном шаге, в зависимости от значения очередного разряда yi добавляется либо , сдвинутый на соответствующее количество разрядов вправо, либо ноль. Добавления ноля, казалось бы, только замедляет выполнение операции (в половине случаев такое сложение бессмысленно). Однако, и тот, и другой вариант действий может быть использован. Первый вариант носит название варианта без пропуска такта суммирования, а второй, соответственно, с пропуском такта суммирования.
В качестве преимущества первого варианта мы отметили устранение операции суммирования с нулем, которое не приводит к изменению предыдущего значения СЧП. Но при этом у нас изменяется регулярность последовательности тактов выполнения операции умножения, а само значение yi должно быть передано и проанализировано устройством управления компьютера, которое является сложной и нерегулярной схемой. В то же время прибавление нуля к СЧП (при yi = 0) можно осуществить достаточно просто. Фрагмент такого действия показан на Рис. 8.6. Более подробно арифметико-логическое устройство, реализующее такой алгоритм умножения, показано в [ ].
Умножения с младших разрядов множителя чисел, заданных в прямом коде
Данное умножение реализуется согласно формуле (8.3). Суть этой формулы проста: к СЧП, полученной на предыдущем шаге добавляется , умноженный на значение соответствующего разряда yi, а затем полученное новое значение сдвигается вправо на 1 разряд. Нюанс этого алгоритма как раз и заключается в этом сдвиге, завершающем формирование очередного значения СЧП.
Пример 8.3.
Выполнить умножение с младших разрядов множителя следующих чисел с фиксированной запятой, заданных в прямом коде: