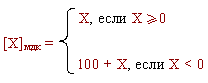вычисление в обратном коде
ЕГЭ 2019 Физика Информатика Scratch
Дневник заданий для учащихся
Прямой, обратный и дополнительные коды чисел
Представление целых чисел в компьютере.
Целые числа являются простейшими числовыми данными, с которыми оперирует ЭВМ. Для целых чисел существуют два представления: беззнаковое (только для неотрицательных целых чисел) и со знаком. Очевидно, что отрицательные числа можно представлять только в знаковом виде. Целые числа в компьютере хранятся в формате с фиксированной запятой.
Представление целых чисел в беззнаковых целых типах.
Для беззнакового представления все разряды ячейки отводятся под представление самого числа. Например, в байте (8 бит) можно представить беззнаковые числа от 0 до 255. Поэтому, если известно, что числовая величина является неотрицательной, то выгоднее рассматривать её как беззнаковую.
Представление целых чисел в знаковых целых типах.
Прямой код числа.
Дополнительный код числа.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Знаковый разряд
Возникает вопрос: с какой целью отрицательные числа записываются в виде дополнительного кода и как получить дополнительный код отрицательного числа?
Дополнительный код используется для упрощения выполнения арифметических операций. Если бы вычислительная машина работала с прямыми кодами положительных и отрицательных чисел, то при выполнении арифметических операций следовало бы выполнять ряд дополнительных действий. Например, при сложении нужно было бы проверять знаки обоих операндов и определять знак результата. Если знаки одинаковые, то вычисляется сумма операндов и ей присваивается тот же знак. Если знаки разные, то из большего по абсолютной величине числа вычитается меньшее и результату присваивается знак большего числа. То есть при таком представлении чисел (в виде только прямого кода) операция сложения реализуется через достаточно сложный алгоритм. Если же отрицательные числа представлять в виде дополнительного кода, то операция сложения, в том числе и разного знака, сводится к из поразрядному сложению.
Для компьютерного представления целых чисел обычно используется один, два или четыре байта, то есть ячейка памяти будет состоять из восьми, шестнадцати или тридцати двух разрядов соответственно.
Алгоритм получения дополнительного кода отрицательного числа.
Для получения дополнительного k-разрядного кода отрицательного числа необходимо
Можно заметить, что представление целого числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:
Отличная статья про представление чисел в памяти компьютера.
Также разработано программное решение на Паскале.
Обратный и дополнительный коды чисел
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования:
1) Разряды числа в коде жестко связаны с определенной разрядной сеткой.
1) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд.
Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Знаковым разрядомобычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Для числа +1101 прямой код 0,0001101; обратный код 0,0001101.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы
Пример. Для числа +1101:
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
| Прямой код | Обратный код | Дополнительный код |
| 1,0001101 | 1,1110010 | 1,1110011 |
Сложим числа, используя коды:
Прямой код 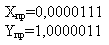 | Сложение с применением обратного кода  |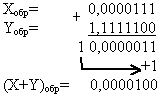
Сложение с применением дополнительного кода
Так как результат сложения является кодом положительного числа (знак 0),
Сложим числа, пользуясь правилами двоичной арифметики:
Сложим числа, используя коды:
Прямой код 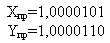 | Сложение в обратном коде  |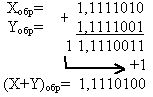
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код: (X+Y)обр=1,1110100 — из дополнительного кода (X+Y)доп=1,1110101 Дата добавления: 2015-04-21 ; просмотров: 2687 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ Модифицированные обратный и дополнительный кодыПереполнение разрядной сетки может привести к переносу единицы в знаковый разряд, что приведет к неправильному результату. Положительное число, получившееся в результате арифметической операции, может восприниматься как отрицательное, так как в знаковом разряде появится «1», и наоборот. Пример Х и Y – коды положительных чисел, но в процессе сложения в знаковом разряде появилась «1», что означает код отрицательного числа. Чтобы распознать переполнение разрядной сетки, вводятся модифицированные коды. Модифицированный обратныйкодхарактеризуется тем, что под знак числа отводится не один, а два разряда. Форма записи чисел в модифицированном обратном коде выглядит следующим образом: • для положительного числа; • для отрицательного числа В модифицированных обратном и дополнительном кодах под знак числа отводится не один, а два разряда: «00» соответствует знаку «+», «11» – знаку «-». Любая другая комбинация («01» или «10»), получившаяся в знаковых разрядах, является признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах. Пример Переполнение не наблюдается (в знаковых разрядах «00»). Результаты, полученные в обычном и модифицированном кодах, совпадают(X+ Y=1111). Задания для самостоятельной работы 1. Запишите числа X и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код. Полученный результат проверьте, используя правила двоичной арифметики. 2. Измените число Y, добавив в конец числа две единицы «11». Сложите полученные числа в модифицированном обратном и модифицированном дополнительном кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики. Контрольные вопросы 1. Что понимают под прямым кодом числа? 3. Как образуется обратный код целого отрицательного числа? 4. Каков алгоритм сложения чисел в прямом коде? 5. Каков алгоритм сложения чисел в обратном коде? 6. Чем характеризуется модифицированный обратный код? Лабораторная работа №5 Представление вещественных чисел в памяти компьютера. Арифметические операции над числами С плавающей запятой Цель работы. Изучить логические операции и основные равносильности алгебры логики, научиться составлять таблицы истинности для формул алгебры логики и преобразовывать формулы, используя основные равносильности и правила поглощения. Рассмотрим представление величин с плавающей точкой. Система вещественных чисел в математических вычислениях предполагается непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. Вследствие этого система вещественных чисел, представимых в машине, является дискретной (прерывной) и конечной. При написании вещественных чисел в программах вместо привычной запятой принято ставить точку. Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.25 в этой форме можно представить так: Если “плавающая” точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует: Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида:
Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2 k-1 – 1). Например, порядок, принимающий значения в диапазоне от –128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255. Использование смещенной формы позволяет производить операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате. Персональный компьютер позволяет работать со следующими действительными типами (диапазон значений указан по абсолютной величине): Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double. Как видно из таблицы, величина этого типа занимает в памяти 8 байт. На рисунке показано, как здесь представлены поля мантиссы и порядка:
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер 51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на положение двоичной запятой. Перед запятой должен стоять бит целой части мантиссы, но поскольку она всегда равна единице, здесь данный бит не требуется и соответствующий разряд отсутствует в памяти (но он подразумевается). Значение порядка храниться здесь не как целое число, представленное в дополнительном коде. Для упрощения вычислений и сравнения действительных чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к настоящему значению порядка, перед записью его в память, прибавляется смещение. Смещение выбирается так, чтобы минимальному значению порядка соответствовал нуль. Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ: 1. перевести модуль данного числа в двоичную систему счисления; 3. прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления; 1. Двоичная запись модуля этого числа имеет вид 100111000,0101. 3. Получаем смещенный порядок 8 + 1023 = 1031. Далее имеем 1031(10) = 10000000111(2). Очевидно, что более компактно полученный код стоит записать следующим образом: C073850000000000(16). Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу. Пример. Пусть дан код 3FEC600000000000(16) или 1. Прежде всего, замечаем, что это код положительного числа, поскольку в разряде с номером 63 записан нуль. Получим порядок этого числа. 01111111110(2) = 1022(10). Переводом в десятичную систему счисления получаем 0,88671875 1. Двоичная запись модуля этого числа имеет вид 100011,101. 3. Найдем смещенный порядок. Для этого находим смещение Очевидно, что более компактно полученный код стоит записать следующим образом: C18Е8000(16). Сначала посмотрим аналогичный пример сложения нормализованных десятичных чисел в формате с плавающей точкой (возьмем произвольные значения): Должна получиться сумма = 78.476 Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого (меньшего) числа сдвигается на три разряда вправо, порядок этого числа увеличивается на 3, получаем 0.00056*10 2 =0.056. Решение:разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо: Решение: Решение: 0.1111*2 100 / 0.101*2 11 = (0.1111 / 0.101)*2 (100-11) = 1.1* 2 1 = 0.11*2 10 Задания для самостоятельной работы Вариант 1 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 408Е130000000000; б) С077880000000000. Вариант 2 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) С075228000000000; б) 408В9В0000000000. Вариант 3 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) С07С08С000000000; б) С0811В0000000000. Вариант 4 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) С071760000000000; б) 407FF28000000000 Вариант 5 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 407С060000000000; б) С0610С0000000000 Вариант 6 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) C082B30000000000; б) С086ЕВ0000000000. Вариант7 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) С085ЕВ0000000000; б) C07D428000000000 Вариант 8 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) С07848С000000000; б) С085394000000000 Вариант 9 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) С08В794000000000; б) 407СВ28000000000. Вариант 10 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) 408ЕА14000000000; б) С07В128000000000. Вариант 11 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 40864В0000000000; б) С047140000000000. Вариант 12 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) 4060B00000000000; б) С0846С6000000000. Вариант 13 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. a) C086494000000000; 6) C083DC6000000000. Вариант 14 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) 407С360000000000; б) 408В594000000000. Вариант 15 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 4075Е28000000000; б) С07Е980000000000. Вариант 16 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) C05DCA0000000000; б) 408Е5В0000000000. Вариант 17 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 4089794000000000; б) 408В414000000000. Вариант 18 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) C057D80000000000; б) 406F0C0000000000. Вариант 19 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) 40664С0000000000; б) 40684С0000000000. Вариант 20 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. а) С088440000000000; б) С0696С0000000000. Вариант 21 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. а) С06ЕА50000000000; б) С08Е230000000000. Вариант 22 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) C0642G0000000000; 6) C082F14000000000. Вариант 23 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. a) 408B894000000000; б) С089930000000000. 4. Заданы два числа А=0.0110111*2110 и В=0.001010111*2100. Вычислить сумму, разность и произведение этих чисел. Результат привести к нормализованной форме. Вариант 24 1. Запишите код действительного числа, интерпретируя его как величину типа Single. 2. Дан код величины типа Double. Преобразуйте его в число. a) 4081C94000000000; 6) 403D800000000000. Вариант 25 1. Запишите код действительного числа, интерпретируя его как величину типа Double. 2. Дан код величины типа Double. Преобразуйте его в число. a) 408EFB0000000000; 6) 4078D28000000000. Контрольные вопросы: 1. Как получить прямой и дополнительный коды целого числа? 2. Как представляются действительные числа в памяти ЭВМ? 3. Как получить числа в нормализованной форме? 4. Как выполняются арифметические операции над нормализованными числами? Лабораторная работа №6
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Модифицированные кодыВажная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы. При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым. Рассмотрим такой пример: То есть получаем неправильный результат как по знаку, так и в цифровой части. Рассмотрим ещё один пример: Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата. Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата. Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата. Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд: » + » ставится в соответствие 00 » – » ставится в соответствие 11 Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Так как в сложении по-прежнему участвуют только числа меньше единицы, то Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда искажает младший знаковый разряд. При этом различают два типа переполнения :
|
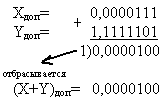
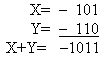
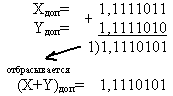
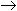(X+Y)пр=1,0001011;
