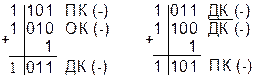вычитание чисел в дополнительном коде
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Сложение и вычитание в дополнительном коде
Прямой, обратный и дополнительный коды
В целях упрощения выполнения арифметических операций и определения знака результата применяют специальные коды для представления чисел. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства, выполняющие арифметические операции.
Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.
Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.
Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.
Прямой код
Это обычный двоичный код, рассмотренный в разделе двоичной системы счисления. Если двоичное число является положительным, то бит знака равен 0, если двоичное число отрицательное, то бит знака равен 1. Цифровые разряды прямого кода содержат модуль представляемого числа, что обеспечивает наглядность представления чисел в прямом коде (ПК).
Рассмотрим однобайтовое представление двоичного числа. Пусть это будет 28(10). В двоичном формате – 0011100(2) (при однобайтовом формате под величину числа отведено 7 разрядов). Двоичное число со знаком будет выглядеть так, как показано на рис. 2.1.
Сложение в прямом коде чисел, имеющих одинаковые знаки, достаточно просто: числа складываются, и сумме присваивается знак слагаемых. Значительно более сложным является алгебраическое сложение в прямом коде чисел с разными знаками. В этом случае приходится определять большее по модулю число, производить вычитание модулей и присваивать разности знак большего по модулю числа. Такую операцию значительно проще выполнять, используя обратный и дополнительный коды.
Обратный код
В обратном коде (ОК), так же как и в прямом коде, для обозначения знака положительного числа используется бит, равный нулю, и знака отрицательного – единица. Обратный код отрицательного двоичного числа формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. В знаковом разряде обратного кода у положительных чисел будет 0, а у отрицательных – 1.
На рис. 2.2 приведен формат однобайтового двоичного числа в обратном коде.
В общем случае ОК является дополнением модуля исходного числа до наибольшего числа без знака, помещенного в разрядную сетку.
Кроме того, в операциях сложения и вычитания требуется дополнительная операция по прибавлению бита переноса в младший разряд суммы. Рассмотрим правила алгебраического сложения в ОК (поскольку А-В=А+(-В)). Алгоритм сложения в ОК содержит:
· сложение кодов, включая знаковый разряд;
· прибавление переноса к МЗР (младшему значащему разряду) суммы.
Указанные трудности привели к тому, что в современных ЭВМ абсолютное большинство операций выполняется в дополнительном коде.
Дополнительный код
Дополнительный код (ДК) строится следующим образом. Сначала формируется обратный код (ОК), а затем к младшему разряду (МЗР) добавляют 1. При выполнении арифметических операций положительные числа представляются в прямом коде (ПК), а отрицательные числа – в ДК, причем обратный перевод ДК в ПК осуществляется аналогичными операциями в той же последовательности. На рис. 2.3 рассмотрена цепь преобразований числа из ПК в ДК и обратно в двух вариантах.
Оба способа представления чисел широко используются в ЭВМ.
Представление десятичных чисел одним полубайтом
В ЭВМ используется быстрый способ формирования ДК.При этом двоичное число просматривается от МЗР к СЗР. Пока встречаются нули, их копируют в разряды результата. Первая встретившаяся единица также копируется в соответствующий разряд, а каждый последующий бит исходного числа заменяется на противоположный (0 на 1, 1 на 0).
Видно, что результаты преобразований обоими методами совпадают.
Сложение и вычитание в дополнительном коде
При выполнении арифметических операций в современных ЭВМ используется представление положительных чисел в прямом коде (ПК), а отрицательных – в обратном (ОК) или в дополнительном (ДК) кодах. Это можно проиллюстрировать схемой на рис. 2.4.
Общее правило. При алгебраическом сложении двух двоичных чисел, представленных обратным (или дополнительным) кодом, производится арифметическое суммирование этих кодов, включая разряды знаков. При возникновении переноса из разряда знака единица переноса прибавляется к МЗР суммы кодов при использовании ОК и отбрасывается при использовании ДК. В результате получается алгебраическая сумма в обратном (или дополнительном) коде.
Рассмотрим подробнее алгебраическое сложение для случая представления отрицательных чисел в ДК.
При алгебраическом сложении чисел со знаком результатом также является число со знаком. Суммирование происходит по всем разрядам, включая знаковые, которые при этом рассматриваются как старшие. При переносе из старшего разряда единица переноса отбрасывается и возможны два варианта результата:
· знаковый разряд равен нулю: результат – положительное число в ПК;
· знаковый разряд равен единице: результат – отрицательное число в ДК.
Для определения абсолютного значения результата его необходимо инвертировать, затем прибавить единицу.
Вычитание чисел в дополнительном коде
ПРАКТИЧЕСКАЯ РАБОТА №3
Изучение принципов выполнения операций сложения и вычитания в двоичной ССЧ
Цель работы: изучить принципы выполнения операций сложения и вычитания в двоичной системе счисления.
За одно действие складываются всегда только два числа. Если нужно сложить сумму нескольких чисел, то сначала складывают первое и второе число. Затем к результату прибавляется третье число. Далее к найденному результату прибавляется четвертое число и так далее, пока не будут сложены все числа. Сложение в столбик сразу нескольких чисел, как для десятичных чисел, в двоичном счислении не принято. Принципиально это возможно, однако в процессе вычисления возникают сложности с переносом старших разрядов.
Оба складываемых числа пишутся поразрядно друг над другом. Затем складываются две цифры столбца с наименьшим разрядом. В случае переноса единица записывается в следующий столбец и учитывается при его сложении. То есть в случае переноса нужно складывать три двоичных числа. По такому алгоритму складываются столбец за столбцом справа налево, пока не будут сложены все цифры.
Правила сложения в двоичной системе:
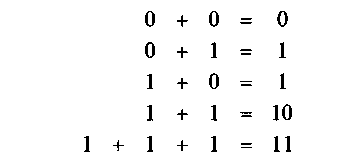 |
Арифметические действия в двоичной системе выполняют аналогично десятичной.
Рассмотрим сущность выполнения действия сложения, например, чисел 45 и 87 в десятичной системе. Сначала складываем цифры младшего разряда — пулевого, соответствующего 10° — единицам: 5 + 7 = 12. В числе 12 уже две цифры, причем цифра младшего разряда суммы — 2, а цифра 1 принадлежит более старшему разряду — первому, соответствующего 101 — десяткам. Поэтому 2 записываем, 1 — запоминаем, т.е. в младшем разряде суммы, соответствующем единицам, будет 2, а 1, соответствующую более старшему разряду — десяткам, будем учитывать при сложении цифр первого разряда. Далее складываем цифры первого разряда 4 + 8 и прибавляем к ним 1, которую запомнили; получаем 13. Теперь цифра, соответствующая первому разряду суммы — 3, а 1 переносится в старший разряд, соответствующий второму разряду суммы — 102, т.е. сотням.
Аналогично выполняется сложение в двоичной системе, например, числа «шесть» и «семь». Числа шесть и семь в двоичной системе имеют вид:
Сложение начинаем с нулевого разряда, соответствующего 2°:
0+1 = 1 (младшая цифра суммы равна 1).
Переходим к сложению цифр первого разряда, соответствующего 21 : 1 + 1 =2. Для записи числа 2 в двоичной системе требуется код: 10 (1 • 21 + 0 • 2° = 2), т.е. цифра первого разряда суммы равна 0, а 1 переносим в старший разряд (нуль записываем, один запоминаем). Таким образом, если сумма цифр больше единицы, происходит перенос в старший разряд.
Далее складываем 1 + 1 и прибавляем 1, которую запомнили, получаем 3. Число 3 в двоичной системе записываем кодом 11 (1 • 21 + 1 • 2° = 3), т.е. цифра второго разряда суммы равна 1, а старшая 1 переносится в следующий (третий) разряд.
Таким образом, сумма чисел 110 и 111 равна 1101. Нетрудно убедиться, что это двоичное число — 13 (1 • 23 + 1 • 22 + 0 • 21 + 1 • 2° = 13).
Рассмотрим теперь сущность действия вычитания в десятичной системе на примере: 132 — 87:
• сначала вычитаем цифры нулевого разряда, но так как из двух нельзя вычесть семь, занимаем 1 (один десяток — основание системы счисления) в старшем разряде, что отмечаем точкой над цифрой 3; получаем 10 + 2 = 12; 12-7 = 5;
• при вычитании цифр первого разряда необходимо занять 1 в следующем старшем разряде и, учитывая, что в первом разряде осталась цифра 2, получаем 10 + 2 — 8 = 4.
• Правила вычитания в двоичной системе:
• 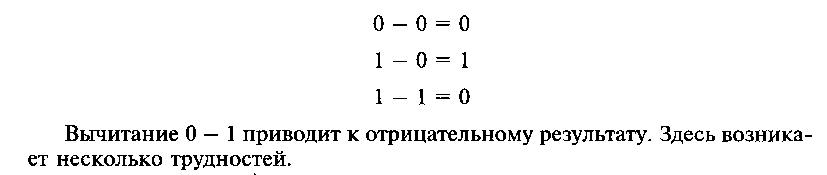 |
• Для вычитания из «0» «1» требуется занять старший разряд. 0 – 1 = 1
Аналогично выполняем вычитание из числа 1101 (13) числа 110 (6) в двоичной системе:
• первый (21) разряд: из нуля нельзя вычесть единицу, поэтому занимаем 1 (т.е. одно основание системы счисления, равное двум) и получаем 2 — 1 = 1;
• второй (22) разряд: из нуля, оставшегося после занимания единицы в этом разряде, нельзя вычесть единицу, поэтому занимаем 1 (основание, равное двум) в третьем (23) разряде: 2-1 = 1. Получим 111, т.е. двоичное число «семь».
Еще один пример вычитания:
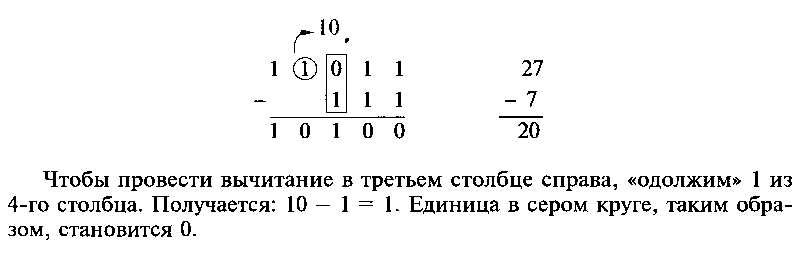 |
Вычитание чисел в дополнительном коде
В компьютерной технике вычитание производится преимущественно добавлением дополнения к вычитаемому числу.
Вычитание с дополнением также возможно в десятичной системе. Предположим, что пятиразрядный спидометр машины показывает 95000 (рис. 1). Если машина проедет еще 15 000 км, то спидометр покажет 10000. Такое же число получится, если от 95 000 отнять 85 000. Число 15 000 называется дополнением к числу 85 000. Конечно, этот способ функционирует только при выполнении условия, что при прибавлении дополнения результат не отображается в шестом разряде. То есть спидометр на рис. 1 не может быть шестиразрядным. В компьютерной технике можно просто осуществлять запрет переносов.
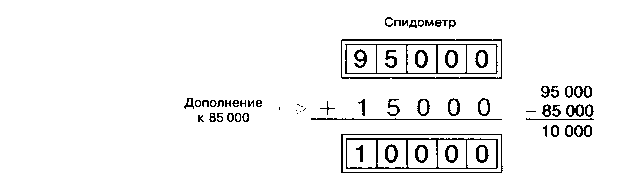 |
Рис. 1. Вычитание в дополнительном коде
Правило вычитания двоичных чисел с помощью дополнительного кода.
1. Расширить вычитаемое число до полноразрядного формата добавлением ведущих нулей
2. Инвертировать вычитаемое
3. К инверсии добавить число 1 – получим дополнение
4. Сложить уменьшаемое число и дополнение.
5. Отбросить старший разряд
| = | Уменьшаемое число | |
| — | = | Вычитаемое число |
| — | Вычитаемое число с добавлением ведущих нулей | ||||
| v | v | v | v | v | v |
| Инвертированное вычитаемое число | |||||
| + | |||||
| Дополнение | |||||
| ? | ? | ? | ? | Перенос разряда | |
| = | Уменьшаемое число | ||||
| + | Дополнение | ||||
| = | Результат |
Старший разряд отброшен.
Статьи к прочтению:
Цифровая техника — Сложение и вычитание двоичных чисел.
Похожие статьи:
Для того, чтобы вычисть числа в системе счисления с основанием q, необходимо записать одно под другим столбиком, чтобы разряды вычитаемого располагались…
Тема 3. ПРЕДОСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ Вопросы: 1. Компьютерное представление целых и вещественных чисел. 2. Арифметика двоичных чисел 2.1. Сложение в…
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода