задача о рюкзаке код c
Задача о рюкзаке
Заранее большое большое спасибо.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Задача о рюкзаке
Доброго вечера! Даны n типов предметов, каждый тип обладает своей стоимостью и весом, а также.
Задача о рюкзаке 0-1
Дарова. Я снова с вопросом по динамическому программированию. Но т.к я тупенький, то прошу.
Задача о рюкзаке
И так я все сделал как вы и просили. Условие задачи о рюкзаке: Итак, пусть у нас есть рюкзак.
Задача о рюкзаке
Условие задачи:имеются m предметов с номерами от 0 до m-1, для каждого из которых известна масса и.
Вложения
 | загрузка.rar (9.8 Кб, 16 просмотров) |
Заранее большое большое спасибо.
зы: если можно, приведите пример, при котором мой вариант решения, не будет работать 🙂
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Задача о рюкзаке 0-1
Здравствуйте! Есть задача о ранце, где даны вес и ценность каждого предмета, а также общая.

Очень прошу с помощью. Нужен код на с++, решение задачи о рюкзаке методами : динамического.
Динамическое программирование — это просто. Решаем задачу о рюкзаке
Объясняем на пальцах, как использовать приёмы динамического программирования в жизни и на работе.
Вам никогда не хотелось бросить всё и уйти из дома с одним рюкзаком? Мне да, но институт, экзамены, сессия родственники, ипотека, кот — так что не вариант.
Но если бы я собирала такой рюкзак, то положила бы в него вещи, которые можно продать побыстрее и подороже, — чтобы выручить денег для новой жизни в новом месте.
Обозначим задачу
У нас есть довольно вместительный рюкзак и дорогие вещи, которые можно в него положить. Но вот беда — лямки рюкзака выдерживают, скажем, четыре килограмма, не больше.
Нам нужно выбрать вещи наибольшей общей стоимости и не забывать про хилые лямки рюкзака.
Фулстек-разработчик. Любимый стек: Java + Angular, но в хорошей компании готова писать хоть на языке Ада.
Решаем вручную
Самый очевидный выход
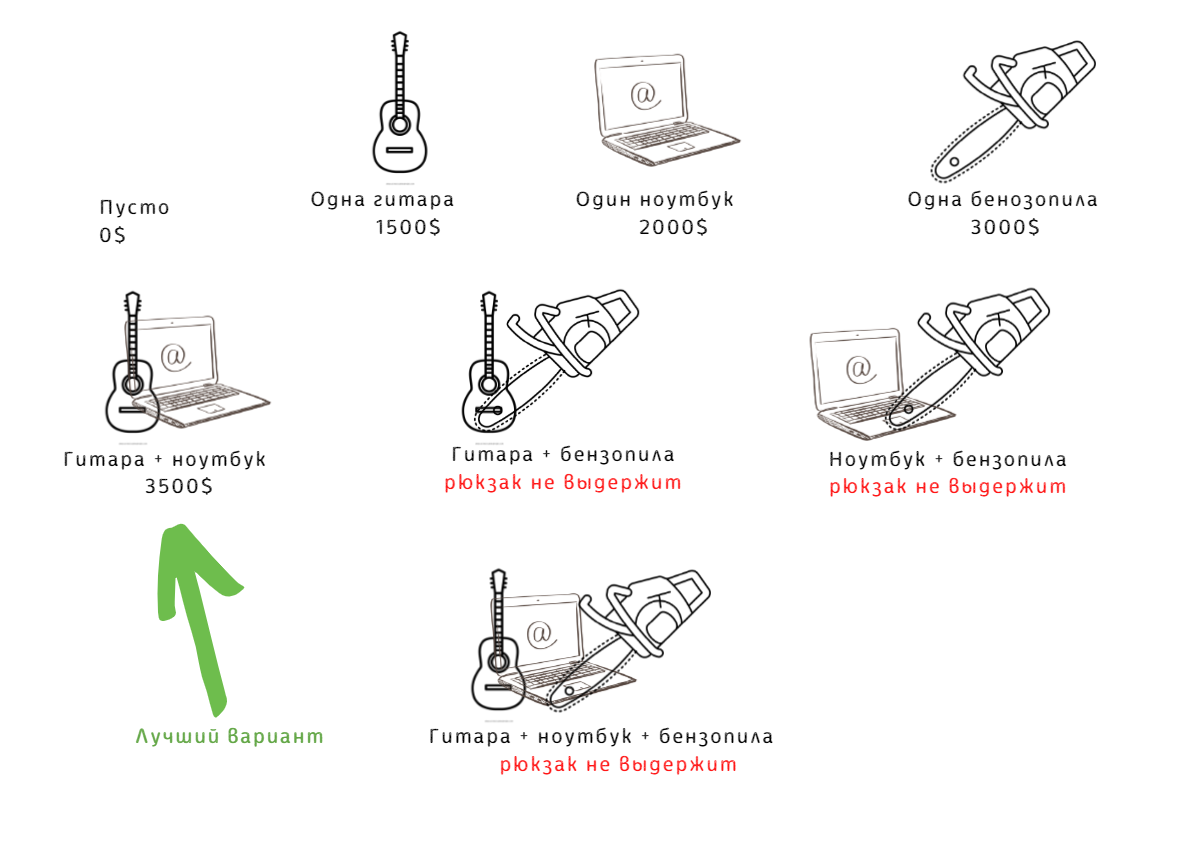
Это полный перебор, конечно! Из трёх предметов можно составить всего восемь комбинаций. Подсчитаем стоимость для каждой и выберем самый выгодный вариант:
Пока предметов только три — вполне себе годное решение, но добавим ещё один — и вариантов станет 16, а для пяти их будет уже 32.
С добавлением каждого нового предмета число комбинаций удваивается, так что сложность такого алгоритма — O(2 n ). Это медленный способ.
Приблизительное решение
Применим так называемый жадный алгоритм: на каждом шаге добавляем в рюкзак самый дорогой предмет, пока лимит веса не превышен.
В случае с нашими предметами — одним шагом дело бы и закончилось. Мы сразу же взяли бы бензопилу за 3 000 долларов, потому что она самая дорогая. А при добавлении любого нового предмета в рюкзаке уже был бы перевес.
Было ли наше решение оптимальным? Нет, потому что гитару на пару с ноутбуком наш рюкзак тоже выдержит, но стоят они 1 500 долларов + 2 000 долларов = 3 500 долларов, что больше 3 000 долларов.
Оптимальное решение
Воспользуемся приёмами динамического программирования. Разобьём задачу на подзадачи и будем последовательно их решать. При этом на каждом следующем шаге используем результаты предыдущего.
Наглядно это можно представить в виде таблицы. Её ещё называют таблицей мемоизации. Столбцы нашей соответствуют килограммам (от одного до четырёх), а строки — предметам (гитара, бензопила, ноутбук).
| 1кг | 2кг | 3кг | 4кг |
|---|---|---|---|
| гитара | |||
| бензопила | |||
| ноутбук |
Таблица до заполнения
На пересечении, в ячейках, будем записывать общую стоимость предметов в рюкзаке.
Для каждого столбца (та или иная грузоподъёмность рюкзака) нужно решить: класть гитару в рюкзак или нет.
Так как гитара весит всего один килограмм, то она влезет уже на первом шаге. Поэтому в каждой ячейке первой строки напишем 1 500 — стоимость гитары.
Мы заполнили строку целиком и узнали, что промежуточный максимум для рюкзака в четыре килограмма составляет 1500 долларов.
| 1кг | 2кг | 3кг | 4кг | |
|---|---|---|---|---|
| гитара | 1500 | 1500 | 1500 | 1500 |
| бензопила | ||||
| ноутбук |
Таблица для первого предмета — гитары
На следующем этапе рассматриваем двух кандидатов — гитару и бензопилу.
В рюкзаки, рассчитанные на один, два или три килограмма, бензопилу не положить, так что оставляем там гитару и максимум стоимости вещей 1 500 долларов. А вот для случая «четыре килограмма» обновляем максимум: кладём бензопилу стоимостью 3 000 долларов.
| 1кг | 2кг | 3кг | 4кг | |
|---|---|---|---|---|
| гитара | 1500 | 1500 | 1500 | 1500 |
| бензопила | 1500 | 1500 | 1500 | 3000 |
| ноутбук |
Таблица для двух предметов — гитары и бензопилы
Добавим последний предмет — ноутбук.
Для первых двух столбцов ничего не меняется, так как ничего, кроме гитары, в рюкзаки с грузоподъёмностью один и два килограмма положить не получится.
Зато в трёхкилограммовый рюкзак уже можно вместо гитары положить ноутбук — он дороже, обновляем максимум в этом столбце до 2 000 долларов.
Интереснее всего ситуация в последней ячейке: мы можем положить ноутбук, но он весит всего три килограмма, ещё один килограмм остаётся свободным.
И вот тут, наконец, пригодятся промежуточные результаты: мы узнали на предыдущих шагах максимальную стоимость для рюкзака, который выдерживает один килограмм, — она равна 1 500 долларов.
В итоге получаем ноутбук + гитара = 3 500 долларов, это больше предыдущего максимума в 3 000 долларов. Так что ответ в задаче — 3 500 долларов.
| 1кг | 2кг | 3кг | 4кг | |
|---|---|---|---|---|
| гитара | 1500 | 1500 | 1500 | 1500 |
| бензопила | 1500 | 1500 | 1500 | 3000 |
| ноутбук | 1500 | 1500 | 2000 | 3500 |
Таблица для всех трёх предметов
В общем случае формула для стоимости в каждой ячейке выглядит так:
S[i, j] = max (S[i−1, j], цена i-го предмета + S[i−1, j−вес i-го предмета]),
где i — номер строки, j — столбца.
То есть на каждом шаге мы выбираем между предыдущим максимумом и суммой, которую составляют стоимость текущего предмета и максимальная цена незанятого веса.
Решим на Java
Определим класс для вещей, которые можно положить в рюкзак:
Задача о рюкзаке
Доброго времени суток. Дана задача: Имеются предметы, веса которых равны w1,w2,…,wn, а цены которых равны c1,c2,…,cn. Выбрать из них предметы, суммарный вес которых меньше 20 кг, а стоимость – максимальна.
В результате работы программы должны выводиться предметы: 1, 2, 5.
Помогите разобраться, может что не так с алгоритмом поиска? Программа выводит не подходящие значения.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Задача о рюкзаке на С++
#include #include using namespace std; struct backPackItem < string.
Задача о рюкзаке
Условие задачи:имеются m предметов с номерами от 0 до m-1, для каждого из которых известна масса и.
Задача о рюкзаке 0-1
Дарова. Я снова с вопросом по динамическому программированию. Но т.к я тупенький, то прошу.
класс постановка задачи, что взять, чтобы «подороже» стырить)
Добавлено через 17 минут
итератор в функцию «Print()» может стоит добавить?
Добавлено через 4 минуты
perevertysh, stdlib.h (или cstdlib). И она уже подключена в iostream
а что если структуру для предметов создать. а то там в Print() двумерный массив без итерации.
Добавлено через 2 минуты
QuakerRUS, более того, у меня codeblocks вылетел стихийно при запуске компиляции)
Добавлено через 38 минут
Студентка-007,
вот пример с сортировкой по стоимости и весу.
Добавлено через 32 минуты
Студентка-007,
Пусть задача и решена, но вот решение на C++ кому интересно. Пусть не самое изящное (написано на коленке), но понятное с использованием лишь основных функций языка.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Задача о рюкзаке
Написать решение задачи о рюкзаке. Ёмкость рюкзака 25 кг. 12 предметов. Ценность и вес задать.

Очень прошу с помощью. Нужен код на с++, решение задачи о рюкзаке методами : динамического.
Задача о рюкзаке
И так я все сделал как вы и просили. Условие задачи о рюкзаке: Итак, пусть у нас есть рюкзак.
Задача о рюкзаке
Доброго вечера! Даны n типов предметов, каждый тип обладает своей стоимостью и весом, а также.
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Задача о рюкзаке: алгоритм, решение
Задача о рюкзаке – это одна из самых популярных задач комбинаторной оптимизации. В этой статье рассмотрим её формулировку и выполним решение одним из методов с помощью языка программирования C#.
Формулировка задачи о рюкзаке
Приведём классическую формулировку задачи о рюкзаке (задачи о ранце).
Условие: Имеется рюкзак с ограниченной вместимостью по массе; также имеется набор вещей с определенным весом и ценностью. Необходимо подобрать такой набор вещей, чтобы он помещался в рюкзаке и имел максимальную ценность (стоимость).
Алгоритм решения задачи о рюкзаке
Рассмотрим один из самых простых способов точного решения задачи о рюкзаке: это способ полного перебора.
Обозначим максимальный вес ранца, как W, а количество различных вещей N. При этом в наборе могут быть абсолютно одинаковые предметы.
Каждый предмет имеет: название, вес и стоимость (ценность):
| Название | Вес | Стоимость |
| Книга | 1 | 600 |
| Бинокль | 2 | 5000 |
| Аптечка | 4 | 1500 |
| Ноутбук | 2 | 40000 |
| Котелок | 1 | 500 |
Чтобы решить задачу, необходимо составить все комбинации наборов предметов и выбрать тот набор, масса которого не более W, а общая стоимость (по отношению к другим подходящим наборам) максимальна.
В рамках терминов комбинаторики это означает, что нужно рассмотреть все перестановки из N. Общее количество перестановок находится по формуле: N!
Если предметов пять, то придётся рассмотреть 5! = 120 различных наборов предметов.
Очевидно, что вычислительная сложность алгоритма полного перебора для решения задачи о рюкзаке равна O(N!).
Минусом способа полного перебора всех предметов, является то, что если количество вещей велико, тогда алгоритм не даст решения за приемлемое время, поскольку факториал является чрезвычайно быстро растущей функцией.
Программа, решающая задачу о рюкзаке
Перейдём к написанию кода на языке программирования C#.
Описание сущности
Сначала создадим класс Item, который реализует сущность “Предмет”. Он содержит три поля: название, вес и стоимость.
Задача о ранце и код Грея
Не так давно на Хабре была статья «Коды Грея и задачи перебора». Статья эта скорее, математическая, нежели программистская, и мне, как простому программисту, читать её было невыносимо тяжело. Но сама тема мне знакома, поэтому я решил описать её своим взглядом, а так же рассказать о том, как использовал её в решении задачи о ранце.

КДПВ: задача о ранце на живом примере
Предыстория
Всё началось 10 лет назад, когда я учился в девятом классе. Я случайно подслушал разговор учителя по информатике, рассказывающего задачку кому-то из старших: дан набор чисел, и ещё одно число — контрольное. Надо найти максимальную сумму чисел из набора, которая не превышала бы контрольное число.
Задача почему-то запала мне в душу. Вернувшись домой, я быстро накатал решение: наивный перебор всех возможных сумм с выбором наилучшего. Сочетания я получал, перебирая все N-разрядные двоичные числа и беря суммы тех исходных чисел, которым соответствуют единицы. Но я с огорчением обнаружил, что при количестве элементов начиная где-то с 30, программа работает очень долго. Оно и не удивительно, ведь время работы такого алгоритма — n*2 n (количество сочетаний, умноженное на длину суммы).
Прошло 5 лет. Я успел закончить школу и поступить в университет, но эта задача по-прежнему была со мной. Один раз, листая книгу «Алгоритмические трюки для программистов» (Hacker’s Delight / Henry S. Warren Jr.), я наткнулся на описание кода Грея: это последовательность двоичных чисел, каждое из которых отличается от предыдущего только одним битом. «Стоп!» — подумал я — «Это означает… Да! Это означает, что в той самой задаче на каждом шаге перебора можно не считать сумму целиком, а лишь добавлять или вычитать одно число». И я тут же углубился в изучение темы.
Построение кода Грея
Код Грея можно построить для числа любой разрядности. Для одного разряда он очевиден:
Чтобы добавить второй разряд, можно к этой последовательности дописать такую же задом наперёд
и ко второй половине дописать единицы:
Аналогично для трёх разрядов:
Такой код, полученный отражением кода меньшей разрядности, называется рефлексным (отражённым) кодом Грея. Бывают и другие последовательности, но на практике обычно используется именно эта.
Этот код назван в честь Фрэнка Грея, который изобрёл ламповый АЦП, выдававший цифровой сигнал именно в этом коде. При небольших изменениях уровня входного сигнала цифровой выход мог измениться только в одном бите, и этим исключались резкие скачки из-за неодновременного переключения битов.

Иллюстрация патента Фрэнка Грея
Самое наглядное применение кода Грея — в датчиках угла поворота. Датчик, аналогичный тем, что был в старых механических мышах, но определяющий не относительное смещение, а абсолютное значение угла. Для этого на каждый датчик нужно несколько оптопар и несколько щелевых решёток. Причём каждое следующее положение датчика должно отличаться от предыдущего только состоянием одного бита, иначе на границах возможно несинхронное переключение битов, и следственно — резкие скачки в показаниях прибора. Здесь видна любопытная особенность кода Грея: последнее число также отличается от первого одним битом, поэтому его можно «закольцевать».

Датчик абсолютного угла поворота. Оптические щели расположены в соответствии с кодом Грея
Применение в задаче о ранце
Но вернёмся к задаче о ранце. Стандартная формула даёт нам код Грея по номеру:
По ней мы можем только посчитать сумму все нужных элементов. А мы собирались на каждой итерации добавлять или вычитать одно значение, верно? Значит, нам нужно получить номера изменяемых битов. Для многоразрядных чисел эти номера будут такими:
Ничего не напоминает? Это номер бита, который мы устанавливаем в единицу, когда просто перечисляем обычные двоичные числа. Или иначе — номер младшей единицы в двоичном числе. Эта операция называется find first set и в большинстве процессоров существует в виде отдельной инструкции. Visual C++ предоставляет эту инструкцию в виде функции _BitScanForward.
Итак, теперь мы готовы написать программу, решающую задачу о ранце через код Грея. Сформулируем задачу так:
В файле input.txt в первой строке указана вместимость рюкзака, а в остальных строках — размеры вещей. В консоль нужно вывести максимальную загрузку рюкзака и размеры выбранных вещей. Проверку корректности ввода и пр. — нафиг.
Мы будем хранить битовую маску использованных вещей, и по мере необходимости добавлять или убирать одну из них. Чтобы обойтись int-ами, ограничим количество вещей (и используемых бит) тридцатью одной.
Прощу прощения за возможные шероховатости; к сожалению, C++ уже давно не мой профильный язык.
Работает действительно быстрее, чем сборка с нуля всех сумм, разница заметна уже при 20 числах, а при 30-и я так и не дождался выполнения наивного алгоритма, в то время как новый вариант выполняется за 7 секунд. Впрочем, учитывая экспоненциальную сложность, это совсем не мало: для 50 чисел использовать этот алгоритм уже нет смысла. К сожалению, любой точный алгоритм будет работать не быстрее, чем за 2 n ; быстрее возможно только приблизительное решение. (Апдейт: в некоторых случаях динамическое программирование и meet-in-the-middle решают задачу быстрее; подробности см. в комментариях.)
Наверное, именно поэтому я обречён до конца жизни нести свой ранец, пытаясь ускорить эту программу. Я уже однажды переписывал цикл на ассемблере, получив небольшой прирост в скорости, а сейчас даже подумываю сделать многопоточную версию программы. Вам же остаётся лишь мне посочувствовать. 🙂