записать в прямом обратном и дополнительном кодах
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Прямой, обратный и дополнительный код числа
Зачем был нужен дополнительный код?
Как получить дополнительный код?
Давайте посмотрим, как получается дополнительный код для двоичной системы счисления. Вначале зададимся разрядностью регистра, в котором будет храниться наше число. Пусть, для примера, мы будем работать с 8-ми разрядными числами. Возьмем, опять же для примера, число двенадцать и запишем его в двоичной системе счисления: 1100. Теперь впишем его в 8-ми разрядный регистр, где старшие, незадействованные в числе, разряды имеют нулевое значение (нумерация разрядов начинается с нуля).
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 12 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Такая запись соответствует 8-ми разрядному прямому коду числа двенадцать. А теперь проинвертируем все разряды регистра, т.е. заменим 0 на 1 и 1 на 0. и получим обратный код.
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 12обр | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Прибавив к числу в обратном коде единицу, получаем искомый дополнительный код.
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||||
| 12обр | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| + | 1 | ||||||||
| 12доп | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Попробуем выполнить операцию вычитания нашего числа (двенадцать) из двадцати девяти с помощью сложения. Для этого впишем двоичное представление числа двадцать девять в 8-ми разрядный регистр и прибавим к нему дополнительный код, полученный ранее из числа двенадцать. Возникающий при этом перенос из самого старшего разряда игнорируем.
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 29 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 12доп | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 17 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
Мы видим, что результирующая сумма есть двоичное число семнадцать и это действительно соответствует разности чисел двадцать девять и двенадцать.
Представление чисел с разными знаками
Идея состояла в том, чтобы хранить и обрабатывать положительные числа в прямом коде, а отрицательные в дополнительном. Необходимо было только как-то различать какое число перед нами положительное или отрицательное. Давайте, для наглядности сравним, как выглядят регистры с положительными числами и регистры с соответствующими им отрицательными числами, записанными в дополнительном коде.
| Число | Код |
| 3 | 00000011 |
| 5 | 00000101 |
| 9 | 00001001 |
| -3 | 11111101 |
| -5 | 11111011 |
| -9 | 11110111 |
Из анализа таблицы видно, что положительные числа начинаются с нулей, а отрицательные с единиц, что и позволяет в нашем примере отличать их по знаку. Но мы выбрали, для примера, небольшие положительные числа, в старшем разряде регистра которых изначально нет единицы. Но для числа «212» и соответственно «-212» это правило уже не срабатывает, так как число 212 изначально в старшем разряде регистра содержит единицу 21210 = 110101002.
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 212 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Однако, наша модель чисел с разными знаками всегда будет работать, если запретить пользоваться числами, модуль которых содержит единицу в старшем разряде регистра. Для 8-ми разрядного регистра это числа, модуль которых не превышает 127. Старший разряд регистра, при этом, просто указывает знак и поэтому, в данной модели представления чисел, его называют знаковым разрядом.
Сложение чисел с разными знаками
Переведем их модули в двоичную систему счисления и запишем в 8-ми разрядные регистры. 2110 = 101012 ; 3010 = 111102
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 30 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Чтобы получить число противоположное, по знаку, числу «30» возьмем от последнего дополнительный код. Сначала получим обратный код, инвертируя все разряды числа.
| Разр. | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 30обр | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
Теперь прибавим единицу и получим дополнительный код.
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||||
| 30обр | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| + | 1 | ||||||||
| 30доп | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 21 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 30доп | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| C | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Проанализируем полученный результат. Мы видим, что в старшем (знаковом) разряде результата содержится единица, следовательно, результат есть число отрицательное и поэтому представлено оно в дополнительном коде. Значение этого числа сразу неочевидно и чтобы понять, что это за число, нам необходимо узнать его модуль.
Из курса школьной математики известно, что модуль положительного числа есть само число, а модуль отрицательного числа есть число ему противоположное. Поэтому нам нужно получить число противоположное результату, а это мы уже знаем как сделать, нужно взять от него дополнительный код.
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Сi | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| + | 1 | ||||||||
| 9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Разр. | c | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||||
| 30доп | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 40 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Итоги, уточнеия и обобщения о кодах
| Число | Прямой код | Обратный код | Дополнительный код |
| 0 | 00000000 | 00000000 | 00000000 |
| 1 | 00000001 | 00000001 | 00000001 |
| -1 | 10000001 | 11111110 | 11111111 |
| 5 | 00000101 | 00000101 | 00000101 |
| -5 | 10000101 | 11111010 | 11111011 |
| 8 | 00001000 | 00001000 | 00001000 |
| -8 | 10001000 | 11110111 | 11111000 |
| 120 | 01111000 | 01111000 | 01111000 |
| -120 | 11111000 | 10000111 | 10001000 |
| 127 | 01111111 | 01111111 | 01111111 |
| -127 | 11111111 | 10000000 | 10000001 |
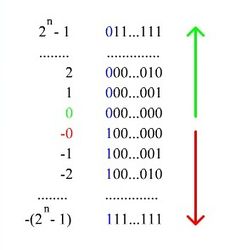
Представление целых чисел: прямой код, код со сдвигом, дополнительный код
Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:
Рассмотрим разные методы представления.
Содержание
Прямой код [ править ]
Достоинства представления чисел с помощью прямого кода [ править ]
Недостатки представления чисел с помощью прямого кода [ править ]
Из-за весьма существенных недостатков прямой код используется очень редко.
Код со сдвигом [ править ]
По сути, при таком кодировании:
Достоинства представления чисел с помощью кода со сдвигом [ править ]
Недостатки представления чисел с помощью кода со сдвигом [ править ]
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
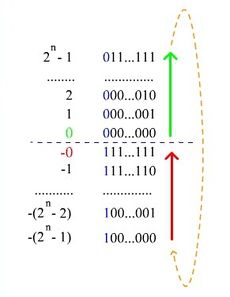
Дополнительный код (дополнение до единицы) [ править ]
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).
Алгоритм получения кода числа:
Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]
Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]
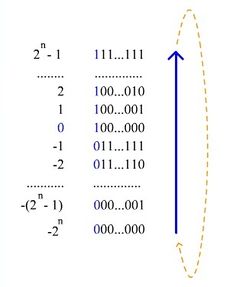
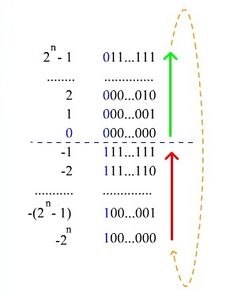
Дополнительный код (дополнение до двух) [ править ]
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).
Алгоритм получения дополнительного кода числа:
Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]
Достоинства представления чисел с помощью кода с дополнением до двух [ править ]
Недостатки представления чисел с помощью кода с дополнением до двух [ править ]
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.